Неопределенный и определенный интегралы
111-120. Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
111. 
112. 
113. 
114. 
115. 
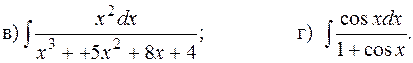
116. 
117. 
118. 
119. 
120. 
121-130. Вычислить несобственный интеграл или доказать его сходимость.
121. 
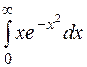. 122. 
.
123. 
. 124. 
.
125. 
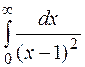. 126. 
.
127. 
. 128. 
.
129. 
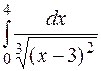. 130. 
.
131-140. Вычислить площадь области.
131. Вычислить площадь области, ограниченной лемнискатой r2=4cos2j.
132. Вычислить площадь области, ограниченной одной петлей кривой r=4sin2j.
133. Вычислить площадь области, ограниченной кривой r=2cosj.
134. Вычислить площадь области, ограниченной кривой r=cos3j.
135. Вычислить площадь области, ограниченной кардиоидой r=3(1+cosj).
136. Вычислить площадь области, ограниченной одной аркой циклоиды х=3(t-sint), y=3(1-cost), (0£t£2p).
137. Вычислить площадь фигуры, ограниченной астроидой x=cos3t, y=sin3t.
138. Вычислить площадь области, ограниченной одной петлей линии r=sin3j.
139. Вычислить площадь области, ограниченной линиями r=2cosj, r=1 (вне круга r=1).
140. Вычислить площадь области, ограниченной кардиоидой r=2(1-cosj).
141-150. Найти объем тел вращения.
141. Фигура, ограниченная одной аркой циклоиды x=2(t-sint), y=2(1-cost), вращается вокруг оси Оу. Найти объем полученного тела вращения.
142. Фигура, ограниченная линией x=acost, y=bsint, вращается вокруг оси Ох. Найти объем тела вращения.
143. Фигура, ограниченная линиями y2=2px и х=а, вращается вокруг оси Ох. Найти объем тела вращения.
144. Фигура, ограниченная линиями у2=(х-1)3 и прямой х=4, вращается вокруг оси Ох. Найти объем тела вращения.
145. Фигура, ограниченная одной аркой циклоиды x=2(t-sint), y=2(1-cost), вращается вокруг оси Ох. Найти объем тела вращения.
146. Вычислить объем тела вращения, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у=х2 и у= 
.
147. Вычислить объем тела вращения, образованного вращением вокруг оси Оу фигуры, ограниченной линиями 
148. Вычислить объем тела вращения, образованного вращением вокруг оси Ох фигуры, ограниченной линиями ху=4, у=0, х=1, х=4.
149. Вычислить объем тела вращения, образованного вращением эллипса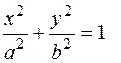 
вокруг оси Оу.
150. Вычислить объем тела вращения, образованного вращением вокруг оси Ох фигуры, ограниченной линией 
151-160. Изменить порядок интегрирования в двукратном интеграле.
151. 
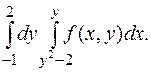152. 
153. 
154. 
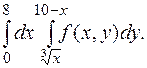
155. 
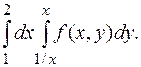156. 
157. 
158. 
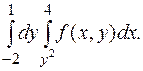
159. 
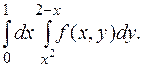160. 
161-170. Вычислить с помощью двойного интеграла объем тела, ограниченного указанными поверхностями. Сделать эскиз области интегрирования.
161. x=0; y=0; z=0; x2+y2=4, xy=z (в первом октанте).
162. x=0; y=0; z=0; х+2у=1; z=x2+y2+1.
163. y=1; z=0; x2+y2=z, y=х2.
164. x=0; y=0; z=0; x+y=1; 2x2+y2 +1=z.
165. x=1; z=0; x2-y2=z.
166. x=у; y=0; z=0; x2+z2=16.
167. y=0; z=0; x+y+z=1; 3x+y=1; 3х/2+у=1.
168. x=0; y=0; z=0; x2+y2/4=1, xy=z (в первом октанте).
169. x=0; y=0; z=0; x+y+1=z, x+y=1.
170. х=1;z=0; z=2x2-y2.
171-180. Вычислить криволинейный интеграл 1-го рода (по длине дуги).
171. 
172. 
173..
174. 
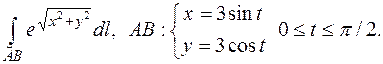
175. 
176. 
177. 
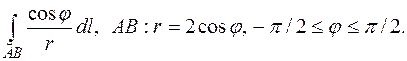
178. 
179. 
180. 
181-190. Вычислить работу силы F при перемещении вдоль линии L от точки М к точке N.
181. 
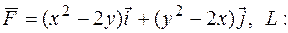отрезок MN; M(-4;0), N(0;2).
182. 
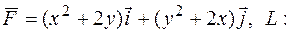отрезок MN; M(-4;0), N(0;2).
183. 
; M(-4;0), N(0;2).
184. 
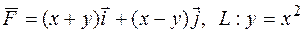; M(-1;1), N(1;1).
185. 
отрезок MN; M(-1;0), N(0;1).
186. 
отрезок MN; M(1;0), N(0;1).
187. 
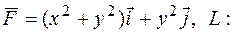отрезок MN; M(2;0), N(0;2).
188. 
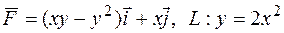; M(0;0), N(1;2).
189. 
отрезок MN; M(1;0), N(0;3).
190. 
; M(p;0), N(0;0).
191-200. Экспериментально получены пять значений функции y=f(x) при пяти значениях аргумента, которые записаны в таблице
| Х | |||||
| Y | Y1 | Y2 | Y3 | Y4 | Y5 |
Методом наименьших квадратов найти функцию вида y=ax+b, выражающую приближенно (аппроксимирующую) функцию y=f(x). Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции y=ax+b.
191. у||4,3|5,3|3,8|1,8|2,3| 196. y||3,9|4,9|3,4|1,4|1,9|
192. y||4,5|5,5|4,0|2,0|2,5| 197. y||5,2|6,2|4,7|2,7|3,2|
193. y||4,7|5,7|4,2|2,2|2,7| 198. y||5,5|6,5|5,0|3,0|3,5|
194. y||4,9|5,9|4,4|2,4|2,9| 199. y||5,7|6,7|5,2|3,2|3,7|
195. y||5,1|6,1|4,6|2,6|3,1| 200. y||5,9|6,9|5,4|3,4|3,9|
Математика: методические указания и контрольные задания для студентов первого курса заочной формы обучения всех специальностей, кроме экономических.
