М А Т Е М А Т И К А
Методические указания и контрольные задания
для студентов первого курса заочной формы обучения
всех специальностей, кроме экономических.
Издание третье, исправленное и дополненное
(II семестр)
Брянск 2007
УДК 511
Математика: методические указания и контрольные задания для студентов первого курса заочной формы обучения всех специальностей, кроме экономических. 3-е изд., исправ. и доп. (II семестр). - Брянск: БГТУ, 2007. - 18с.
Разработали: Н.А. Ольшевская, канд.техн.наук, доц.;
Н.В. Лозинская,
ст. преп.
Рекомендовано кафедрой «Высшая математика» БГТУ
(протокол № 3 от 15.11.2000г.)
ПРЕДИСЛОВИЕ
Настоящие методические указания являются продолжением аналогичных методических указаний, разработанных для студентов-заочников, по материалам первого учебного семестра. В них излагались общие рекомендации по изучению дисциплины "Математика", а также правила выполнения и оформления контрольных работ. В силу этого, в данных методических указаниях авторы на этих вопросах не останавливаются.
В течение второго учебного семестра студенты первого курса заочной формы обучения этих специальностей изучают важные разделы математики "Интегральное исчисление", по которым выполняют контрольные работы №№2,3.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Бугров, Я.С. Высшая математика: Дифференциальное и интегральное исчисление/ Я.С. Бугров, С.М. Никольский.- М.: Дрофа, 2003.
2. Бугров, Я.С. Высшая математика. Задачник/ Я.С. Бугров, С.М.Никольский. – М: Дрофа, 2004.
3. Письменный, Д.Т. Конспект лекций по высшей математике.2-е изд./ Д.Т. Письменный. -М.: Астрис-пресс, 2003-2005. – Ч.I,II.
4. Пискунов, Н.С. Дифференциальное и интегральное исчисления для втузов/ Н.С. Пискунов.– М.: Наука, 1985, - Т.1,2.
5. Данко, П.И. Высшая математика в упражнениях и задачах/П.И. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.: ОНИКС 21 век, Мир и образование, 2005. - Ч.I,II.
6. Леденева, В.К. Математика: учеб. пособ./ В.К Леденева, А.И. Гореленков, Н.В. Шарашидзе. – Брянск, БГТУ, 2006. -Ч.2.
ТЕМА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определение и свойства неопределенного интеграла
Литература. [4], гл. X, §1-3; упр. 2,5,7,9,11,14,16,17,25, 41,46, 58, 60, 66, 70 или [5], № 1315-1329.
Основные методы интегрирования
Литература. [4], гл. X, §4, упр. 27,28,33,37,47,65,72,83,89,91, 94. §6; упр. 127-131, 134,135,136,140 или [5], № 1346-1357.
Стандартные методы интегрирования
Некоторых классов функций
Литература. [4], гл. X, §5; упр. 102,105,107,110. §7-9; упр. 156,163, 164,167. §12; упр. 191-199,203,205,209,212,214. §13; [5], № 1483-1485.
Использование таблиц интегралов
Литература. [4], гл. X, §14.
Имеются элементарные функции, интегралы от которых не выражаются через элементарные функции. Примерами таких интегралов являются
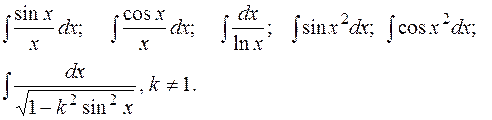
Эти и подобные интегралы определяют новые виды функций, отличных от элементарных. Многие из этих функций имеют специальные названия: функция, определяемая первым из указанных интегралов, называется интегральным синусом, вторым – интегральным косинусом, третьим – интегральным логарифмом, четвертым и пятым – интегралами Френеля и шестым (последним) – эллиптической функцией. Такие функции нашли очень широкое применение в технике, для них составлены таблицы их приближенных значений.
В о п р о с ы д л я с а м о п р о в е р к и
1. Дайте определение первообразной функции.
2. Что называется определенным интегралом?
3. Напишите таблицу основных интегралов.
4. Сформулируйте и докажите основные свойства неопределенного интеграла.
5. Сформулируйте метод замены переменной в неопределенном интеграле?
6. В чем состоит метод интегрирования по частям в неопределенном интеграле? Укажите типы интегралов, отыскание которых целесообразно осуществлять интегрированием по частям.
7. Изложите методы интегрирования простейших рациональных дробей первого, второго и третьего типов.
8. Изложите правило разложения правильной рациональной дроби на сумму простейших дробей.
9. Изложите основные методы интегрирования тригонометрических функций.
10. Изложите основные методы интегрирования иррациональных функций.






