ВВЕДЕНИЕ
Цель курсовой работы — закрепить теоретический материал, научить студентов приемам и методам познавательной деятельности, умению обобщать и вырабатывать навыки творческого мышления и самостоятельной работы.
Для расчета цепей, построения графиков и оформления отчета целесообразно применять персональные ЭВМ (ПЭВМ). При этом можно пользоваться готовыми программами систем инженерных и научных расчетов типа MATLAB, MATHCAD, MICROCAP и другими или самостоятельно написанными, что способствует закреплению навыков работы с вычислительной техникой. Умение правильно использовать компьютер становится важным показателем работы специалиста. Отсутствие у студента доступа к ЭВМ не является причиной невыполнения курсовой работы или отдельных ее пунктов.
ОПИСАНИЕ СХЕМЫ
Предметом курсовой работы является исследование электрической цепи, структурная и функциональная схемы которой
показаны на рис. 1 и 2 соответственно. Схемы активного двухполюсника — источника гармонических колебаний (ИГК), четырехполюсника и параметры их элементов выдаются преподавателем по вариантам в виде раздаточного материала.
Схема источника гармонических колебаний состоит из источников ЭДС и тока одинаковой частоты и пассивных элементов разного характера, соединенных определенным образом (см. рис. 2).
Рис. 1
Рис. 2
Роль первичной обмотки линейного трансформатора (ТР) выполняет одна из индуктивностей Ln, входящих в состав источника. При этом последовательно с индуктивностью не должен быть включен источник тока, и ток в этой ветви не равен нулю, например L 3 на рис. 2. Если в схеме нет такой индуктивности, то ее нужно создать, включив в любую ветвь без источника тока индуктивность 100 мГн и емкость 10 мкФ. Установившийся режим в схеме источника от этого не нарушится. Линейный (воздушный) трансформатор имеет две вторичные обмотки L 8 и L 9.
Напряжение u 1 вторичной обмотки L 8 ТР подается на вход повторителя, собранного на операционном усилителе (ОУ) DA1. Ориентировочные параметры такого усилителя следующие: R вх 
0,5 мОм, R вых 
100 Ом, 0 5104, f в=20 мГц, где 0 — коэффициент усиления по напряжению, а f в — верхняя рабочая частота. Часто такой ОУ используется не для получения усилительного эффекта, а для предания электрическим цепям особых свойств, получить которые без него сложно или невозможно. Для работы ОУ к нему необходимо подвести постоянное питающее напряжение U = 
10...15 В. Цепи питания на схемах обычно не изображают. 
В большинстве практических расчетов характеристики ОУ идеализируют. При этом считают, что входная проводимость и выходное сопротивление равны нулю, а коэффициент усиления имеет бесконечно большое значение. Выходное напряжение повторителя u 3 = u 1, мощность входного сигнала равна нулю, а мощность выходного может принимать любое значение в зависимости от нагрузки — это не противоречит закону сохранения энергии, так как она обеспечивается источником питающего напряжения ОУ.
Напряжение u 2 со вторичной обмотки L 9 ТР подается на инвертирующий вход компаратора — порогового элемента, преобразующего гармоническое (синусоидальное) колебание в разнополярные импульсы прямоугольной формы: U 4 = 10 В при u 2 0, U 4 = –10 В при u 2 > 0. Компаратор собран на ОУ DA2 с разомкнутой отрицательной обратной связью (ООС). В цепи без ООС коэффициент усиления ОУ оказывается чрезвычайно большим и синусоидальный сигнал преобразуется в прямоугольный. Следует обратить внимание, что напряжения u 1 и u 2 находятся в противофазе, а напряжению u 3 0 соответствует U 4 = 10 В.
Токи во вторичных обмотках трансформатора ТР для идеальных ОУ (R вх 
) равны нулю, поэтому нагрузка трансформатора никакого влияния на активный двухполюсник не оказывает.
Переключатель Кл позволяет подключить заданную схему четырехполюсника либо к выходу повторителя, либо к выходу компаратора. Переключение из одного положения в другое происходит мгновенно. В исходном (начальном) состоянии переключатель Кл находится в положении 1 (см. рис. 2). Изменение положения переключателя вызывает в схеме четырехполюсника изменение режима работы и возникновение переходного процесса.
ПРИМЕРЫ РАСЧЕТА
В учебном пособии не ставится задача проведения расчета какого-либо варианта курсовой работы. Рассматриваются отдельные фрагменты выполнения работы на примерах, позволяющих составить общее представление о характере и объеме необходимых расчетов.
Расчет источника гармонических колебаний
Пример 1. Рассчитать источник гармонических колебаний (см. п. 1.1) по схеме рис. 2, если заданы следующие исходные данные: iJ 1 = 
sin(103 t + 270) A, e 2 = 600 sin(103 t + 225) B, E 3 = 500 + j 500 B, R 1 = 0 Ом, C 2 = 20/3 мкФ, R 3 = 150 Ом, L 3 = 100 мГн, R 4 = 100 Ом, C 5 = 10 мкФ, L 6 = 100 мГн, R 7 = 20 Ом.
Решение. Предварительная подготовка схемы к расчету заключается в выборе положительных направлений токов в ветвях и их обозначении. Кроме того, необходимо обозначить все узлы схемы буквенными или цифровыми индексами. Для перехода к комплексной схеме замещения (рис. 3) все независимые источники нужно представить в комплексной форме (в виде комплексных амплитуд или комплексных действующих значений) и рассчитать комплексные сопротивления всех ветвей схемы. Так, комплексные действующие значения источников будут равны:
iJ 1 
J 1 = 4exp(j 270) = – j 4, e 2 E 2 = 
exp (j 225) = –300
– j 300, а комплексные сопротивления при w = 103 c–1: Z 1 = R 1 = 30, Z 2 = – jXC 2 = – j /(w C 2) = – j 150, Z 3 = R 3 + jXL 3 = R 3 + j w L 3 = 150 + j 100, Z 4 = R 4 = 100, Z 5 = – jXC 5 = – j /(C 5) = – j 100, Z 6 = jXL 6 = j w L 6 = j 100, Z 7 = R 7 = 20, где — символ соответствия между оригиналом и изображением функции.
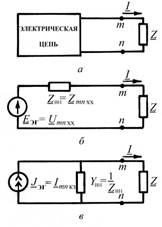
Рис.3
Рис.4
Пример 1. Рассчитать ток I 3 в первичной обмотке трансформатора (см. рис. 2) методом эквивалентного источника.
Данный метод расчета основан на теореме об эквивалентном источнике (источнике напряжения или тока) [1–4]. В соответствии с этой теоремой ток в любой ветви m – n сколь угодно сложной электрической цепи (рис. 6, а) не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником энергии, который может быть представлен последовательной (источником напряжения — рис.
6, б) или параллельной (источником тока — рис. 6, в) схемой замещения.
ЭДС идеального источника напряжения в последовательной схеме замещения должна быть равна напряжению на разомкнутых зажимах m–n схемы; ток идеального источника тока в параллельной схеме замещения равен току, протекающему между зажимами m – n, замкнутыми накоротко; внутреннее сопротивление и внутренняя проводимость эквивалентного источника должны быть равны соответственно входному сопротивлению и входной проводимости пассивной электрической цепи (источники замещены их внутренним сопротивлением) со стороны разомкнутых зажимов m–n. Эта теорема лежит в основе метода эквивалентного источника.
Решение. Расчет неизвестного тока I 3 для исходной схемы (см. рис. 3) выполним методом, например, эквивалентного источника напряжения. Найдем параметры E ЭГ и Z вн, учитывая, что обмотка трансформатора с индуктивностью L 3 =100 мГн включена между точками а–е.
А. Схема для определения E ЭГ показана на рис. 5. Направление напряжения U ae xxсовпадает с направлением неизвестного тока I 3. Из уравнения, составленного по методу контурных токов,
I 11(Z 4 + Z 5 + Z 6) – I 22 Z 6 = 0 при условии, что I 22 = J 1 = – j 4, определяем токи
I 11 = 4, I 4 = I 11 = 4, I 2 = I 22 = – j 4. Теперь из уравнения U ae xx + I 4 Z 4 + I 2 Z 2 = E 2 + E 3, составленного согласно второму закону Кирхгофа для правого контура, находим E ЭГ = U ae xx= 400 + j 400.
Рис. 5 Рис. 6
Б. Схема для определения внутреннего сопротивления генератора Z вн = Z ае вх показана на рис. 6 - здесь источники замещены их внутренним сопротивлением:
Z вн = R 3 + R 2 + Z 4 (Z 5 + Z 6) / (Z 4 + Z 5 + Z 6) = 150 – j 150.
На основании метода эквивалентного источника напряжения определяем:
I 3 = E ЭГ/(Z вн + Z L 3) = (400 + j 200)/(150 – j 150 + j 100) = 2 + j 2.
Запишем мгновенные значения тока i 3 и напряжения uL 3(t) на индуктивности L 3, представляющей собой первичную обмотку трансформатора. Комплексной амплитуде тока I 3 m = 
(2+ j 2)==4exp(j 45) соответствует мгновенное значение тока i (t)= 4 sin(103 t + 45). Комплексному действующему значению напряжения U L 3= I 3 jXL 3=(2+ j 2)(j 100)= –200+ j 200=200 
exp(j 45) соответствует мгновенное значение напряжения uL 3(t) = 400s i n(103t + 135). Кривые мгновенных значений токов i (t) или i (w t), напряжений u (t) или u (w t), построенные в декартовой системе координат (рис. 7), называются волновыми или временными диаграммами.
Рис. 7
Определим значения взаимных индуктивностей М 38 и М 39, необходимых для получения на вторичных обмотках линейного трансформатора заданных значений U 1 и U 2 (см. рис. 2). Пусть требуется получить напряжения
U 1 = 5 B, U 2 = 10 B. Так как U 1 == Xm 38 I 3 = M 38 I 3, а I 3 = 2 
, то M 38 = U 1 /(I 3) = 5/(103 2 ) = 1,25 = 1,77 мГн. При рассчитанном значении взаимной индуктивности комплексное значение напряжения на входных зажимах повторителя напряжения U 1 = jM 38 I 3 = j 103 1,25 10–3 (2 + j 2) = 5exp (j 135). (Для проверки правильности записи равенства для U 1 необходимо задаться направлением тока I 8 в L 8, записать уравнение для U 1 с учетом магнитных связей, а затем принять I 8 = 0, так как ОУ считается идеальным.) Мгновенное значение напряжения u 1 = 5 
sin (103 t + j 135). Заданный коэффициент связи позволяет определить значение индуктивности L 8 вторичной обмотки трансформатора. Так как k 38 = M 38 / 
, то, например, при k 38 = 0,5 L 8 = M 238 / / (k 238 L 3) = (1,25 
10–3)2 / (0,5210010–3) = 0,125 мГн. Аналогично: M 39 = U 2 / (I 3) = 10 / (1032 
) = 2,5 = 2,54 мГн, при k 39 = 0,5 L 9 = M 239 / (k 239 L 3) = (2,5 10–3)2 / (0,5210010–3) = 0,5 мГн, U 2 = – jM 39 I 3 = – j 103 2,5 10–3(2 + j 2) =
=10 exp(– j 45) 
u 2 = 10 
sin (103 t – j 45). Напряжение u 2 на индуктивности L 9 находится в противофазе с напряжением u 1 на L 8 (см. схему включения обмоток ТР на рис. 2).
Расчет четырехполюсника
Пример 2. Для схемы рис. 8 рассчитать токи и напряжения методом входного сопротивления, построить их векторные диаграммы. 
В схеме заданы: u вх = 40 sin(103 t +/2) B, R 1 = XC 1 =
= XC 2 = R 3 = XL 3 = 10 Ом.
Решение. Обозначим точки соединения элементов схемы и токи. Выберем условно положительные направления токов в соответствии с рис. 9. Ток в неразветвленной части схемы I 1 = U вх / Z вх, где Z вх — комплексное входное сопротивление схемы, Z вх = R 1 – jXC 1 + [– j XC 2(R 3 + j XL 3)] / [ R 3 + j (XL 3 – XC 2)] = 10 – j 10 + [– j 10(10 + j 10)] / [10 + j (10 –10)] = (20 – j 20) Ом.
Комплексное действующее значение входного напряжения U вх = j 40 B. Общий ток I 1 = j 40/(20 – j 20) = –1 + j = exp135. Токи в параллельных ветвях выразим через ток I 1: I 2 = I 1 Z 3 / (Z 2 + Z 3) =
=(–1 + j)(10 + j 10) / (– j 10 + 10 + j 10) = – 2 = 2exp(
j), I 3 = I 1 Z 2 / (Z 2 + Z 3) = (–1 + j)(– j 10) / 10 = 1 + j = = 
exp(j /4).
Построим векторную диаграмму — совокупность векторов токов или напряжений на комплексной плоскости с учетом их взаимной ориентации по фазе. Ток в неразветвленной части схемы равен геометрической сумме токов I 1 = I 2 + I 3. Векторная диаграмма токов с учетом выбранного масштаба mI = 0,5 A/см представлена на рис.9, а.
Для построения векторной диаграммы напряжений рассчитаем напряжения на отдельных элементах (участках) схемы (см. рис. 8). Направления напряжений принимаем совпадающими с направлением токов в соответствующих элементах. Рассчитаем падение напряжения на элементах схемы: UR 1 = Ued =
= R 1 I 1= 10 
и совпадает по фазе с током I 1; UC 1 = Udc = XC 1 I 1 = 10 , но отстает по фазе от тока I 1 на угол p/2; UR 3 = Ucb = R 3 I 3 = 10 и совпадает по фазе с током I 3; UL 3 = 14,1 и опережает по фазе ток I 3 на угол /2; напряжение Uca = XC 2 I 2 = 20 и отстает по фазе от тока I 2 на угол /2.
Рис. 8 Рис. 9
Геометрическая сумма U R 1 + U C 1 + U R 3 + U L 3 = U вх = U ea, а сумма U R 3 + U L 3 равна по модулю падению напряжения на емкости С 2 — Uca. Кроме того, эта векторная сумма равна выходному напряжению четырехполюсника.
Векторная диаграмма напряжений показана на рис.9, б (mU = 8 B/см). Мгновенные значения тока i 1 и выходного напряжения u вых: I 1 = exp(j 3 /4) i 1 = 2 sin(103 t + 3/4), U вых = j 20 u вых =
= 20 sin(103 t + p/2).!4283?> D075 <564C 2KE>4=K< 8 2E>дным напряжениями
j = y2KE – y2E = p/2 _ p/2 = 0, 0 >B=>H5=85 459Aтвующих значений U вых / U вх = 20/40 = 0,5.
