Линейное программирование
Постановка задачи линейного программирования.
Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
В 1939 году Леонид Витальевич Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом, были заложены основы линейного программирования. Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование. Термин «программирование» нужно понимать в смысле «планирования» (один из переводов англ. programming). Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, ещё до того, как компьютеры были использованы для решения линейных задач оптимизации.
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
 (1)
(1)
при условиях
 (2)
(2)
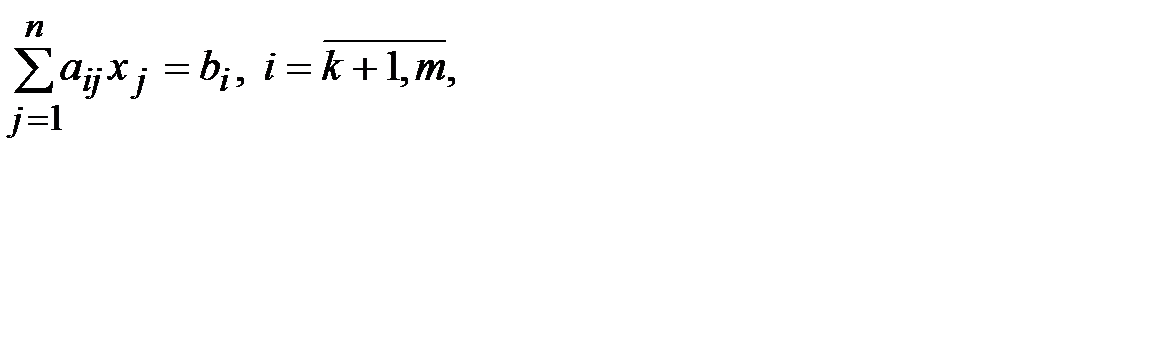 (3)
(3)
 (4)
(4)
Функция (1) называется целевой функцией (или линейной формой) задачи (1) – (4), а условия (2) – (4) – ограничениями данной задачи.
2. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального для «≤» (минимального для «≥») значения функции (1) при выполнении условий (2) и (4), где k = m, s = n.
3. Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции (1) при выполнении условий (3) и (4), где k = 0, s = n.
Формы записи задачи линейного программирования
Различают три основные формы задач линейного программирование в зависимости от наличия ограничений разного типа:
a) Стандартная задача линейного программирования
max(


 (5)
(5)

 …,
…, 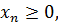
или, в матричной записи,
max <c, x>
Ax ≤ b, x ≥ 0, (6)
где  —матрица коэффициентов. Вектор c называется вектором коэффициентов линейной формы, b — вектором ограничений.
—матрица коэффициентов. Вектор c называется вектором коэффициентов линейной формы, b — вектором ограничений.
Стандартная задача важна ввиду наличия большого числа прикладных моделей, сводящихся наиболее естественным образом к этому классу задач линейного программирования.






