1) Предел суммы
Предел суммы равен сумме пределов, если каждый из них существует, т.е.
2) Предел разности
Предел разности равен разности пределов, если каждый из них существует, т.е.
3) Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
4) Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
5) Предел произведения
Предел произведения равен произведению пределов, если каждый из них существует, т.е.
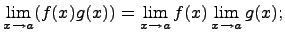
6) Предел частного
Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.
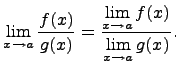
7) Предел степенной функции
где степень p - действительное число.
8) Предел показательной функции
где основание b > 0.
9) Предел логарифмической функции
где основание b > 0.
10) Теорема "о двух милиционерах"
Предположим, что $ g(x)\leqs f(x)\leqs h(x)$ для всех x близких к a, за исключением, быть может, самой точки x = a. Тогда, если
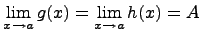то 
То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу A.
Первый замечательный предел: 
Непрерывность функции в точке. Непрерывность элементарных функций.
Функция y=f(x) называется непрерывной, в точке x0, если выполняются 3 условия:
1) Она определена в некоторой окрестности в точке х0
2) Существует lim f(x)=A при х->х0
3) f(x0)=A
Если ни одно из этих условий не выполняется, функция называется разрывной в точке х0
Функция называется непрерывной на открытом интервале, если она непрерывна в каждой точке этого интервала.
lim (delta y)=0 при (delta x ->0) – основное свойство непрерывности функции.
Если функция непрерывна в точке х0, то малому приращению аргумента соответствует малое приращение функции.
Функция называется непрерывной на замкнутом интервале, если
1) 1)Она непрерывна на открытом интервале
2) 2)Непрерывна слева в точке В и непрерывна справа в точке А
Функция непрерывна слева в точке х0, если:
1) определена в некоторой левой полу окрестности
2) существует lim f(x)=A при x->x0-0
3) A=f(x0)
Аналог даётся непрерывности справа.
Классификация точек разрыва функции
1) Если выполняется 1 и 2 условие непрерывности функции в точке, а 3 не выполняется, то точка х0 называется точкой устранимого разрыва.
2) Если функция разрывна в точке х0, но lim f(x)=A при x->x0-0, lim f(x)=B при x->x0+0 и А не равно В, то х0 называется точкой конечного скачка или точкой разрыва первого рода.
Теоремы Коши
1. Пусть функция непрерывна на замкнутом интервале [a,b] и на концах этого интервала принимает разные по знаку значения. f(A)*f(B)<0. Тогда внутри этого интервала найдётся такая точка С принадлежащая (a,b), что f(C)=0
2. Функция непрерывная на замкнутом интервале [А,В] принимает своё наибольшее и наименьшее значение
3. Функция непрерывная на замкнутом интервале принимает все значения между наибольшим и наименьшим.
