Задание.
Рассчитать комплексным методом все токи и напряжения в электрической цепи, схема которой с заданными параметрами приведена ниже.
Изобразить RLC -схему цепи согласно заданным комплексным сопротивлениям ветвей.
Построить векторную диаграмму токов и напряжений на комплексной плоскости и проверить с её помощью выполнение законов Кирхгофа.
Определить комплексную мощность цепи и проверить выполнение балансов активной и реактивной мощностей цепи.
Записать мгновенные значения всех токов и напряжений.
Исходные данные.
| Z1 |
| Z2 |
| Z3 |
| Z4 |
| Z5 |
;
;
;
;
;
.
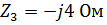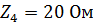Решение.
Подготовим цепь к расчету комплексным методом: обозначим условные положительные направления токов в ветвях, напряжений на элементах:
| I |
| I2 |
| I3 |
| U |
| Z1 |
| Z2 |
| Z3 |
| Z4 |
| Z5 |
| I4 |
| I5 |
| U2 |
| U4 |
| U5 |
| U1 |
| U3 |
Рассчитаем токи и напряжения в ветвях схемы:
;
;
;
;
;
;
;
;
.
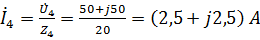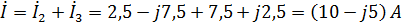Согласно заданным комплексным сопротивлениям ветвей изобразим RLC -схему данной цепи:
| L5 |
| L2 |
| R4 |
| R5 |
| R1 |
| C3 |
| C1 |
;
;
;
;
.
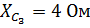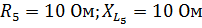Построим векторную диаграмму токов и напряжений на комплексной плоскости:
Пунктирные линии на диаграмме показывают выполнение законов Кирхгофа.
Определим комплексную мощность цепи и проверим выполнение балансов активной и реактивной мощностей:
а) Комплексная мощность цепи:
;
.
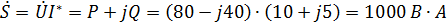б) Для активной мощности:
;
.
в) Для реактивной мощности:
.
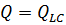Запишем мгновенные значения токов и напряжений:
Для тока 
;
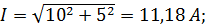
Аналогично для остальных токов:
Для напряжения 
;
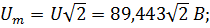
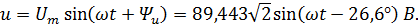
Аналогично для остальных напряжений:
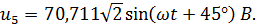
Расчет сложной цепи разными методами.
Задание.
В заданной схеме цепи значения активных и реактивных сопротивлений определены при некоторой круговой частоте ω синусоидального тока.
Рассчитать комплексы токов всех ветвей:
– методом контурных токов;
– методом узловых напряжений.
Рассчитать ток одной из ветвей методом эквивалентного генератора.
Проверить выполнение баланса активной мощности и баланса реактивной мощности цепи.
Определить напряжение между точками A и B, отмеченными на схеме цепи.
Записать мгновенные значения токов ветвей.
Исходные данные.
| L1 |
| E1 |
| E2 |
| L3 |
| L4 |
| L5 |
| R5 |
| R6 |
| C6 |
| A |
| B |
.
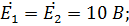
Решение.
а) Рассчитаем комплексы токов всех ветвей методом контурных токов (МКТ).
| L1 |
| E1 |
| E2 |
| L3 |
| L4 |
| L5 |
| R5 |
| R6 |
| C6 |
| A |
| B |
| I2 |
| I3 |
| I4 |
| I5 |
| I1 |
| I6 |
| Ik1 |
| Ik2 |
| Ik3 |
Составим систему уравнений по второму закону Кирхгофа относительно контурных токов:
;
.
Подставляя числовые значения сопротивлений и ЭДС, получаем следующую систему уравнений:
.
Решением данной системы являются контурные токи. Найдем их:
Определим токи в ветвях схемы:
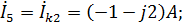
б) Подтвердим правильность решения проверкой баланса активной мощности и баланса реактивной мощности в цепи.
Комплексная мощность источников:
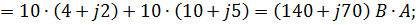
Активная мощность приемников:
баланс сходится.
Реактивная можность приемников:
=2∙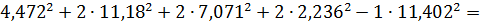 
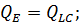,баланс сходится.
в) Определим напряжение между точками A и В.
Проверим по другому контуру:
г) Рассчитаем комплексы токов всех ветвей методом узловых напряжений (МУН).
Подготавливаем схему к расчету по МУН. Обозначим условные положительные направления токов в ветвях, номера узлов (т.к в схеме имеется ветвь, содержащая только идеальный источник ЭДС(z2=0), в качестве опорного выберем один из узлов этой ветви), направления узловых напряжений:
| L1 |
| E1 |
| E2 |
| L3 |
| L4 |
| L5 |
| R5 |
| R6 |
| C6 |
| I2 |
| I3 |
| I4 |
| I5 |
| I1 |
| I6 |
| U10 |
| U20 |
| U30 |
Т.к сопротивление второй ветви данной схемы равно 0, то очевидно: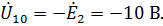 
Запишем систему уравнений для неизвестных узловых напряжений второго и третьего узлов:
;
.
Подставляя числовые значения проводимостей и узловых токов, получаем следующую систему уравнений:
Решением данной системы являются неизвестные узловые напряжения. Найдем их:
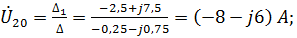
Определим токи в ветвях схемы:
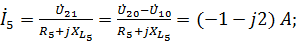
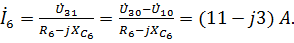
Полученные значения токов совпадают с расчетом по МКТ.
д) Найдем ток в первой ветви схемы методом эквивалентного генератора (МЭГ).
В соответствии с МЭГ, ветвь с искомым током выделяется, а оставшаяся часть схемы заменяется эквивалентным генератором с ЭДС E ЭГ, численно равной напряжению на зажимах выделенной ветви и сопротивлением ZЭГ, равным входному сопротивлению относительно зажимов выделенной ветви.
Обозначим узлы первой ветви a и b, тогда получаем схему расчета по МЭГ:
| I1 |
| a |
| L1 |
| E1 |
| b |
| EЭГ |
| ZЭГ |
| L5 |
| ZЭ1 |
| ZЭ2 |
| a |
| b |
| Zвх |
| a |
| b |
| L3 |
| L4 |
| R5 |
| R6 |
| C6 |
| a |
| b |
| L5 |
| E2 |
| L4 |
| R5 |
| R6 |
| C6 |
| I2 |
| I’3 |
| I’4 |
| a |
| b |
| L3 |
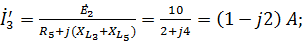
Из схемы расчета по МЭГ находим ток в первой ветви:
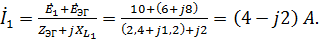
Полученное значение совпадает с расчетами по МКТ и МУП.
е) Запишем мгновенные значения токов ветвей.
Для тока 
;
Аналогично для остальных токов:
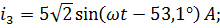
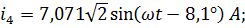
Библиографический список.
1. К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. Теоретические основы электротехники, т. 1. – 4-е изд., СПб.: Питер, 2003. – 463 с.
2. Практикум по ТОЭ, ч. 1. Под ред. проф. М.А. Шакирова. СПб.: Изд-во Политехн. ун-та, 2006. – 252 с.
3. А.Б. Новгородцев. Расчет электрических цепей в MATLAB: Учебный курс. – СПб.: Питер, 2004. – 250 с.
