Задание.
Определить магнитный поток, индукцию, напряженность и объемную плотность энергии магнитного поля во всех участках магнитопровода данной магнитной цепи. Потоками рассеяния пренебречь.
Рассчитать собственные индуктивности катушек, взаимную индуктивность, коэффициент магнитной связи между катушками и коэффициент рассеяния. Объяснить, почему значение взаимной индуктивности катушек не может превышать среднего геометрического значений их индуктивностей.
Найти силу, действующую между полюсами сердечника.
Исходные данные.
| w1 |
| a |
| b |
| d |
| ∆2 |
| a |
| w2 |
| b |
;
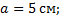
| w1 |
;
;
;
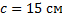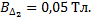
Решение.
| ∆2 |
| w2 |
| w1 |
| lср1 |
| lср2 |
| lср3 |
| 5 |
| 5 |
| 10 |
| 10 |
| 10 |
| i1 |
| i2 |
Обозначим выбор среднего значения длины каждого участка l ср k магнитопровода, размеры в сантиметрах:
Определим магнитные сопротивления для каждого участка магнитопровода:
;
;
.
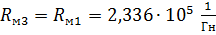| Rм1 |
| F1 |
| Ф1 |
| I |
| II |
| Ф2 |
| Ф3 |
| Rм2 |
| Rм3 |
| F2 |
.
Для полученной схемы запишем уравнения по законам Кирхгофа:
Решая данную систему, находим 
:
;
;
Рассчитаем магнитную индукцию и напряженность на каждом участке магнитной цепи:
;
;
;
.
Найдем объемную плотность энергии на каждом участке:
;
;
;
.
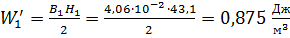Определим индуктивности обмоток L1 и L2, взаимную индуктивность M:
а)
| Rм1 |
| F1 |
| Ф1 |
| Ф2 |
| Ф3 |
| Rм2 |
| Rм3 |
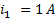, по второй 
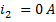. Схема замещения в этом случае будет иметь вид:
Определим потоки в первом и втором стержнях, используя эквивалентные преобразования и закон Ома:
;
Определяем собственную и взаимную индуктивность:
;
.
б)
| Rм1 |
| F2 |
| Ф1 |
| Ф2 |
| Ф3 |
| Rм2 |
| Rм3 |
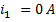, по второй 
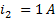. Схема замещения в этом случае будет иметь вид:
Определим потоки в первом и втором стержнях, используя эквивалентные преобразования и закон Ома:
;
;
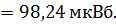
Определяем собственную и взаимную индуктивность:
;
.
Определим коэффициент магнитной связи между обмотками:
Определим коэффициент рассеяния:
.
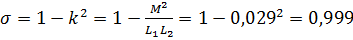Определим силу, действующую между полюсами сердечника:
Покажем, что значение взаимной индуктивности катушек, не может превышать среднего геометрического их индуктивностей:
(*)
;
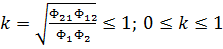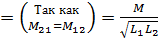ЧАСТЬ III. РАСЧЕТ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ УСТАНОВИВШЕМСЯ
СИНУСОИДАЛЬНОМ ТОКЕ.
Расчет простой цепи с помощью векторной диаграммы.
Задание.
Построить векторные диаграммы токов и напряжений для цепи, схема которой и некоторые известные параметры приведены ниже.
Определить указанные величины, используя векторные диаграммы.
Проверить решение, применяя комплексный метод.
Исходные данные.
| L3 |
| I |
| I2 |
| R2 |
| С1 |
| С2 |
| I3 |
| U |
| UC1 |
| UC2 |
| UL3 |
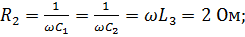
Искомые величины: U, I, P.
Решение.
Зададим условные положительные направления токов в ветвях и напряжений на элементах:
| L3 |
| I |
| I2 |
| R2 |
| С1 |
| С2 |
| I3 |
| U |
| UC1 |
| UC2 |
| UL3 |
Исходные данные позволяют сразу строить качественную векторную диаграмму по следующему алгоритму:
1. 
2. 
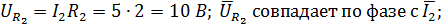
3. 
; из диаграммы: 
4. 
5. 
6. 
7. 
Найдем активную мощность P:
Проверим выполнение условий баланса для активной и реактивной мощностей, выполнение соотношения полной мощности:
а) Для активной мощности:
.
б) Для реактивной мощности:
вар;
в) Для полной мощности:
| L3 |
| I |
| I2 |
| R2 |
| С1 |
| С2 |
| I3 |
| U |
Из диаграммы:
.
Рассчитаем входное сопротивление цепи:
Определим токи:
Полученные результаты согласуются с векторной диаграммой.
