ЧАСТЬ I. РАСЧЕТ ПОЛЯ В ЭЛЕКТРОСТАТИЧЕСКОЙ СИСТЕМЕ И ЕЕ ХАРАКТЕРИСТИК.
Задание:
Дан бесконечно длинный проводящий цилиндр радиусом R1, окруженный двумя слоями диэлектрика с диэлектрическими проницаемостями ε1 и ε2. Граница раздела диэлектриков представляет собой цилиндрическую поверхность радиусом R2.
В зависимости от расстояния r между осью цилиндра и произвольной точкой найти электрическое смещение D, напряженность E, поляризованность P, потенциал U и плотность энергии 
электрического поля. Построить зависимости D=D(r), E=E(r), P=P(r), U=U(r).
Определить:
- энергию электрического поля Wэ1, заключенную в области диэлектрика с ε1;
- обобщенную силу, действующую на поверхность цилиндра 
на единицу осевой длины;
- емкость цилиндра относительно проводящей цилиндрической оболочки радиусом 
на единицу осевой длины.
Исходные данные:
| R2 |
| R1 |
| ε1 |
| ε2 |
Решение:
1. Разделим рисунок на три области:
0: 0≤r≤R1
1: R1≤r≤R2
2: R2≤r≤R3
2. Найдем 
для каждой из областей:
2.1. 0: 0≤r≤R1
В области цилиндра поля нет, следовательно:
2.2. 1: R1≤r≤R2
Используем постулат Максвелла:
Имеем: 
Отсюда: 
Рассчитаем τ по заданным параметрам:
Так как 
следовательно:
;
Так как 
.
Отсюда: 
= 
.
2.3. 2: R2≤r≤R3
Аналогично области 1 получаем: 
, 
;
= 
.
3. Приняв 
, найдем 
для каждой из областей:
3.1 
;
Так как поля внутри цилиндра нет, то 
, получаем:
= 
.
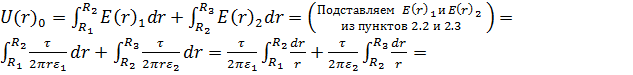
3.2 
.
3.3 
.
4. Найдем энергию электрического поля Wэ1, заключенную в области диэлектрика с ε1:
4.1 Найдем 
.
4.2 Найдем 
:
.
5. Найдем обобщенную силу, действующую на поверхность цилиндра на единицу осевой длины:
Так как 
, получаем:
6. Найдем емкость цилиндра относительно проводящей цилиндрической оболочки радиусом на единицу осевой длины:
| U1 |
| U2 |
| R3=2 R2 |
| R2 |
| R1 |
7. Полученные результаты:
7.1 
в зависимости от области:
0: 
.
1: 
.
2: , 
7.2 Плотность энергии электрического поля:
.
7.3 Энергию электрического поля Wэ1, заключенная в области диэлектрика с ε1:
.
7.4 Обобщенная сила 
, действующая на поверхность цилиндра:
.
7.5 Емкость цилиндра относительно проводящей цилиндрической оболочки радиусом :
8. Графики зависимостей:
| R1 |
| R2 |
| R3 |
| R1 |
| R2 |
| R3 |
ЧАСТЬ II. РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО
ТОКА С ПОМОЩЬЮ ЗАКОНА ОМА
И ЗАКОНОВ КИРХГОФА.
Расчет входного сопротивления электрической цепи и токов во всех ветвях при подключении цепи к источнику э.д.с.
Задание.
Определить входное сопротивление цепи постоянного тока со стороны полюсов b и c при замкнутом и разомкнутом положениях ключа. Сопротивления всех резисторов Rk = 10 Ом.
Найти токи во всех ветвях схемы при подключении цепи к источнику напряжения U = 100 В.
Рассчитать напряжение между зажимами a и c.
Исходные данные.
| a |
| b |
| c |
Rk = 10 Ом.
U = 100 В.
Решение.
а) Ключ разомкнут:
| b |
| I1 |
| I2 |
| I3 |
| I4 |
| R2 |
| R1 |
| R3 |
| R4 |
| c |
| d |
| b |
| I1 |
| I2 |
| I3 |
| I4 |
| R2 |
| R1 |
| R3 |
| R4 |
| c |
| d |
| Схема 1a |
| b |
| I1 |
| I2 |
| R2 |
| R1 |
| Rэ1 |
| c |
| d |
| Схема 2a |
.
| Rэ2 |
| b |
| I1 |
| I2 |
| R1 |
| c |
| Схема 3a |
.
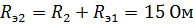| b |
| Rвх |
| c |
| Схема 4a |
| Iвх |
| Uвх |
Найдем токи в ветвях схемы:
Из схемы 4а:
.
Из схемы 3а:
.
.
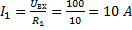Из схемы 2а:
.
Из схемы 1а:
.
Найдем напряжение между зажимами a и c:
Так как на участке ab ток равен 0, то 
.
б) Ключ замкнут:
Изобразим схему при замкнутом ключе, зададим условные положительные направления токов в ветвях:
| a |
| b |
| c |
| d |
| e |
| I1 |
| I2 |
| I3 |
| I4 |
| R2 |
| R1 |
| R3 |
| R4 |
| I5 |
| I6 |
| I7 |
| R5 |
| R6 |
| R8 |
| R7 |
| R9 |
Представим схему в удобном для расчета виде:
| I5 |
| I6 |
| R5 |
| R6 |
| b |
| I1 |
| I2 |
| I3 |
| I4 |
| R2 |
| R1 |
| R3 |
| R4 |
| c |
| d |
| Схема 1б |
| a |
| R8 |
| R7 |
| R9 |
| I7 |
| e |
| Rэ2 |
| b |
| I1 |
| I2 |
| R2 |
| R1 |
| Rэ1 |
| c |
| d |
| Схема 2б |
| a |
| R8 |
| R7 |
| R9 |
| I7 |
| e |
;
.
| b |
| I1 |
| I2 |
| R1 |
| Rэ4 |
| c |
| Схема 3б |
| Rэ3 |
| I7 |
;
.
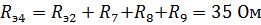| b |
| Rвх |
| c |
| Схема 5б |
| Iвх |
| Uвх |
| b |
| I1 |
| Iэ5 |
| R1 |
| c |
| Схема 4б |
| Rэ5 |
.
Найдем токи в ветвях схемы:
Из схемы 5б:
.
Из схемы 3б:
;
;
.
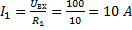Из схемы 2б:
;
.
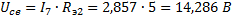Из схемы 1б:
;
.
Найдем напряжение между зажимами a и c:
Из схемы 2б:
.
Расчет сложной электрической цепи.
Задание.
Найти токи и напряжения ветвей в электрической цепи постоянного тока.
Проверить условие баланса мощности в цепи.
Определить напряжение между отмеченными на схеме точками A и B.
Исходные данные.
| В |
| А |
| R1 |
| R3 |
| R2 |
| R4 |
| Е1 |
| Е3 |
| Е4 |
| J |
.
Решение.
| В |
| А |
| R1 |
| R3 |
| R2 |
| R4 |
| Е1 |
| Е3 |
| Е4 |
| J |
| J |
| I1 |
| I2 |
| I3 |
| I4 |
| I |
| II |
Запишем уравнения по первому закону Кирхгофа для 1 и 2 узлов:
.
Запишем уравнения по второму закону Кирхгофа для I и II контуров:
.
Подставляя числовые данные, получаем следующую систему уравнений:
.
Корнями уравнений системы являются искомые токи. Решим ее и найдем их:
;
;
;
;
;
;
;
;
;
.
Определим напряжения в ветвях схемы:
;
;
;
.
Проверим условие баланса мощности в цепи:
;
;
;
;
;
;
, Баланс сходится.
Определим напряжение между точками А и В:
.
Для проверки определим напряжение между точками А и В по другому контуру:
.
