Ћ = k/n – относительная частота появления события А, где k – число появлений события а в n испытаниях.
0,999 – (например) абсолютная частота
Ћ = k/n = X/n - число появлений события а в n испытаниях.
M[h] = M[X/n] = 1/n*np=p
D[h] = D[X/n] = 1/n2*D[X]= 1/n2*npq=pq/n
Ћ = k/n = X/n = X1/n + … + Xn/n~N(p, pq/n)
№10.Вероятность в непрерывных пространствах эл событий и ее св-ва. Геометрические вер-ти.
Пусть 
- непрерывное простр-во.
Алгебра событий (F) – это система подмножеств W, W={ω1,,ω2,…} кот.удовл-ет следующим свойствам: 1. ΩÎF, ÆÏF; 2. A,BÎF => A+B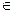 
F, ABÎF, не А и не ВÎ F; 3. F 
явл-ся сигма-алгебро й, если определены операции. Для счетного числа событий.
Пусть событие А 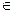F, тогда Р(А) -вероятность, число, которое должно удовл-ть:
1.P(Ω)=1; 2.АÎВ,Р(А)≥0; 3.А∙В≠0, A+BÎF=>P(A+B)=P(A)+P(B).
=ÆÞ 
Свойства вероятностей: 1.Р(Æ)=0 -вер-ть невозможного события 2. 
3. АÌВ- если А-следствие В, то Р(А)<=Р(В). 4. P(A+B)<=P(A)+P(B) 5. непрерывности: если
А1ÌА2Ì…ÌАnÌ…,то 
;
если А1ÉА2É…ÉАnÉ…, то 
Геометрические вер-ти, Для любого подмножества А можно посчитать его площадь: Р(А)=площ.А/площ.Ω. Т.к. вер-ть пропорцион-на площади, то чем > лощадь, тем > вероятность попадания в событие. P(A)=mes(A)/mes(Ω) – мера А/мераS.
14.Мат. ожидание и дисперсия суммы случайных величин .
M[X]=mx= 
M[Y]=my= 
(M[X], M[Y])-центр распределения.Пусть X и Y - случ. вел. С конечными мат. ожиданиями. Мат. ожидание их суммы равно сумме их мат. ожиданий. M[X+Y]=
M[X]+M[Y] Пусть X и Y- взаимно независимые случ. вел с конечными мат. ожиданиями. Мат ожидание произведения XY равно произведению их мат. ожиданий. M[XY]= 
=M[X]*M[Y].
Это правило распространяется на любое конечное число взаимно независимых случ. величин. Заметим, то последнее равенство для зависимых случ. величин, вообще говоря, е выполняется. Пусть X и Y- случ. Вел с совместным распределением, задаваемым таблицей (1). Условное мат. ожидание случ. dел. X при условии, что Y принимает заданное значение Y = yj, вычисляется по формуле: M[X/Y=yj]=
Дисперсия суммы случайных величин: D[X+Y] z=X+Y => D[z]=M[(z-mz)2], а mz=mx+my
D[z]= M[((X-mx)+(Y-my))2]= M[(X-mx)2]+2 M[(X-mx)(Y-my)]+
+M[(Y-my)2]=D[X]+2cov(X,Y)+D[Y]
Таким образом: D[X±Y]=D[X]+D[Y]±2cov(X,Y) Если X и Y независимые, то cov(X,Y)=0 => D[X±Y]=D[X]+D[Y] Рассмотрим D[aX±bY]=a2D[X]+b2D[Y]±2abcov(X,Y)
Числовые характеристики: 1. Мат ожидание: 
т. ожиданий. M{} т. ожиданий. M{}2.Дисперсия
Св-ва:
M[X+Y]=M[X]+M[Y] M[X*Y]=M[X]*M[Y], если X и Y независимые D[X+Y]]=D[X]+D[Y], если X и Y независимые
3.Ковариация
4.Коэффициент корреляции
(Св-ва ковариации билет 13, св-ва корреляции билет 15)
№17.Нормальный закон на плоскости.
Двумерное нормальное распределение –это распределение системы двух случайных величин (X,Y) с плотностью распределения f(x,y), определяемой формулой.
Плотность распределения случ. вел X, f1(x), вычисляется интегрированием f(x,y) по y:
Аналогично вычисляется плотность распред случ вел Y,f2(y):
Формула (1) показывает,что в случае двумерного нормального распределения с плотностью (1) компоненты X и Y имеют нормальное распред, причем M[X]=m1, D[X]=σ12, M[Y]= m2, D[Y]=σ22
Ковариация X и Y равна
cov(X,Y)=M[(X-m1)(Y-m2)]= = 
Отсюда следует,что параметр ρ в (1) есть коэффициент корреляции
Св-ва:
1.Если (X,Y) имеет норм. распред.:
Каждая компоненты этого распределения также имеет нормал. распределение
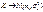
2. Если ρ=0 => f(x,y)= f1(x) ´ f2(x) => X и Y – независимые
3.Условная плотность распределения:
f(X/y) и f(Y/x) – нормальные плотности
Геометрически плотность f(x,y) двуменого нормального распределения (1) представляет «холмообразную» поверхность. Проекция вершины холма на плоскость xOy имеет координаты (m1, m2) Эта точка называется центром рассеивания.
Сечение поверхности Z=f(x,y) плоскостями, параллельными плоскости xOy, есть кривые, определяемые ур-нием:
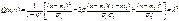, где λ – const. Проекциями этих кривых на плоскость xOyбудут эллипсы. Т.к. плотность f(x,y) имеет на этих кривых постоянное значение, то соответствующие эллипмсы наз. э ллипсами равных вероятностей
