Пусть X1…Xn… - независимые и одинаково распределенные случайные величины с мат.ожиданием miи дисперсией si2. Среднее арифметическое их: 
]=nm/n=n
.
При n->∞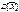 
-> 0. Среднее арифметическое можно представить: 
, т.е. можно рассмотреть как сумму случайных величин. Тогда
– в силу центральной предельной теоремы
Теорема Муавра-Лапласа.
Пусть Х – случайная величина, имеющая биномиальное распределение. (q=1-p; n испытаний)
Х – число успехов в n испытаниях по схеме Бернулли
Х=0…n
Введем величину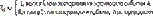 
Причем P[Xi=1]=p M[Xi]=1*p+0*q=p
P[Xi=0]=qD[Xi]=M[Xi2]-p2=p-p2=p(1-p)=pq
X = X1 + … + Xn (они все независимы и имеют одинаковое распределение)
M[X] = M[X1 + … + Xn] = M[X1] + … + M[Xn] = np
D[X] = D[X1 + … + Xn] = D[X1] + … + D[Xn] = npq
Следовательно: X~N(np,npq)
Теорема Муавра-Лапласа позволяет количественно оценить разброс события А в некотором эксперименте, который может повторятся n раз в неизменных условиях. Приблизительное значение p равно значению наблюдаемой относительной частоты появления события А в n экспериментах, причем, чем больше n тем выше относительная точность этого результата.
№22. Теорема Чебышева и ее обобщение.
Если дисперсии n-независимых случайных величин (X1…Xn) ограничены одной и той же постоянной, то при неограниченном увеличении числа n среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.
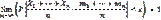
Док-во:
По условию: M(X1)=m1… M(Xn)=mn
По первому неравенству Чебышева получаем:
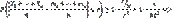
поскольку P>1, то:
Вывод: при достаточно больших n выполнение рассматриваемого неравенства является событием практически достоверным, а неравенства противоположного смысла практически невозможно.
Таким образом предел по вероятности следует понимать не как категорическое отверждение, а как утверждение, вероятность которого гарантируется с вероятностью близкой к 1 (при n->∞)
Таким образом, при большом числе случайных величин практически достоверно, что их средняя случайная величина как угодна мало отличается от неслучаной – среднего математического ожидания, т.е. перестает быть случайной.
Этим заключением обоснован выбор средней арифметической в качестве меры истинного значения мат. ожидания.
Практическое значение:
Пример: Необходимо установить размер страхового взноса, с условием что он(?) сделает выплаты при наступлении страхового случая. Замечание Если все измерения проводятся с одинаковой точностью и дисперсией (D[Xi]=s2), то дисперсия их средней величины
Т.е. средний разброс случайной величины 
меньше разброса каждого измерения. Увеличивая число измерения можно уменьшить влияния случайных погрешностей (но не систематических)
№23. Асимптотическое распределение среднего арифметического независимых случайных величин и относительной частоты.
