Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два типа нелинейных регрессионных моделей:
1. регрессии нелинейные относительно включенной факторной переменой, но линейные по парметрам:
-полином порядка n: y=a+b1x+b2x2+..+bnxn+ε;
-гипербола: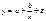 
2. регрессии нелинейные по параметрам:
-степенная функция: y=axbε,
-показ. функция: y=abxε,
-экпонен. функция: y=ea+bxε.
В первом случае для оценки параметров применяется МНК, т.к. эти функции линейны по параметрам. Например, для параболы второй степени: y=a+b1x+b2x2+ε необходимо произвести замену переменных: х=х1, х2=х2, тогда получим двухфакторное уравнение регрессии: y=a+b1x1+b2x2+ε для оценки которого используется МНК. Во втором случае нелинейных моделей по параметрам различают два вида нелинейных моделей:
-нелинейные модели внутренне линейные,
-нелинейные модели внутренне нелинейные.
Если нелинейная модель внутренне линейна, то она может быть сведена к линейному виду. Если нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции.
Линеаризация – математическое преобразование нелинейной зависимости в линейную.
Примеры линеаризации:
1. степенная функция: y=axbε,
Логарифмируем: lny=lna+blnx+lnε
{∑lny=nlna+b∑lnx
{∑lny*lnx=lna∑lnx+b∑(lnx)2
a и b находим методом МНК.
2. обратная функция: y=1/(a+bx+ε).
Линеаризуем путем обращения уравнения относительно переменной 1/у.
1/у=a+bx+ε.
3. логистическая функция: y=a/(1+be-cx+ε)
Обращая обе части равенства получаем:
1+be-cx+ε=a/y, вычитаем 1 получаем be-cx+ε=а/у-1
Далее логарифмируем по основанию е:
Lnb-cx+ε=ln(a/y-1), проведя замены получим:
Z=B-cx+ε.
Внутренне нелинейные по параметрам модели нельзя линеаризовать, поэтому их относят к нелинейным.
№. Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.
индекс корреляции (R):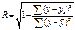 
Величина данного показателя находится в границах: 0 ≤ R ≤ 1, чем ближе к 1, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
индекс детерминации используется для проверки существенности в целом ур-ия нелинейной регрессии по F- критерию Фишера:
, где R2- индекс детерминации, n- число наблюдений, m – число параметров при переменной х.
Ранжирование факторов, участвующих во множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии, с помощью частных коэффициентов корреляции — для линейных связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции.
Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
Частные коэффициенты корреляции, измеряющие влияние на у фактора хi при неизменном уровне др. факторов можно определить по формуле:
; 
При двух факторах и i=1 данная формула примет вид:
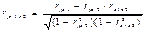
Частные коэффициенты корреляции изменяются в пределах от -1 до 1.
Множест коэфф корреляции явл показателем тесноты связи оценивающим совместное влияние всех факторных признаков на результативный.
Качество регрессионной модели оценивают с пом множ коэф детерминации.
у него 2 свойства
