При отклонениях исследуемой зависимости от линейного вида для оценки корреляционной зависимости используют корреляционное отношение. Пусть даны сгруппированные данные по признакам х и у.
| X1 | X2 | …. | Xs | |
| Y1 | n11 | n21 | … | n1s |
| Y2 | n21 | n22 | … | n2s |
| …. | …. | …. | … | … |
| Yk | nk1 | nk2 | … | nks |
| Yсред. | y1сред | y2сред | … | ysсред |
Каждая группа содержит те значения у, которые соответствуют опред. значению х. nij-число значений уi наблюдаемых при уровне хj, тогда групповая средняя равна:
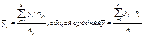
Групповая дисперсия отражает случайную вариацию, т.е. часть вариации происходящую под влиянием неучтенных факторов. Групповая дисперсия – это дисперсия значений признака, принадлежащих группе, относительно групповой средней: 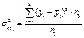 Внутригрупповая дисперсия – это средняя арифметическая групповых дисперсий, взвешенная по объемам групп:
Внутригрупповая дисперсия – это средняя арифметическая групповых дисперсий, взвешенная по объемам групп: 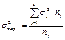 Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающего под влиянием группировочного признака. Межгрупповая дисперсия – дисперсия групповых средних относительно общей средней:
Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающего под влиянием группировочного признака. Межгрупповая дисперсия – дисперсия групповых средних относительно общей средней: 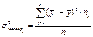 Теорема: если совокупность состоит из нескольких групп, то общая дисперсия равна сумме дисперсий:
Теорема: если совокупность состоит из нескольких групп, то общая дисперсия равна сумме дисперсий: 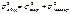 Корреляционное отношение есть квадратный корень отношения межгрупповой и общей дисперсий:
Корреляционное отношение есть квадратный корень отношения межгрупповой и общей дисперсий:
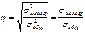
Свойства корреляционного отношения:
1) 0≤η≤1
2) Если η=0, то у и х не связаны
3) Если η=1, то связь функциональная
4) η≥IrI
5) Если η=IrI то имеет место точная линейная корреляционная зависимость.
№6. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. После того как найдены оценки коэффициента корреляции, детерминации и параметров уравнения регрессии, необходимо провести оценку их значимости, а также проверить свойства данных, выполнение которых предполагалось при оценивании уравнения. Проверка статистического качества уравнения регрессии состоит из следующих элементов:
1) проверка гипотезы о статической значимости коэффициента корреляции.
2) проверка гипотезы о статической значимости каждого коэффициента уравнения
3) проверка гипотезы о статистической значимости уравнения регрессии в целом. При этом выдвигается нулевая гипотеза, что коэффициент корреляции равен нулю, т. е. r = 0, и следовательно, фактор х не оказывает влияния на результат у. F-отношения (F-критерий): 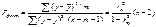
Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение,чтобы факторная дисперсия превышала остаточную в несколько раз. Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место прислучайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл
Оценка стат. значимости параметров регрессии проводится с помощью t – статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Рассчитываются стандартные ошибки параметров знач. t – критерия Стьюдента.
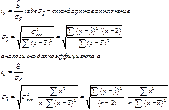
Оценка значимости аналогична рассмотренной выше для коэффициента корреляции.
№19. Ошибки спецификации уравнения регрессии. Спецификация регрессии – отбор факторных переменных, включаемых в регрессионную модель и определение формы модели.
Гипотеза о статистической значимости оценок может быть правильной и неправильной, поэтому возникает необходимость ее проверки. В результате статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух типов.
Ошибка первого рода состоит в том, что будет опровергнута правильная гипотеза. Обычно ее называют уровнем значимости α – т.е. вероятность совершить ошибку первого рода. Обычно уровень значимости α принимают равным 0,05 или 0,01 (например если α=0,05 то в 5 случаях из 100 имеется риск допустить ошибку первого рода).
Ошибка второго рода состоит в том что будет принята неправильная гипотеза. Число степеней свободы ν=n-k-1, где n-число наблюдений (объем выборки), k-число параметров при факторных переменных в уравнении регрессии (для однофакторной регрессии k=1 и ν=n-2).  — случайная величина, характеризующая отклонения реального значения результативного признака от теоретического.
— случайная величина, характеризующая отклонения реального значения результативного признака от теоретического.
Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака  подходят к фактическим данным у.
подходят к фактическим данным у.
К ошибкам спецификации относятся неправильный выбор той или иной математической функции для 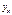 , и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.
, и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.




