ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ ФИЛЬТРАЦИИ
НЕФТИ, ГАЗА И ВОДЫ.
Особенности фильтрации. Характеристики пористой среды.
Фильтрацией называется движение жидкостей, газов и их смесей в пористых и трещиноватых средах, т.е. в твердых телах, пронизанных системой сообщающихся между собой пор и микротрещин.
В отличие от движения жидкости по трубам фильтрации присущи следующие основные особенности:
- чрезвычайно малые размеры поровых каналов;
- крайне низкие скорости движения жидкостей;
- исключительно большая роль сил трения вследствие вязкости жидкостей, огромных поверхностей поровых каналов и их шероховатости.
Одной из основных характеристик пористой среды служит коэффициент пористости.
Коэффициентом пористости называется отношение объема пор ко всему объему пористой среды:
.
Под пористостью в теории фильтрации понимается эффективная (активная) пористость, учитывающая только те поры и микротрещины, которые соединены между собой и через которые может фильтроваться жидкость.
Скоростью фильтрации называется отношение объемного расхода (дебита) жидкости или газа к общей площади поперечного сечения образца породы:
.
По-другому V - это фиктивная скорость, т.е. скорость, с которой двигалась бы жидкость, если бы пористая среда отсутствовала (m =1).
Средняя величина скорости фильтрации в сечении F совпадает с истинной скоростью в тех случаях, когда скорость фильтрации не меняется по сечению пласта. В общем случае в различных точках сечения F скорость фильтрации может быть неодинакова. Тогда истинное значение скорости фильтрации в любой точке пласта определится соотношением:
,
где dQ - величина объемного расхода жидкости сквозь проходящую через данную точку элементарную площадку dF, нормальную к направлению скорости фильтрации.
Средняя действительная скорость движения жидкости W равна отношению объемного расхода (дебита) к площади просветов Fп:
.
Скорость фильтрации и средняя действительная скорость движения связаны соотношением:
,
где m’ - коэффициент просветности, m’ = m.
Истинное значение действительной скорости течения определится из соотношения:
.
Пользоваться понятием «средняя скорость фильтрации» достаточно удобно, поскольку с ее помощью пласт можно рассматривать как непрерывное поле скоростей и давлений, величина которых в каждой точке пласта является только функцией координат этой точки и времени и не зависит от свойств среды.
Обобщенный теоретический закон фильтрации
Форма и размер сечений поровых каналов резко и хаотически меняются в пространстве. Это затрудняет точное решение уравнений течения вязкой жидкости. Поэтому первые теоретические исследования порового пространства проводились с помощью идеализированных моделей. Такими моделями являлись идеальный и фиктивный грунты.
Под идеальным грунтом понимается модель пористой среды, поровые каналы которой представляют собой пучок тонких цилиндрических трубок (капилляров) с параллельными осями.
Фиктивным грунтом называется модель пористой среды, состоящая из шарообразных частиц одинакового диаметра и служащая прообразом реального грунта.
Модель идеального грунта использовалась как ступень для перехода от закономерностей трубной гидравлики к движению жидкости в фиктивном, а затем реальном грунтах.
Известно, что гидравлические потери напора при движении вязкой жидкости по трубам определяются формулой Пуазейля:
, (1.1)
где Dh - потеря напора на трение на участке длиной DL; m - динамическая вязкость жидкости; r - плотность жидкости; D - диаметр трубы.
Обозначим площадь поперечного сечения трубы f:
.
Запишем уравнение (1.1) в виде:
.
Поскольку rgDh = DP, где DP - перепад давления на длине DL, имеем:
.
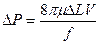Отсюда выразим скорость:
- справедливо для трубы или идеального грунта. (1.2)
Чтобы перейти от идеального грунта к фиктивному, очевидно, следует связать площадь сечения единичного порового канала f с площадью просветности фиктивного грунта, а также учесть форму порового пространства. Это можно сделать, геометризируя сечения поровых каналов и выражая плотность укладки шарообразных частиц (угол 60о£q£90о) через пористость. В результате разными исследователями были получены однотипные формулы закона фильтрации жидкости в фиктивном грунте:
, (1.3)
где F - площадь сечения пористой среды, d - диаметр частиц.
В них по-разному определялся лишь параметр s:
; 
; 
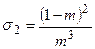и т.д.
По предложению Л.С.Лейбензона безразмерный параметр 1/96s, зависящий от пористости, был назван числом Слихтера. Из формулы (1.3) имеем:
. (1.4)
При фильтрации жидкости в реальном грунте число Sl является функцией не только пористости, но и зависит от структуры порового пространства. Кроме того, для корректного перехода от фиктивного грунта к реальному необходимо, чтобы эти грунты были эквивалентны (т.е. должны быть равны гидравлические сопротивления, оказываемые потоку жидкости). С этой целью вместо диаметра d частиц фиктивного грунта вводится эффективный диаметр dэ, определяемый по результатам механического анализа естественного грунта.
С учетом сказанного, а также имея в виду, что Q/F=V, получаем обобщенное выражение теоретических законов фильтрации:
. (1.5)
Здесь e - некоторый параметр, характеризующий структуру порового пространства.
Значения числа Sl у различных авторов различны, поскольку каждый из них при выводе закона фильтрации по-своему подходил к решению задачи о сведении фиктивного грунта к идеальному. Однако общим для всех уравнений является линейная зависимость между скоростью фильтрации и перепадом давления на единице длины, а также присутствие в формуле, выражающей закон фильтрации, квадрата эффективного диаметра частиц и числа Слихтера, зависящего от коэффициента пористости и структуры порового пространства.
В дифференциальной (векторной) форме уравнение (1.5) запишется в виде:
. (1.6)
Знак минус показывает, что давление уменьшается в положительном направлении оси l в сторону движения потока (dl прирастает, а dp уменьшается). Ввод знака «минус» в правую часть уравнения позволяет получить в левой его части абсолютное значение скорости.
