Если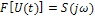 
и A постоянная величина, то
Теорема смещения (запаздывания )
Если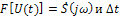 
- отрезок времени, то
Следовательно, спектральная плотность импульса, возникшего на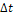 
секунд позднее, равна спектральной плотности исходного импульса 
, умноженной на 
. Этот множитель изменяет только фазовые соотношения в спектре.
Существенное влияние на состав спектральной плотности оказывает симметрия импульса. Если четная функция (симметрия относительно оси ординат), т. е. 
, то спектральная плотность 
является чисто действительной функцией частоты. В случае, когда 
нечетная функция (симметрия относительно начала координат), т. е.
чисто мнимая функция.
Пример 2. Найти спектральную плотность экспоненциального импульса
где Е - амплитуда импульса;
параметр;
- момент "начала" импульса;
- вспомогательная единичная функция, обеспечивающая 
при всех 
, так как
Считают, что экспоненциальный импульс, представленный на рис.3.а в нормированном виде 
при 
, существует в пределах интервала 
, так как при 
"хвост" импульса меньше уровня 1%.
После подстановки 
в формулу (23), получаем при
Так как 
,то спектральную плотность можно представить, в показательной форме:
Модуль 
и аргумент 
спектральной плотности импульса, т. е. амплитудная и фазовая спектральные характеристики, изображены сплошной и пунктирной кривыми на рис.3,б.
Последнее выражение можно использовать два нахождении по формуле (22) спектра периодической последовательности экспоненциальных импульсов, изображенной на рис.3.г для случая 
Амплитудно-частотный спектр последовательности приведен на рис.3.в, Этот спектр – дискретный, частоты соседних составлявших различаются на 
, а функция 
играет роль огибающей амплитуд спектра. Нетрудно проследить, как при увеличат периода 
(уменьшении ) составляющие спектра сближаются по частоте и уменьшается по амплитуде. В пределе (при 
и 
) получится; сплошной спектр одиночного импульса с бесконечно малыми по амплитуде составляющими.
В заключение определим ширину спектра экспоненциального импульса, используя формулу (26). Полная энергия импульса равна:
Вычисление левой части формулы (26) не вызывает трудностей, так как, обозначив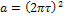 
получаем табличный интеграл
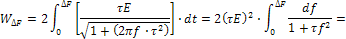
После подстановки полученных выражений 
и 
в формулу (26) находим ширину спектра импульса 
.
Рис.З.Экспоненциальный импульс, его спектральная функции и амплитудный спектр периодической последовательности импульсов.
|
Рис.4
Таким образом чем короче импульс, тем шире его спектр.
