Введение в анализ. Дифференциальное исчисление
Методические указания и задания
Для выполнения типового расчета
по курсу «МАТЕМАТИКА»
Направление подготовки
Биотехнология
Профиль подготовки
Биотехнология
Саратов 2014
Введение в анализ. Дифференциальное исчисление: метод. указания и задания для выполнениятипового расчета по курсу «Математика» для направления подготовки 240700.62 Биотехнология / сост. Т.В. Кириллова //ФГБОУ ВПО «Саратовский ГАУ».- Саратов, 2013.-
Методические указания и задания для выполнения типового расчета по дисциплине «Математика» составлены в соответствии с программой и предназначены для студентов направления подготовки 240700.62 Биотехнология. Они содержат рекомендации, примеры и задания к выполнению типового расчета. Позволяют студентам освоить основные методы дифференциального исчисления необходимые для анализа процессов и явлений в ходе поиска оптимальных решений практических задач.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Работа выполняется на листах формата А4 (210х297), которые затем скрепляются.
Решение заданий следует сопровождать краткими пояснениями.
Исходные данные для заданий типового расчета представлены в таблицах. Из таблицы каждый студент выбирает строки с номерами вариант, которые соответствуют номеру в списке группового журнала.
Общие методические рекомендации по выполнению расчетно-графических работ
К выполнению каждой расчетно-графической работы следует приступать только после изучения соответствующего материала курса математики по учебникам и решения задач, указанных в каждой теме. При этом следует руководствоваться следующими указаниями:
1. Каждую работу следует выполнять в тетради. Решения всех задач и пояснения к ним должны быть достаточно подробными. При необходимости следует делать соответствующие ссылки на вопросы теории с указанием формул, теорем, выводов, которые используются при решении данной задачи. Все вычисления (в том числе и вспомогательные) необходимо делать полностью. Чертежи и графики должны быть выполнены (желательно на миллиметровой бумаге) аккуратно и четко с указанием единиц масштаба, координатных осей и других элементов чертежа. Объяснения к задачам должны соответствовать тем обозначениям, которые даны на чертеже.
2. Для замечаний преподавателя необходимо на каждой странице оставлять поля шириной 3 - 4 см. После получения проверенной расчетно-графической работы (как зачтенной, так и незачтенной) студент должен исправить в ней все отмеченные рецензентом недостатки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и предоставить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
3.Расчетно-графические работы должны выполняться самостоятельно. Если будет установлено, что та или иная работа выполнена несамостоятельно, то она не будет зачтена, даже если в этой работе все задачи решены верно.
5. В период экзаменационной сессии студент обязан представить все зачтенные расчетно-графические работы.
Консультации
Если в процессе изучения материала или при решении той или иной задачи у студента возникают вопросы, на которые он не может ответить сам, то можно обратиться к преподавателю для получения письменной или устной консультации. В случае письменной консультации в запросе следует, возможно, более точно указать характер затруднения. При этом обязательно следует указать полное название книги, год издания и страницу, где трактуется непонятный для студента вопрос или помещена соответствующая задача.
Типовой пример 1.
Вычислить предел  ;
;
Решение типового примера.
Подстановка предельного значения переменной x в выражение, стоящее под знаком предела приводит к неопределенности  .
.
Для устранения этой неопределенности числитель и знаменатель дроби разложим на множители и сократим дробь на общий множитель.

Типовой пример 2.
Вычислить предел 
Решение типового примера.
Числитель и знаменатель дроби стремятся к бесконечности (неопределенность вида  ).
).
Для устранения этой неопределенности числитель и знаменатель дроби делим почленно на старшую степень переменной x в данной дроби, т.е. на x3.
 .
. 
Типовой пример 3.
Вычислить предел 

Решение типового примера.
Подстановка предельного значения переменной x в выражение, стоящее под знаком предела, приводит к неопределенности  .Для устранения неопределенности в числитле дроби следует избавиться от рациональности умножением числителя и знаменателя на сопряженное выражение
.Для устранения неопределенности в числитле дроби следует избавиться от рациональности умножением числителя и знаменателя на сопряженное выражение  , а знаменатель разложить на множители.
, а знаменатель разложить на множители.


Типовой пример 4.
Вычислить предел  .
.
Решение типового примера.
Вычисление предела начинаем с подстановки в выражение, стоящее под знаком предела, предельного значения x, т.е. вычисляем пределы.

Таким образом, в результате подстановки  в функцию, получим
в функцию, получим
 т.к. число a < 1 при возведении в степень, стремящуюся к бесконечности, стремится к нулю.
т.к. число a < 1 при возведении в степень, стремящуюся к бесконечности, стремится к нулю.
Типовой пример 5.
Вычислить предел 
Решение типового примера.
Применяя правило Лопиталя, имеем




Типовой пример 6
Найти производную Функции
y= 

Решение типового примера.
Воспользуемся известным правилом дифференцирования суммы и разности функций  и теоремой о производной сложной функции
и теоремой о производной сложной функции 


Типовой пример 7.
Найти производную функции

Решение типового примера.
Воспользуемся правилом дифференцирования произведения двух функций
 и формулами
и формулами


Типовой пример 8.
Найти производную функции 
Решение типового примера.
Воспользуемся следующими формулами дифференцирования:


Типовой пример 9.
Провести полное исследование функции  и построить ее график
и построить ее график
Решение типового примера.
Область определения функции  т.е. вся числовая прямая, кроме точки x = 0, где знаменатель обращается в нуль
т.е. вся числовая прямая, кроме точки x = 0, где знаменатель обращается в нуль
2.Функция не является ни четной, ни нечетной, т.к. не выполняется ни одно из условий

В самом деле  полученное выражение не равно ни
полученное выражение не равно ни  ,ни
,ни 
Т. о. график функции не является симметричной кривой.
Функция не является периодической
3. Функция непрерывна всюду, кроме точки  (как элементарная
(как элементарная  функция)
функция)  , т.е. прямая
, т.е. прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
4.Точек пересечения с осью ординат график функции не имеет, т. к.  . Для определения точек пересечения с осью абсцисс решим уравнение
. Для определения точек пересечения с осью абсцисс решим уравнение
 ; т.к.
; т.к.  то
то  , т.е. график функции пересекает ось абсцисс в точке
, т.е. график функции пересекает ось абсцисс в точке  .
.
5.Для определения точек экстремума, интервалов монотонности функции найдем первую производную

Приравняем производную к нулю и найдем критические точки 
При  производная не существует,но эта точка не является критической, т.к. в ней не существует и сама функция.
производная не существует,но эта точка не является критической, т.к. в ней не существует и сама функция.
Критическая точка разбивает всю область определения функции на следующие интервалы  .
.
Заполним следующую таблицу

| 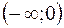
| 
| 
| 
| 
|

| - | не сущ. | - | + | |
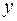
| не сущ. | min |
Найдем 
Функция имеет минимум в точке 
6  .Для определения интервалов выпуклости, вогнутости, точек перегиба найдем вторую производную
.Для определения интервалов выпуклости, вогнутости, точек перегиба найдем вторую производную
 ;
;
Вторая производная  в области определения функции положительна, поэтому график всюду вогнут, точек перегиба нет.
в области определения функции положительна, поэтому график всюду вогнут, точек перегиба нет.
7 Найдем наклонные асимптоты кривой, которые имеют уравнение 
Т.о. наклонная асимптота кривой имеет уравнение  .
.
8.Строим график функции. Сначала на координатной плоскости строим асимптоты  и
и  ;затем характерные точки.
;затем характерные точки.
 | |||
 | |||


|
(2,3)


|

Типовой пример10.
Найти наименьшее и наибольшее значение функции  на отрезке [0;3]
на отрезке [0;3]
Решение типового примера.
Функция может достигать своего наименьшего и наибольшего значений либо в критических точках, либо на концах заданного отрезка.
Вычислив значения функции в этих точках, простым сравнением полученных значений выбираем наибольшее и наименьшее.
Найдем критические точки:

т.к.знаменатель  ,то числитель должен быть
,то числитель должен быть
равен нулю. т.е. 

Отрезку [0;3] принадлежит критическая точка 
Вычислим значения функции в точках


Отсюда следует

Типовой пример 11.
Вычислить приближенно с помощью дифференциала  ;
;
Решение типового примера.
Если 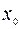 получает некоторое приращение
получает некоторое приращение  , то соответствующее приращение функции
, то соответствующее приращение функции  можно представить в виде
можно представить в виде  где
где  есть бесконечно малая величина высшего порядка относительно
есть бесконечно малая величина высшего порядка относительно 
В приближенных вычислениях принимают  или
или  , откуда
, откуда 
Обозначая  через
через  , получаем формулу приближенного вычисления
, получаем формулу приближенного вычисления 
Следует учесть, что значение  нужно представить в виде
нужно представить в виде  . таким образом, чтобы значение
. таким образом, чтобы значение  было известно или легко вычислялось, а величина приращения
было известно или легко вычислялось, а величина приращения  была по возможности наименьшей.
была по возможности наименьшей.
Итак  и требуется найти
и требуется найти  . Число 1000 можно представить в виде
. Число 1000 можно представить в виде  так, чтобы
так, чтобы 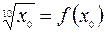 , а также
, а также  легко вычислялось, и кроме того,
легко вычислялось, и кроме того,  было по возможности минимальным. Так как
было по возможности минимальным. Так как  и
и  , то целесообразно взять
, то целесообразно взять  . Тогда
. Тогда  , откуда
, откуда  . В сравнении с заданным числом
. В сравнении с заданным числом 
 величина
величина 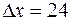 является небольшой, поэтому можно воспользоваться формулой (1).Для этого вычислим
является небольшой, поэтому можно воспользоваться формулой (1).Для этого вычислим  .
.

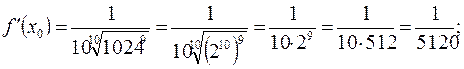
Тогда  .
.
Расчетные задания.
Задание1
Вычислить предел:







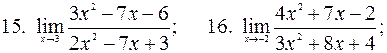

17.  ; 18.
; 18.  ;
; 
19.  ; 20.
; 20. 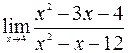 ;
;
21.  ; 22.
; 22.  ;
;
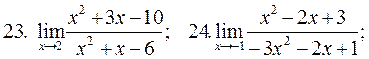
25.  ; 26.
; 26.  ;
;


Задание 2
Вычислить предел:
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14.  ;
; 
15. 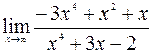 ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20. 

21.  22.
22.  ;
;
23.  ; 24.
; 24.  ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28.  ;
;
29.  ; 30.
; 30.  ;
;
Задание 3.
Вычислить пределы:
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4. 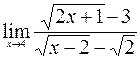 ;
;
5.  ; 6.
; 6.  ;
;
7. 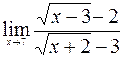 ; 8.
; 8. 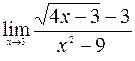 ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13. 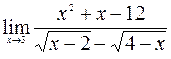 ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ;
;
23.  ; 24.
; 24.  ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28.  ;
;
29.  ; 30.
; 30.  ;
;
Задание 4.
Вычислить предел:
1.  ; 2.
; 2.  ;
;
2.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12
; 12  ;
;
13.  ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20. 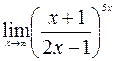 ;
;
21.  ; 22.
; 22.  ;
;
23.  ; 24.
; 24.  ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28.  ;
;
29.  ; 30.
; 30.  ;
;
Задание 5
Вычислить придел
1.  2
2 
3  4
4  ;
;
5  6
6 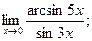
7  8
8 
9  10
10 
11  12
12  ;
;
13  14
14 
15 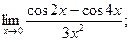 16
16 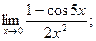
17  18
18 
19  20
20 
21  22
22 
23  24
24 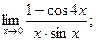
25  26
26 
27  28
28 
29  30
30 
Задание 6.
Найти производную функций:
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  10.
10.  ;
;
11.  ; 12.
; 12.  ;
;
13.  .
.  14.
14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20.  ;
;
21. 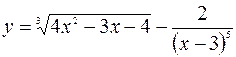 ; 22.
; 22.  ;
;
23.  ; 24.
; 24.  ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28.  ;
;
29.  ; 30.
; 30.  ;
;
Задание 7.
Найти производную функции:
1.  ; 2.
; 2.  ;
;
3.  ; 3.
; 3.  ;
;
5. 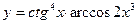 ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10. 
 ;
;
11.  ; 12.
; 12.  ;
;
13. 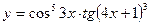 ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18. 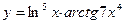 ;
;
19.  ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ;
;
23.  ; 24.
; 24. 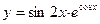 ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28.  ;
;
29.  ; 30.
; 30.  ;
;
Задание 8.
Найти производную функции:
1. 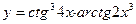 ; 2.
; 2.  ;
;
4.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18. 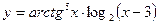 ;
;
19. 
 ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ;
;
23.  ; 24.
; 24. 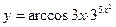 ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28. 
29.  ; 30.
; 30.  ;
;
Задание 9.
Провести полное исследование функции и построить ее график.
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11. 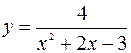 ; 12.;
; 12.; 
13.  ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19. 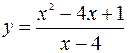 ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ;
;
23.  ; 24.
; 24.  ;
;
25.  ; 26.
; 26.  ;
;
27.  ; 28.
; 28.  ;
;
29.  ; 30.
; 30.  ;
;
Задание 10.
Найти наибольшее и наименьшее значение функции на отрезке [a;b]:
1.  ; [-2;0]; 2.
; [-2;0]; 2.  ; [-2;1];
; [-2;1];
3.  ; [0;3]; 4.
; [0;3]; 4.  ; [2;2];
; [2;2];
5.  ;
; 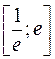 ; 6.
; 6. 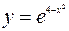 ; [1;3];
; [1;3];
7.  ; [-3;-1]; 8.
; [-3;-1]; 8.  ; [-1;2];
; [-1;2];
9. 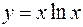 ;
;  ; 10.
; 10. 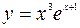 ; [-4;0];
; [-4;0];
11.  ; [0;3]; 12.
; [0;3]; 12.  ; [
; [  ;0];
;0];
13.  ; [0;5]; 14.
; [0;5]; 14.  ; [-2;2];
; [-2;2];
15.  ; [-1;
; [-1;  ]; 16.
]; 16.  ; [-1;1];
; [-1;1];
17.  ; [1;2] 18.
; [1;2] 18.  ; [-2;2];
; [-2;2];
19.  ; [0;1]; 20.
; [0;1]; 20.  ; [1;2];
; [1;2];
21.  ; [-4;2] 22.
; [-4;2] 22.  ; [-4;-1];
; [-4;-1];
23.  ; [-2;1]; 24.
; [-2;1]; 24.  ; [-5;1];
; [-5;1];
25.  ; [1;5]; 26.
; [1;5]; 26.  ; [-2;1];
; [-2;1];
27. 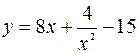 ; [
; [  ;2]; 28.
;2]; 28.  ; [-1;2];
; [-1;2];
29.  ; [-2;-
; [-2;-  ]; 30.
]; 30.  ; [0;3];
; [0;3];
Задание 11.
Вычислить приближенно с помощью дифференциала:
1.  ; x=0,998; 2.
; x=0,998; 2.  ; x=1,03;
; x=1,03;
3.  ; x=2,01; 4.
; x=2,01; 4.  ; x=8,24;
; x=8,24;
5. 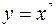 ; x=1,996; 6.
; x=1,996; 6.  ; x=7,64;
; x=7,64;
7.  ; x=2,56; 8.
; x=2,56; 8.  ; x=1,016;
; x=1,016;
9.  ; x=8,36; 10.
; x=8,36; 10.  ; x=4,16;
; x=4,16;
11 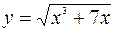 ; x=1,012; 12.
; x=1,012; 12.  ; x=7,76;
; x=7,76;
13.  ; x=0,98; 14.
; x=0,98; 14.  ; x=0,08;
; x=0,08;
15.  ; x=0,97; 16.
; x=0,97; 16.  ; x=1,97;
; x=1,97;
17.  ; x=1,021; 18.
; x=1,021; 18.  ; x=26,46;
; x=26,46;
19.  ; x=1,012; 20.
; x=1,012; 20.  ; x=1,21;
; x=1,21;
21.  ; x=27,54; 22.
; x=27,54; 22.  ; x=2,01;
; x=2,01;
23. 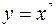 ; x=2,002; 24.
; x=2,002; 24. 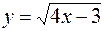 ; x=1,78;
; x=1,78;
25.  ; x=3,998; 26.
; x=3,998; 26.  ; x=2,997;
; x=2,997;
27.  ; x=0,98; 28.
; x=0,98; 28.  ; x=0,01;
; x=0,01;
29.  ; x=0,01; 30.
; x=0,01; 30.  ; x=1,02.
; x=1,02.
КРИТЕРИЙ ОЦЕНКИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
Качество выполнения внеаудиторной самостоятельной работы студентов оценивается посредством текущего контроля самостоятельной работы студентов. Текущий контроль СРС – это форма планомерного контроля качества и объема приобретаемых студентом компетенций в процессе изучения дисциплины, проводится на практических и семинарских занятиях и во время консультаций преподавателя.
Максимальное количество баллов «отлично»студент получает, если:
- обстоятельно с достаточной полнотой излагает соответствующую тему;
- раскрыл содержание практической части задания на 85%-100%;
- дает правильные формулировки, точные определения, понятия терминов;
- правильно отвечает на дополнительные вопросы преподавателя, имеющие целью выяснить степень понимания студентом данного материала.
Оценку «хорошо» студент получает, если:
- неполно, но правильно решено задание;
- если студент раскрыл содержание практической части задания на 70%-84%;
- при решении были допущены 1-2 несущественные ошибки, которые он исправляет после замечания преподавателя;
- дает правильные формулировки, точные определения, понятия терминов;
- правильно отвечает на дополнительные вопросы преподавателя, имеющие целью выяснить степень понимания студентом данного материала.
Оценку «удовлетворительно» студент получает, если:
- неполно, но правильно изложено задание;
- если студент раскрыл содержание практической части задания на 50%-69%;
- при решении было допущено 2 существенные ошибки;
- излагает выполнение задания недостаточно логично и последовательно;
- затрудняется при ответах на вопросы преподавателя.
Оценка «неудовлетворительно» студент получает, если:
- неполно изложено задание;
- если студент раскрыл содержание практической части задания менее, чем на 49%;
- при изложении были допущены существенные ошибки, т.е. если оно не удовлетворяет требованиям, установленным преподавателем к данному виду работы.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
а) основная литература (библиотека СГАУ
1. Черненко, В. Д. Высшая математика в примерах и задачах. В 3-х т.: учебное пособие. Т. 2 / В. Д. Черненко. - СПб.: Политехника, 2003. - 477 с. - (Учебное пособие для вузов). - ISBN 5-7325-0768-X
2. Виленкин, И. В. Высшая математика для студентов экономических, технических, естественно-научных специальностей вузов: Ростов: учеб. пособие / И. В. Виленкин. - 3-е изд., испр.. - Ростов н/Д.: Феникс, 2005. - 414 с.: ил. - (Высшее образование). - ISBN 5-222-07171-5
3. Шипачев, В. С. Курс высшей математики: учебник для вузов / Под ред. А. Н. Тихонова. - 3-е изд., испр. - М.: ОНИКС, 2007. - 600 с.
4. Линьков, В. М. Высшая математика в примерах и задачах. Компьютерный практикум: учебное пособие / В. М. Линьков, Н. Н. Яремко. - М.: Финансы и статистика, 2006. - 320 с. - ISBN 5-279-027731
5. Шипачев, В. С. Высшая математика: учебник / В. С. Шипачев. - 8-е изд., стер. - М.: Высш. шк., 2007. - 479 с. - ISBN 5-06-003959-5
6. Вентцель, Е. С. Теория вероятностей и ее инженерные приложения: учебное пособие / Е. С. Вентцель, Л. А. Овчаров. - 4-е изд., стер. - М.: Высш. шк., 2007. - 491 с. - (Учебники для вузов. Математика). - ISBN 978-5-06-005714-0
7. Бугров, Я. С. Высшая математика. В 3-х т.: учебник. Т. 3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я. С. Бугров, С. М. Никольский. - 7-е изд., стер. - М.: Дрофа, 2005. - 511 с. - (Высшее образование) (Современный учебник). - ISBN 5-7107-9898-3
8. Самарин, Ю. П.. Высшая математика: учебное пособие / Ю. П. Самарин, Г. А. Сахабиева, В. А. Сабахиев. - М.: Машиностроение, 2006. - 432 с. - (В для вузов). - ISBN 5-217-03354-1.
9. Тыртышников, Е. Е. Матричный анализ и линейная алгебра: учебное пособие / Е. Е. Тыртышников. - М.: Физматлит, 2007. - 480 с. - ISBN 978-5-9221-0778-5
10. Шириков, В. Ф.. Теория вероятностей: учебное пособие / В. Ф. Шириков, С. М. Зарбалиев. - М.: КолосС, 2008. - 389 с. - (Учебники и учеб. пособия для студентов высш. учеб. заведений). - ISBN 978-5-9532-0621-1
11. Демидович, Б. П.. Задачи и упражнения по математическому анализу для втузов: учебное пособие / ред. Б. П. Демидович. - М.: Астрель; М.: АСТ, 2004. - 495 с.: ил. - ISBN 5-271-01118-6. - ISBN 5-17-002965-9
12. Демидович, Б. П. Краткий курс высшей математики: учебное пособие / Б. П. Демидович, В. А. Кудрявцев. - М.: Астрель; М.: АСТ, 2007. - 654 с. -ISBN 5-271-01318-9. - ISBN 5-17-004601-4
13. Омельченко, В. П. Математика: учебное пособие / В. П. Омельченко, Э. В. Курбатова. - Ростов н/Д.: Феникс, 2005. - 380 с. - (Среднее проф. образование). - ISBN 5-222-06004-7
14. Данко, П. Е. Высшая математика в упражнениях и задачах: в 2 ч. Ч. 1 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - М.: Оникс 21 век; М.: Мир и образование, 2003. - 304 c.: ил. - ISBN 5-329-00326-1. - ISBN 5-94666-008-X
15. Дадаян, А. А. Математика [Текст]: учебник / А. А. Дадаян; ред. В. В. Сенатов. - М.: Форум, Инфра-М, 2005. - 552 с. - (Профессиональное образование). - ISBN 5-8199-0036-7: 168 р. - ISBN 5-16-000985-х
16. Зайцев, И. А. Высшая математика: учебник / И. А. Зайцев. - 4-е изд., стереотип. - М.: Дрофа, 2005. - 398 с.: ил. - ISBN 5-7107-9071-0
17. Богомолов, Н. В. Практические занятия по математике: учебное пособие / Н. В. Богомолов. - 8-е изд., стер. - М.: Высш. шк., 2006. - 495 с. - ISBN5-06-003940-4
18. Виленкин, И. В. Высшая математика: линейная алгебра, аналитическая геометрия, дифференциальное и интегральное исчисление [Текст]: учебное пособие / И. В. Виленкин, В. М. Гробер. - 6-е изд. - Ростов н/Д.: Феникс, 2011. - 414 с.: ил. - (Высшее образование). -ISBN978-5-222-18236-9
19. Юрьева, А. А. Руководство к решению задач по теории вероятностей и математической статистике.: учебное пособие / А. А. Юрьева. - 2-е изд., испр. - Саратов: ФГОУ ВПО "Саратовский ГАУ", 2009. - 208 с.
20. Прохоров, Ю.В. Вероятность и математическая статистика: энциклопедический словарь / ред. Ю. В. Прохоров. - Репр. воспроизведение изд. - М.: Большая Российская Энциклопедия, 2003. - 910 с. - (Золотой фонд). - ISBN 5-7107-7433-2
21. Ермакова, В.И. Теория вероятностей и математическая статистика: учебное пособие / ред. В. И. Ермакова. - М.: Инфра-М, 2004. - 287 с. - (Высшее образование). - ISBN 5-16 001561-2
22. Гмурман, В. Е. Теория вероятностей и математическая статистика: учебное пособие / В. Е. Гмурман. - 12-е изд., перераб. - М.: Высш. образование, 2006. - 479 с.: ил. - (Основы наук).
23. Кириллова, Т. В., Хучраева Т.С. Элементы математической статистики / Т. В., Хучраева Т.С. Кириллова. - Саратов: Сарат. гос. агр. ун-т, 2004. - 60 с. - ISBN 5-7011-0394-3
24. Шириков, Виктор Филиппович. Математическая статистика: учебное пособие / В. Ф. Шириков, С. М. Зарбалиев. - М.: КолосС, 2009. - 480 с.: ил. - (Учебники и учеб. пособия для студентов высш. учеб. заведений). - ISBN 978-5-9532-0657-0
25. Белов, А. А. Теория вероятностей и математическая статистика: учебник / А. А. Белов, Б. А. Баллод, Н. Н. Елизарова. - Ростов н/Д.: Феник






