6. Анализ полученных данных и вывод. Полученные в результате
работы программы данные должны подтвердить или опровергнуть
правильность теоретических выводов об условиях перехода в
«комбинированном» методе поиска.
Результатом является: графики, схемы, характеризующие условия
перехода в «комбинированном» методе поиска, позволяющие оценить
эффективность использования того или иного условия перехода.
Описание задачи. Особенности классических алгоритмов преследования цели и смысл решения задачи преследования.
Классические методы преследования: погони, постоянного угла упреждения, параллельного и пропорционального сближения.
Введем следующие обозначения:
Vп – вектор скорости преследователя (П);
Vц – вектор скорости цели (Ц);
r = r(t) – текущее расстояние между П и Ц;
γ – курсовой угол преследователя, т.е. угол между вектором скорости Vп и линией визирования (линией преследователь - цель);
φ – курсовой угол цели (угол между вектором скорости Vц и линией визирования);
η – угол визирования (угол между фиксированным направлением ПN и линией визирования);
ψ – курс преследования (угол между ПN и вектором Vп).
Метод погони (чистым преследованием, преследованием по кривой погони «собачьей кривой») называют метод преследования, при котором вектор скорости преследования в любой момент времени направлен на цель, т.е. его программный курсовой угол γ0 (γ обозначает фактический круговой угол преследования) равен нулю:
γ0(t) = 0, t0 ≤ t ≤ tf,(1)
где t0, tf - начальный и конечный моменты времени преследования.
Рис 1.
Пусть цель движется прямолинейно с постоянной скоростью Vц и скоростью преследователя Vп также постоянна. Тогда кинематические уравнения (т.е. уравнения без учета динамики преследователя и цели) преследования по кривой погони имеют следующий вид:
r = Vц cos φ - Vп, (2)
φr = - Vц sin φ. (3)
Разделив первое уравнение на второе и проинтегрировав, получим
(4)
(5)
в силу симметрии достаточно ограничиться значениями φ0 ϵ [0, π]. Из (3) и (4) следует, что φ со временем убывает и r → 0 при φ → 0.
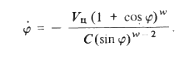Подставив выражение для r из (4) в (3), получим
(6)
Из этого равенства вытекает:
Хотя при w ≤ 2 угловая скорость ЛВ остается конечной при всех t ϵ [t0, tf], её максимальное значение (по модулю) может быть большим.
(7)
При w ≥ 2 максимум | φ | в конечный момент преследования, а при w < 2 – в тот момент, когда cos φ = w/2.
Итак, при методе погони, каковы бы ни были начальные условия преследования, преследователь приближается к цели сзади, и кривая погони (программная траектория, соответствующая методу погони) всегда, за исключением случаев, когда преследователь начинает преследование с острых догонных курсов, сильно искривлена. Поэтому возможны значительные промахи даже в том случае, когда цель не совершает маневра, так как преследователь со временем сходит с кривой погони. В связи с этим метод погони целесообразно использовать при преследовании тихоходных, неманеврирующих целей с острых догонных курсов, а также тогда, когда к точности наведения не предъявляются жесткие требования.
Достоинствами метода погони является его помехоустойчивость и то обстоятельство, что для его реализации достаточно иметь информацию типа «да-нет»: находится ли цель слева или справа от вектора скорости преследователя. Приборно проще определять положение цели относительно продольной оси. Поэтому часто под методом погони также понимают метод преследования, при котором при движении преследователя по программной траектории его продольная ось направлена на цель. Такой метод иногда называют прямым методом наведения.
Метод постоянного угла упреждения (преследование с упреждением) –метод наведения, при котором программный курсовой угол преследователя равен некоторой фиксированной величине γ0:
γ0(t) = γ0, t0 ≤ t ≤ tf,(8)
Значение γ0 должно быть таким, чтобы выполнялось неравенство
(Vп / Vц) |sin γ0| ≤ 1, (9)
Так как иначе программная траектория является спиралью, описывающей относительно цели бесконечное число витков, и преследователь вообще не попадает в цель.
Преследование с упреждением описывается уравнениями (см. рис 1)
(10)
(11)
Разделив одно уравнение на другое и проинтегрировав, получим
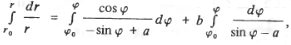(12)
где
(13)
При условии
(14)
,
последний интеграл в (12)
Поэтому для r из (12) имеем
(15)
При условии
a = w sin γ0 = 1 (16)
интеграл
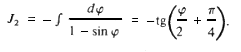
В этом случае
(17)
Подставив выражение для r из (15) в (11), для угловой скорости w = φ получим
(18)
(19)
Эта запись имеет смысл, если a > sin φ0 и a > sin φ. (20)
Если a < sin φ0 и a < sin φ, (21)
то из (11) и (15) следует
(22)
(23)
Из (15) следует, что r → 0 при sin φ → a, или при
φ → φи = arcsin a = arcsin (w sin γ0). (24)
Уравнение sin φ = a в интервале [0, π] имеет два решения: φ1 = φи и φ2 = π - φи. Но второе решение неустойчиво. Действительно, в силу симметрии достаточно ограничиться значениями φ0 ϵ [0, π] и γ0 ϵ [0, av]. Ограничение на γ0 сверху определено условием (9). Как следует из (11), при 0 < φ0 < φи угловая скорость φ > 0 и φ → φи, при φи < φ0 < φ2 угловая скорость φ < 0 и опять φ → φи, при φ2 < φ0 ≤ π угловая скорость φ > 0 и φ → 2 π + φи, т.е. опять с точностью до периода предельное значение φ равно φи. Если φ0 = φ2, то небольшое возмущение приводит к тому, что φ → φи.
Рассматривая (18) и (19) при φ → φи, заключаем, что
Из приведенного анализа можно получить следующие рекомендации. Кроме обеспечения условия (9) при преследовании цели на встречных курсах (π/2 < φ0 < π) постоянный угол упреждения γ0 нужно выбрать так, чтобы выполнялось условие a < sin φ0 или γ0 ≤ arcsin (v sin φ0), v = Vц/Vп.
Иначе преследователь опишет большую дугу: пересечет траекторию цель сначала спереди, затем сзади и только после этого он сможет настигнуть цель.
Метод постоянного угла упреждения является обобщением метода погони и имеет перед ним то преимущество, что при соответствующем выборе угла упреждения γ0 программная траектория преследования с упреждением менее искривлена, чем кривая погони. Кроме того, кривая погони подходит к цели сзади при φ = 0, тогда как кривая преследования с упреждением присущи такие же недостатки, что и методу погони. Метод постоянного угла упреждения обладает почти такой же помехоустойчивостью, что и метод погони, но для его реализации необходима информация о пеленге цели или информация типа «да-нет» относительно прямой, образующей с вектором скорости или продольной осью преследователя угол γ0. Кроме того, при использовании метода постоянного угла упреждения необходимо еще знать направление движения цели для правильного определения знака угла упреждения.
