Объектом исследования являются две нелинейные цепи постоянного тока, схемы которых приведены в протоколе испытаний на рис.6 – 7. Первая цепь (рис.6.) состоит из двух параллельно включенных ламп накаливания, которые рассматриваются как одна лампа. Вторая цепь (рис.7) состоит из стабилитрона и резистора, включенных последовательно. Все элементы цепей смонтированы на плате №5 лабораторного стенда.
Питание цепей осуществляется от источника постоянного тока с регулируемым напряжением. В качестве измерительных приборов используются многопредельный миллиамперметр Э-377 и цифровой или стрелочный электронный вольтметр.
Порядок проведения эксперимента
1. Снятие АВХ ламп накаливания. Собрать электрическую цепь согласно схеме, представленной на рис.6 протокола испытаний. После проверки цепи преподавателем подать на нее напряжение. Для этого выключатели В1(3~36 В), В2(-20 В) и ВЗ-1(плата №3) установить в положение "Вкл.", а выключатель ВЗ-2 (плата №3) установить в положение П. Изменяя напряжение источника питания от нуля до максимума, снять пять отсчетов напряжения U и тока Iлн прямой ветви АВХ. Показания приборов записать в табл.1 протокола испытаний. Изменив полярность напряжения на зажимах ламп накаливания, таким же образом снять и записать в табл.1 значения напряжения и тока обратной ветви АВХ.
2. Снятие АВХ стабилитрона и резистора. Собрать электрическую цепь согласно схеме, представленной на рис 7 протокола испытаний. После проверки цепи преподавателем подать на нее напряжение и снять АВХ стабилитрона, резистора и всей цепи. Для этого, изменяя напряжение источника от нуля до максимума, снимать показания и записывать в табл.2 протокола испытаний значения тока I, общего напряжения U и напряжений настабилитроне Uст и резисторе UR.
3. Полученные результаты согласовать с преподавателем, после чего разобрать электрическую цепь.
Обработка результатов эксперимента
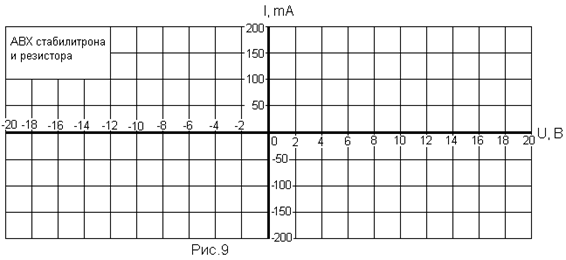
1. На рис. 8 (прил.) по данным табл.2 построить в одних осях координат АВХ стабилитрона I(|Uст), резистора I (UR) и всей цепи I(U). Построить АВХ всей цепи, просуммировав характеристики стабилитрона и резистора по оси U, и сравнить ее с экспериментальной.
2. По заданному преподавателем значению напряжения U определить ток и падения напряжений на элементах цепи (рис.7).
3. Используя построенную АВХ резистора, определить его сопротивление R.
4. По данным табл.1 построить на рис.9 (прил.) АВХ ламп накаливания.
5. С помощью метода опрокинутой характеристики определить ток в напряжения на элементах электрической цепа, состоящей из последовательно соединенных ламп накаливания и резистора R при условии, что цепь подключена к источнику питания с известным напряжением U (величина напряжения задается преподавателем). Графические построения провести на рис.9 в первом квадранте.
Контрольные вопросы и задачи
1. Какие элементы электрических цепей называются нелинейными? Приведите примеры нелинейных элементов.
2. Какую электрическую цепь называют нелинейной? Могут ли линейные элемента входить в нелинейную цепь?
3. В каком случае нелинейный элемент имеет симметричную АВХ? Приведите в виде графиков примеры симметричных АВХ известных вам элементов электрических цепей.
4. Начертите АВХ полупроводникового стабилитрона и охарактеризуйте ее с точки зрения симметрии.
5. Сформулируйте сущность метода сложения АВХ, применяемого при анализе нелинейных электрических цепей.
6. Сформулируйте сущность метода пересечения характеристик, применяемых при анализе нелинейных электрических цепей.
7. Какие две электрические величины должны быть известны для построения опрокинутой ВАХ резистора?
8. Как изменятся ток в электрической цепи (рис.4) и напряжения на элементах цепи, если увеличить величину сопротивления R?
Библиографический список
1. Электротехника / Под ред. В.Г. Герасимова. - М.: Высшая школа, 1985. -.137-144.
2. Волынский Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника. - М.: Энергоатомиздат, 1987. – С.190-200.
3. Борисов Ю.М., Дипатов Д.Н., Зорин Ю.Н. Электротехника. – М.: Энергоатомиздат, 1985. - С.50-54.
4. Касаткин а.С., Немцов М.В. Электротехника. - М.: Энергоатомиздат, 1983. - С.40-41, 208-213.
Протокол испытаний
к лабораторной работе №З. “Исследование нелинейных электрических цепей постоянного тока”.
Таблица 1
| Прямая ветвь ампер-вольтной характеристики | |||||
| UЛН, В | |||||
| IЛН, В | |||||
| Обратная ветвь ампер-вольтной характеристики | |||||
| UЛН, В | |||||
| IЛН, В |
Таблица 2
| Прямая ветвь ампер-вольтной характеристики | |||||
| IСТ = IR, A | |||||
| U, B | |||||
| UСТ, В | |||||
| UR, B | |||||
| Обратная ветвь ампер-вольтной характеристики | |||||
| IСТ = IR, A | |||||
| U, B | |||||
| UСТ, В | |||||
| UR, B |
Расчетно-графическая часть
Краткие выводы по работе:
Группа Студент Дата
Преподаватель
Лабораторная работа №4
Исследование индуктивной катушки и конденсатора
Цель работы
1. Получить навыки экспериментального определения параметров индуктивной катушки и конденсатора.
2. Освоить методы анализа электрической цепи синусоидального тока, состоящей из индуктивной катушки или конденсатора.
Основные теоретические положения
В данной работе исследуются отдельные элементы цепей синусоидального тока - индуктивная катушка с постоянными параметрами R и L (рис.1), а также конденсатор переменной емкости C (рис.2).
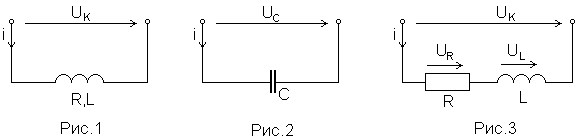При анализе цепи индуктивную катушку представляют в виде эквивалентной схемы замещения, представляющей собой последовательное соединение резистивного элемента с сопротивлением R, равным активному сопротивлению катушки и индуктивного элемента с индуктивностью L, раиной индуктивности катушки (рис.3).
Полное сопротивление катушки Z = Uк / I, где Uк и I – действующие значения напряжения и тока катушки. Полное сопротивление связано с сопротивлением схемы замещения следующей формулой:
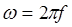
Где - индуктивное сопротивление катушки;
- угловая частота;
-
f - частота тока в цепи (f = 50 Гц).
Полное сопротивление катушки можно представить как гипотенузу прямоугольного треугольника сопротивлений (рис.4), один катет, которого равен R, а другой XL. Из треугольника сопротивлений следуют расчетные формулу:
В соответствии со вторым законом Кирхгофа вектор напряжения индуктивности катушки UK определяется выражением UK = UR + UL.
Вектор напряжения на резистивном элементе UR (активная составляющая вектора UК) совпадает по направлению с вектором тока I. Вектор напряжения на индуктивном элементе UL (реактивная составляющая вектора UК) опережает вектор тока I на угол 90°. Действующие значения напряжений UR и UL, тока I и соответствующие сопротивления катушки связаны следующими формулами: UR = RI, UL = XLI. Вектор напряжения индуктивной катушки UK опережает вектор тока I на угол jK(0< jK<90o). Векторная диаграмма тока и напряжений индуктивной катушки приведена на рис.5.
Векторы напряжений UK, UR, UL образуют треугольник напряжений, подобный треугольнику сопротивлений. Из треугольника напряжения можно составить следующие расчетные формулы:
Полная мощность катушки SK по определению равна произведению действующих значений напряжения на катушке UK и тока катушки I, т.е.
SK = UKI. Учитывая, что UK = ZKI, получаем SK = ZKI2.
Полная мощность SK связана с активной Р и реактивной QL мощностями индуктивной катушки выражением 
.
Активная мощность Р численно равна электрической энергии, преобразующейся в катушке в теплоту за единицу времени, и определяется формулами: 
.
Реактивная мощность QL численно равна амплитуде мгновенной мощности, находящейся в процессе обмена между магнитным полем катушки и источником электрической энергии. Величина реактивной мощности определяется формулами:
Графически связь между SK, P, QL можно представить в виде прямоугольного треугольника мощностей (рис.6), гипотенуза которого равна SK, а катеты P и QL. Треугольник мощностей подобен треугольникам сопротивлений и напряжений.
Из него вытекают следующие соотношения:
Величина соsj называется коэффициентом мощности, поскольку из треугольника мощностей соsj = P / S, т.е. он показывает, какую часть активная мощность P составляет от полной мощности S.
При исследовании конденсатора его представляют, пренебрегая потерями, в виде емкостного элемента, обладающего емкостью С.
Емкостное сопротивление конденсатора XC =UC / I, где UC и I - действующие значения напряжения и тока конденсатора.
 |
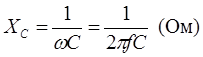Величина XC зависит от емкости конденсатора C и частоты протекающего в нем тока.
Векторная диаграмма тока и напряжения конденсатора приведена на рис.7. На ней видно, что вектор напряжения на емкостном элементе UC отстает от вектора тока I на угол 90o.
В электрической цепи с емкостным элементом работа не совершается, поэтому активная мощность Р, потребляемая емкостным элементом, равна нулю. Однако в цепи происходит периодический обмен энергией между источником и емкостным элементом. Интенсивность такого обмена характеризуют реактивной мощностью:
QC = UCI = XCI2.
Объект и средства исследования
Объектами исследования являются индуктивная катушка о постоянными параметрами R и L и батарея конденсаторов, емкость которой можно изменять с помощью переключателей П2. Емкость батареи равна сумме емкостей параллельно включенных в нее конденсаторов. Все элементы исследуемой цепи смонтированы на плате №10 передней панели стенда.
В качестве электроизмерительных приборов при исследовании применяются многопредельный миллиамперметр типа Э-377 и цифровой или стрелочный электронный вольтметр. В качестве источников питания используются: однофазный двухполупериодный выпрямитель со сглаживающим фильтром при питании катушки и конденсатора постоянным током и одна из фаз трехфазного источника при питании катушки и конденсатора переменным током.
Порядок проведения эксперимента
1. Исследование индуктивной катушки в цепи постоянного тока.
1.1. Собрать электрическую цепь согласно схеме, представленной на рис.6 протокола испытаний.
1.2. Установить на вольтметре режим измерения постоянного напряжения.
1.3. После проверки цепи преподавателем подать на нее напряжение, для чего выключатели В1(3~36 В), В2(-20 В) и ВЗ-1 (плата №3) поставить в положение "Вкл.", а выключатель ВЗ-2 (плата №3) - в положение П. Поворачивая ручку регулятора выходного напряжения выпрямителя (плата №3), установить значение напряжения на зажимах катушки в интервале 8 - 16 В.
1.4. Измерить по приборам постоянные напряжение Uпост и ток Iпост и записать их значения в табл.1 протокола испытаний.
1.5. Выключатели В1 и В2 выключить, полученные результаты согласовать с преподавателем.
2. Исследование индуктивной катушки в цепи переменного тока.
2.1. Собрать электрическою цепь согласно схеме, представленной на рис.9 протокола испытаний.
2.2. Установить на вольтметре режим измерения переменного напряжения.
2.3. После проверки цепи преподавателем подать на нее напряжение, для чего выключатель В1(3 ~36 в) поставить в положение "Вкл.".
2.4. Измерить по приборам действующие значения синусоидальных напряжения UK и тока I катушки и записать их в табл.1 протокола испытаний.
2.5. Выключить выключатель В1 и согласовать полученные результаты с преподавателем.
3. Исследование конденсатора в цепи постоянного тока.
3.1.Собрать электрическую цепь согласно схеме, представленной на рис.10 протокола испытаний.
3.2.Выполнить п.1.2 - 1.5, записав результаты измерений в табл.2 протокола испытаний.
4. Исследование конденсатора в цепи переменного тока.
4.1.Собрать электрическую цепь согласно схеме, представленной на рис.11 протокола испытаний.
4.2. Выполнить п. 2.2 – 2.3.
4.3. Изменяя емкость батареи конденсаторов с помощью переключателей П2 в пределах от 20 до 90 мкф, провести 5 измерений действующих значений тока I и напряжения UC. Результат измерений записать в табл.3 протокола испытаний.
4.4. Выполнить п.2.5.
Обработка результатов эксперимента
1. Вычислить значения параметров катушки, указанные в табл.4. Активное сопротивление катушки при этом найти по результатам исследования катушки на постоянном токе, т.е. R = Uпост / Iпост;
2. Построить на рис.12 (прил.) векторную диаграмму тока и напряжений на индуктивной катушке, выбрав масштабы по току mI и по напряжению mU.
3. Построить на рис.13 (прил.) треугольники сопротивлений и мощностей индуктивной катушки.
4. Используя экспериментальные данные (табл.3) вычислить в соответствии с законом Ома значения емкостных сопротивлений XC батареи конденсаторов и емкостей Cp, приняв частоту тока f = 50 Гц. Ре результаты записать в табл.5 (прил.).
5. Построить на рис.14 (прил.) векторную диаграмму тока и напряжения конденсатора, выбрав масштабы по току и напряжению.
6. По данным табл.3 построить на рис. 15 (прил.) график зависимости I(C).
Контрольные вопросы и задачи
1. Какими параметрами характеризуется индуктивная катушка?
2. Каким выражением связаны полное, активное и индуктивное сопротивления катушки?
3. Каким выражением связаны вектор напряжения на зажимах катушки и его активная и реактивная составляющие?
4. Каким выражением связаны полная, активная и реактивная мощности индуктивной катушки?
5. Какими параметрами характеризуется конденсатор?
6. Как можно определить емкостное сопротивление?
7. Какие мощности выделяются на конденсаторе при протекании через него синусоидального тока?
8. Активное сопротивление катушки равно 8 Ом, а ее коэффициент мощности равен 0,8. Чему равно индуктивное сопротивление катушки?
9. Емкость конденсатора равна 20 мкф. Чему равно емкостное сопротивление?
10. Емкость конденсатора равна 10 мкф. К его зажимам приложено постоянное напряжение 5 В. Какой ток будет протекать в цепи?
11. Активное и индуктивное сопротивления катушки равны. Чему равен угол сдвига фаз между напряжением и током катушки?
12. Активная мощность катушки равна 400 Вт, а ее активное сопротивление равно 100 Ом. Чему равна, активная составляющая напряжения катушки?
13. Активное и индуктивное сопротивления катушки соответственно равны 3 Ом и 4 Ом. Ее реактивная мощность равна 36 вар. Чему равно напряжение на зажимах катушки?
14. Полная мощность и ток катушки равны соответственно 80 В-А и 2 А. Угол сдвига фаз между напряжением и током катушки равен 60°. Чему равно активное сопротивление катушки?
15. Полная и активная мощности и активное сопротивление катушки равны соответственно 25 В-А, 20 Вт и 5 Ом. Чему равна реактивная составляющая напряжения катушки?
16. Активное сопротивление катушки в 2 раза меньше полного. Полная мощность катушки равна 1 кВ-А. Чему равна активная мощность катушки?
Библиографический список
1. Электротехника / Под ред. В.Г. Герасимова. - М.: Высшая школа, 1985. - С.59-66, 69-71.
2. Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника. - М.: Энергоатомиздат, 1985. - С.76-82, 86-89.
3. Волынский Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника – М.: Энергоатомиздат, 1987. - С.78-83.
Протокол испытаний
к лабораторной работе №4 "Исследование индуктивной катушки и конденсатора".
Таблица 1
| Uпост, В | Iпост, А | UK, B | I, A |
Таблица 3
| Таблица 2 | № опыта | ||||||
| Uпост, В | Iпост, А | С, мкф | |||||
| UC, В | |||||||
| I, A |
Расчетно-графическая часть
Таблица 4
| R, Ом | ZK, Ом | XL, Ом | L, Гн | jK, град | Соs jK | ||||
| UR, B | UL, B | P, Вт | QL, вар | S, B-A | |||||
Расчетные формулы:
Векторная диаграмма тока Треугольники сопротивле-
и напряжений катушки ний и мощностей катушки
mI= A / см; mU = B / см.
Рис.13
Таблица 5
| № опыта | |||||
| XC, Ом | |||||
| CP, мкф |
Краткие выводы по работе:
Группа Студент Дата
Преподаватель
Лабораторная работа №5
Исследование линейной неразветвленной электрической цепи синусоидального тока
Цель работы
1. Исследовать явление резонанса напряжения,
2. Установить связь между током, напряжениями на элементах цепи и емкостью конденсатора.
3. Получить навыки построения векторных диаграмм и научиться их использовать для анализа электрических цепей.
Основные теоретические положения.
В данной работе исследуется неразветвленная цепь, состоящая из катушки индуктивности и конденсатора и подключенная к сети синусоидального тока. Схема цепи представлена на рис.1.
 |
Реальная катушка индуктивности обладает кроме индуктивного сопротивления ХL еще и активным сопротивлением R, которое существенно влияет на протекающие в цепи процессы. Поэтому целесообразно реальную цепь представить в виде схемы замещения /рис.2/, где катушка индуктивности рассматривается как последовательное соединение резистивного элемента с активным сопротивлением R и индуктивного элемента с индуктивностью L. При этом падение напряжения на катушке UK равно сумме падений напряжений на резистивном элементе UR и индуктивном элементе UL.
 |
В соответствии с законом Ома полное сопротивление цепи Z=U/I. Индуктивный и емкостный элементы характеризуются соответственно индуктивным ХL и емкостным ХC сопротивлениями, определяемыми формулами:
где w - угловая частота питающего напряжения;
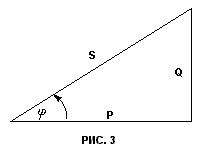
f - частота питающего напряжения /в данной работе f = 50 Гц./ Величина Х = ХL - ХC называется реактивным сопротивлением. Соотношение активного R, реактивного Х и полного Z сопротивлений определяется треугольником сопротивлений /рис.3/, откуда следует:
 |
 |
Вектор суммарного напряжения, т.е. напряжения источника
 |
Вектор напряжения на резистивном элементе UR /активная составляющая напряжения U /совпадает по направлению с вектором тока I. Действующее значение этого напряжения
 |
Вектор напряжения на индуктивном элементе U L / индуктивная составляющая напряжения U / опережает вектор тока I на 90°. Действующее значение этого напряжения.
Вектор напряжения на емкостном элементеUC /емкостная составляющая напряжения U / отстает от вектора тока на угол 90°. Действующее значение этого напряжения UC=XCI.
Возможны три различных соотношения параметров ХL и ХC
1. ХL>ХC, тогда UL>UC и вектор U опережает вектор I на угол j (рис.4)
2. ХL>ХC,тогда UL>UC и вектор U отстает от вектора I на угол j (рис.5) в любом из этих случаев |j| < 90°, т.к. UR неравно 0 /
3. ХL = ХC , тогда X=0, Z=R, UL=UC ,U=UR и вектор U совпадает по направлению с вектором I (рис. 6).
 |
Режим работы последовательной цепи синусоидального тока, при котором ток и общее напряжение цепи совпадают по фазе, что соответствует совпадению по направлению на векторной диаграмме векторов I и U, называется резонансом напряжений.
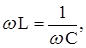Резонанс напряжений возникает при соблюдении следующего условия:
XL=XC или откуда
Таким образом, резонанс напряжений в цепи может быть получен за счет изменения одного из следующих параметров: индуктивности катушки L, емкости конденсатора С или частоты питающего напряжения f. В данной работе резонанс напряжений получают с помощью изменения емкости конденсатора.
 |
В режиме резонанса j = 0 полное сопротивление цепи Z принимает минимальное значение, равноеR, а следовательно, ток в цепи достигает максимума.
Напряжения на реактивных элементах UL и UC при резонансе имеют одинаковые действующие значения и противоположны по фазе, т.е. навекторной диаграмме векторы UL и UC имеют равную длину и направлены в противоположные стороны.
Полная мощность цепи S определяется ныражением S=U*I=Z*I2 и зависит от мощности, выделяемой на активных элементах цепи /активной мощности Р/ и реактивных элементах /реактивная мощность Q/. Величины S, P и Q связаны между собой как стороны треугольника мощностей /рис.7/, который аналогичен треугольнику сопротивлений.
 |
Для мощностей P, Q и S справедливы следующие соотношения:
Отношение R/Z или P/S, равное называют коэффициентом мощности цепи. По его величине судят о том, какую часть от полной мощности составляет активная мощность.
В режиме резонанса напряжений QL=QC, следовательно и полная мощность цепи равна активной мощности (SРЕЗ=РРЕЗ).
Объект и средства исследования
Объектом исследования служит последовательная цепь, включающая в себя индуктивную катушку с постоянными параметрами R и L, а также батарею конденсаторов, емкость которой меняется при помощи переключателей П2. Емкость батареи равна сумме емкостей параллельно включенных конденсаторов. Элементы исследуемой цепи смонтированы на плате 10 передней панели стенда.
В качестве электроизмерительных приборов применяется многопредельный миллиамперметр типа Э-З77 и электронный вольтметр (цифровой или стрелочный). Источником питания исследуемой цепи является одна из фаз трехфазного источника.
Порядок проведения эксперимента
1. Собрать электрическую цепь в соответствии со схемой, изображенной на рис.8 протокола испытаний. После проверки цепи преподавателем подать на нее напряжение, установив выключатель В1(3~36 B) в положение "Вкл".
2. Установить в цепи режим резонанса напряжений. Для этого необходимо постепенно увеличивать емкость батареи конденсаторов с помощью переключателей П2, наблюдая по амперметру за величиной тока I. Достижение током I максимально возможного значения свидетельствует о наступлении режима резонанса напряжений. Записать значения емкости, тока и напряжений при резонансном режиме в третью строку табл.1 протокола испытаний.
3. Провести опыты №1 и №2 при меньших значениях емкостей, чем в резонансном режиме, а опыты №4 и №5 при больших, значениях емкостей, чем в резонансном режиме. При проведении опытов нужно стремиться к тому, чтобы они охватывали как можно больший интервал изменения емкости батареи (примерно от 20 до 90 мкф). Полученные при этих опытах значения емкости, тока и напряжений записать в табл.1 протокола испытаний.
4. Согласовать с преподавателем результаты экспериментов, после чего разобрать электрическую цепь.
Обработка результатов эксперимента
1. Для каждого из опытов рассчитать значения активной мощности Р, полной мощности S, коэффициента мощности, полного сопротивления цепи Z, напряжений UR и UL. Активная мощность Р вычисляется по формуле Р = R*I2, где активное сопротивление R предварительно находится по закону Ома на основе экспериментальных данных резонансного режима (R=Uрез/Iрез) Рассчитанные значения записать в табл.2 (прил.).
2. По данным табл.2 построить на рис.9 /прил./ графики зависимостей I(C), Z(С), cos &(С)
3. Для двух опытов, назначенных преподавателем, построить
векторные диаграммы тока и напряжений на рис.10 и рис.11,
выбрав в соответствии с экспериментальными данными,
масштабы по току m I и по напряжению m v. Построение век
торных диаграмм рекомендуется осуществлять в следующем
порядке:
а) отложить вектор тока I в произвольном направлении;
б) отложить вектор индуктивной составляющей напряжения U L, опережающий вектор тока I на угол 90°;
в)из конца вектора U L, построить вектор активной составляющей напряжения U R, совпадающий по направлению с вектором тока I;
г) построить вектор напряжения U K как векторную сумму U L и U R;
д) из конца вектора U R построить вектор напряжения на конденсаторе U C, отстающий от вектора тока I на угол 90°;
е) построить вектор общего напряжения U,просуммировав векторы напряжений U K и U C .
Примеры векторных диаграмм приведены на рис. 4-6.
Контрольные вопросы и задачи
1. Укажите признаки наступления резонанса напряжений в последовательной цепи при изменении емкости конденсатора.
2. Какие векторы на векторной диаграмме имеют при резонансе напряжений одинаковую длину?
3. При каком условии возникает резонанс напряжений и почему?
4. Изобразите векторную диаграмму тока и напряжений в последовательной цепи при XL > XC.
5. Изобразите векторную диаграмму тока и напряжений в последовательной цепи при XL < XC.
6. Изобразите векторную диаграмму тока и напряжений в последовательной цепи при резонансе напряжений.
7. Активное сопротивление цепи равно емкостному и равно половине индуктивного сопротивления. Чему равен угол сдвига фаз между током и напряжением?
8. Полная мощность, коэффициент мощности и активное сопротивление цепи соответственно равны: 1 кВ*А; 0,8; 2 Ом. Чему равно действующее значение тока в цепи?
9. Полная мощность и реактивное сопротивление цепи соответственно равны 400 В*А и 2 Ом. Угол сдвига фаз, между током и напряжением равен 30. Чему равно действующее значение напряжения на зажимах цепи?
10. Активное и реактивное сопротивления и реактивная мощность цепи соответственно равны 3 Ом, 4 Ом, 36 вар. Чему равна полная мощность цепи?
11. Полное сопротивление, коэффициент мощности и напряжение цепи соответственно равны 10 Ом; 0,6; 20 В. Чему равна активная мощность цепи?
12. Сопротивление и мощность конденсатора соответственно равны 10 Ом, 90 вар. Индуктивная составляющая напряжения равна 50В. Чему равна реактивная мощность цепи?
13. Активная, индуктивная и емкостная мощности цепи соответственно равны 6 Вт, 10 вар и 2 вар. Чему равен коэффициент мощности цепи?
14. Ток и полная мощность цепи соответственно равны 2 А и 36 В*А. Чему равно активное сопротивление цепи, если в ней имеет место резонанс напряжений?
15. Напряжение, ток и сдвиг фаз между ними соответственно равны 200 В, 10 А, 37°. Чему равно реактивное сопротивление цепи?
Библиографический список
1. Электротехника / Под ред. В.Г. Герасимова. – М.: Высшая школа, 1985. – С.59-65, 69-73, 81-86.
2. Волынский Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника. – М.: Энергоатомиздат, 1987. – С.83-92, 116-119.
Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника. – М.: Энергоатомиздат, 1985. - С.84-95.
Протокол испытаний
к лабораторной работе №5 "Исследование линейной неразветвленной электрической цепи синусоидального тока"
 |
Таблица 1
| Номер опыта | С, мкФ | I, mA | U, B | UK, B | UC, B |
Расчетно-графическая часть
Таблица 2
| Номер опыта | P,Bт | S, B*A | cosф | Z,Ом | UR, B | UL, B |
Расчетные формулы:
 |
Векторные диаграммы (mI= A/cm; mV= B/cm)
 |
а) для опыта №_____ б) для опыта №_____
Краткие выводы по работе:
Группа____________Студент______________Дата________
Преподаватель___________________________
Лабораторная работа №6
Исследование линейной разветвленной электрической цепи синусоидального тока.
Цель работы:
1. Исследовать явление резонанса токов.
2. Установить связь токов в цепи с емкостью конденсатора.
3. Получить навыки построения векторных диаграмм и научиться их использовать для анализа электрических цепей.
Основные теоретические положения
В данной работе исследуется разветвленная электрическая цепь, состоящая из параллельно соединенных катушки индуктивности и конденсатора, и подключенная к источнику синусоидального напряжения. Схема цепи представлена на рис.1.
Так как реальная катушка индуктивности обладает активным сопротивлением, ее целесообразно представить в виде эквивалентной схемы замещения. В отличие от работы №5 в данном случае удобнее воспользоваться параллельной схемой замещения катушки индуктивности, где параллельно включены резистивный элемент с активной проводимостью G и индуктивный элемент с индуктивной проводимостью BL /рис.2/. Конденсатор обладает емкостной проводимостью ВC.
 |
Активная и реактивная проводимости связаны с соответствующими сопротивлениями следующими соотношениями:
В соответствии с законом Ома полная проводимость цепи Y=I/U, а полная проводимость катушки индуктивности YK=IK/U.
Соотношение активной G,реактивной В=ВL-BC и полной Y проводимостей определяется треугольником проводимостей для всей цепи /рис.3/, откуда следует:
Аналогично из треугольника проводимостей для катушки -/рис.4/
 |
В соответствии с первым законом Кирхгофа
I = I K + I C = I ak + I pk + I c
 |
Вектор активной составляющей тока катушки I ak совпадает по направлению с вектором напряжения U. Действующее значение активной составляющей
Вектор реактивной составляющей тока катушки I pk отстает от вектора напряжения U на 90°. Действующее значение реактивной составляющей
 |
Вектор тока конденсатора Iс опережает вектор напряжения на 90°.
Действующее значение этого тока Iс=ВCU.
Действующее значение общего тока I в цепи и угол j сдвига фаз
 |
между общим током и напряжением определяются соотношениями:
Возможны три различных соотношения параметров BL и ВC.
1. BL > ВC, тогда Iрк > IC и вектор тока I отстает от вектора напряжения U на угол j (рис.5).
2. BL < ВC, тогда Iрк < IC и вектор тока I опережает вектор напряжения U на угол j (рис.6).
3. BL = ВC, тогда Iрк = IC, В =0, Y=G, I=Iak и вектор I совпадает по направлению с вектором U (рис.7).
Режим работы параллельной цепи синусоидального тока, при котором напряжение и общий ток совпадают по фазе, что соответствует совпадению по направлению векторов U и I на векторной диаграмме, называется резонансом токов.
Условием резонанса является равенство индуктивной и емкостной проводимостей параллельных ветвей, т.е. ВL= ВC.
Режима резонанса токов можно достичь путем изменения одного из следующих параметров: индуктивности катушки L, емкости конденсатора С, активного сопротивления катушки R или частоты питающего напряжения f. В данной работе резонанс токов получают путем изменения емкости конденсатора.
 |
При резонансе токов = 0, полная проводимость цепи Y принимает минимальное значение, равное G, а следовательно, минимальным будет и общий ток
Реактивная составляющая тока катушки iрк и ток конденсатора ic при резонансе токов имеют одинаковые действующие значения и отличаются по фазе на 180°, т.е. на векторной диаграмме векторы I kp и I C имеют равную длину и противоположно направлены.
Полная мощность всей цепи S и полная мощность катушки SK определяются соответственно выражениями:
В режиме резонанса токов QL = QC, т.е. Q = 0 и полная мощность цепи равна активной мощности (SРЕЗ= PРЕЗ).
Объект и средства исследования
Объектом исследования служит разветвленная цепь, состоящая из параллельно включенных индуктивной катушки с неизменными параметрами и батареи конденсаторов, емкость которой можно менять при помощи переключателей. Емкость батареи равна сумме емкостей конденсаторов, включенных параллельно. Элементы исследуемой цепи смонтированы на плате №10 передней панели стенда.
В качестве электроизмерительных приборов используются многопредельный миллиамперметр Э-377 и электронный вольтметр /цифровой или стрелочный/. Питание исследуемой цепи осуществляется линейным напряжением трехфазного источника.
Порядок проведения эксперимента
1. Собрать электрическую цепь в соответствии со схемой, изображенной на рис.8 протокола испытаний. После проверки цепи преподавателем подать на нее напряжение, установив выключатель В1(3~36 В) в положение "Вкл.".
2. Установить в цепи режим резонанса токов. Для этого необходимо постепенно увеличивать емкость батареи конденсаторов с помощью переключателей П2, наблюдая по амперметру за величиной общего тока. Минимальное значение общего тока I свидетельствует о наступлении режима резонанса токов. Записать значения емкости, токов и напряжения при резонансном режиме в третью табл.1 протокола испытаний.
3. Провести опыты№1 и №2 при меньших значениях емкостей, а опыты №4 и №5 при больших значениях емкостей, чем в резонансном режиме. При проведении опытов следует стремиться к тому, чтобы охватить как можно больший интервал изменения емкости батареи конденсаторов. Полученные при этих опытах значения емкости, токов и напряжения записать в табл.1 протокола испытаний.
4. Согласовать с преподавателем результаты экспериментов, после чего разобрать электрическую цепь.
Обработка результатов эксперимента
1. Для каждого из опытов рассчитать активную мощность Р, полную мощность S, коэффициент мощности соs j и полную проводимость Y. Активная мощность Р вычисляется по формуле Р = GU2, где активная проводимость G предварительно находится по формуле: G = IРЕЗ/UРЕЗ. Рассчитанные значения записать в табл.2 (прил.).
2. По данным табл.2 построить на рис.9 /прил./ графики зависимостей I(С), Y(С), cos j (С).
3. Для двух опытов, назначенных преподавателем, построить векторные диаграммы токов и напряжения на рис.10 и рис.11, выбрав в соответствии с экспериментальными данными масштабы для векторов токов mI и напряжения mV. Построение векторных диаграмм рекомендуется осуществлять в следующем порядке:
а) отложить вектор напряжения U в произвольном направлении;
б) отложить вектор активной составляющей тока катушки индуктивности I AK совпадающий по направлению с вектором напряжения U. Действующее значениеIAK=IPE3.
 |
в) отложить вектор реактивной составляющей тока катушки индуктивности I PK, отстающий от вектора напряжения U на угол 90°. Действующее значение:
г) построить вектор I K, как векторную сумму I AK и I PK;
д) отложить вектор тока конденсатора I C, опережающий вектор напряжения U на угол 90°;
е) построить вектор общего тока I, просуммировав векторы I K и I C. Примеры векторных диаграмм приведены на рис.5-7.
Контрольные вопросы и задачи
1. Укажите признаки наступления резонанса токов в параллельной цепи при изменении емкости конденсатора.
2. Какие векторы на векторной диаграмме имеют при резонансе токов одинаковую длину?
3. При каком условии возникает резонанс токов и почему?
4. Изобразите секторную диаграмму напряжения и токов в параллельной цепи при BL > ВC.
5. Изобразите векторную диаграмму напряжения и токов в параллельной цепи при BL < ВC.
6. Изобразите векторную диаграмму напряжения и токов в параллельной цепи при резонансе токов.
7. Полная мощность цепи, проводимость и ток емкостной ветви соответственно равны: 200 В*А, 0,04 См, 2 А. Чему равна полная проводимость цепи?
8. Активная мощность и ток цепи соответственно равны 100 Вт и 10 А. Угол сдвига фаз между током и напряжением равен 60 градусов. Чему равна активная проводимость цепи?
9. Полная и реактивная мощности цепи соответственно равны 1 кВ*А и 600 вар. Активная составляющая общего тока цепи равна 16 А. Чему равна реактивная проводимость цепи?
10. Ток катушки равен 6 А и отстает по фазе от напряжения на 37°. Чему равен общий ток цепи, если он опережает напряжение на 53°?
11. Напряжение на зажимах цепи, активная проводимость и реактивная мощность катушки соответственно раины: 100В, 0,06 См, 800 вар. Чему равен ток катушки?
12. Общий ток цепи равен 1А и совпадает по фазе с напряжением. Ток катушки отстает от напряжения по фазе на угол 45°. Чему равен ток емкостной ветви?
13. Полная мощность, полная и реактивная проводимости цепи соответственно равны: 200 В*А, 0,5 См, 0,4 См. Чему равна активная составляющая тока катушки?
14. Полная мощность катушки, проводимость и ток емкостной ветви соответственно равны: 800 В*А, 0,1 См, 10 А. Ток катушки отстает по фазе от напряжения на угол 30°. Чему равна реактивная составляющая тока катушки?
15. Активная проводимость катушки, мощность и проводимость емкостной ветви соответственно равны: 0,3 См, 40 вар, 0,4 См. В цепи имеет место резонанс токов. Чему равна полная мощность катушки?
Библиографический список
1. Электротехника / Под ред. В.Г. Герасимова - М.: Высшая школа, 1985. - С.73-77.
2. Волынский Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника. - Энергоатомиздат, 1987, - С.94-100, 120-123.
3. Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника.
Энергоатомиздат, 1985. - С.95-105.
4. Касаткин А.С., Немцов М.В. Электротехника. - Энергоатомиздат, 1983. - С.84-88. 92-98.
Протокол испытаний
к лабораторной работе №6 "Исследование линейной разветвленной электрической цепи синусоидального тока"
 |
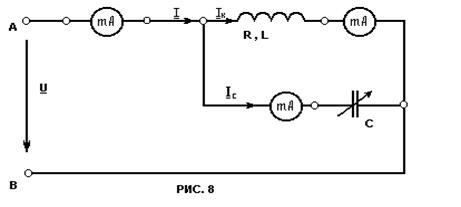Таблица 1
| Номер Опыта | С,мкФ | I, mA | IK, mA | Ic, mA | U, B |
Таблица 2
| Номер Опыта | P,Bт | S, B*A | cosф | Y,Cм |
Расчетные формулы:
 |
Векторные диаграммы (mV=______B/Cm; mI=_______A/Cm)
a) для опыта №_____ б) для опыта №_______
 |
Краткие выводы по работе:
Группа____________Студент_____________ Дата________ Преподаватель________________________
Лабораторная работа №7
Исследование трехфазной электрической цепи с активной нагрузкой, соединенной по схеме “звезда”.
Цель работы:
1. Исследовать свойства трехфазной цепи с симметричной и несимметричной нагрузкой, соединенной “звездой”.
2. Оценить влияние нейтрального привода при различных режимах работы.
3. Освоить методы анализа трехфазных цепей с помощью векторных диаграмм.
Основы теории
 |
Трехфазная электрическая цепь включает в себя источник и потребитель трехфазной энергии, соединенные проводами. Источник трехфазной электрической энергии может быть представлен в виде совокупности трех однофазных источников синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых друг относительно друга по фазе на угол 120°, т.е. на 1/3 периода.
При использовании схемы соединения “звезда” концы фаз генератора X, Y, Z или приемникаx, y, z соединяются в общую точку, называемую нейтральной точкой, а начала фаз генератора А,В,С и приемника а, b, c подключаются к линейным проводам, соединяющим источник с потребителем. Нейтральные точки генератора и приемника n соединены нейтральным проводом. При наличии нейтрального провода трехфазная цепь называется четырехпроводной, а при его отсутствии - трехпроводной.
Напряжение между началом и концом каждой фазы генератора и приемника называется фазным напряжением генератора или приемника и обозначается UA, UB, UC -для генератора, Ua, Ub, Uc - для приемника.
Напряжение между началами разных фаз или между линейными проводами называются линейными напряжениями.
Токи, протекающие по фазам приемника или генератора, называются соответственно фазными токами приемника или генератора, а токи в линейных проводах называются линейными токами. На рис.1 представлена схема трехфазной цепи.
 |
Поскольку при соединении "звездой" приемники включаются последовательно с линейными проводами, фазные токи приемников равны линейным токам (Iфл = IЛ).
 |
На основании первого закона Кирхгофа I N= I a+ I b+ I c.Фазные напряжения генератора U A, U B, U C равны соответствующим ЭДС (внутренние сопротивления источников полагаем равными нулю).
где U фr - действующее значение фазного напряжения генератора. В соответствии со вторым законом Кирхгофа
U AB= U A- U B; U BC= U B- U C; U CA= U C- U A.
На риc. 2 представлена векторная топографическая диаграмма фазных напряжений генератора и линейных напряжений, которые образуют жесткую симметричную систему, не за
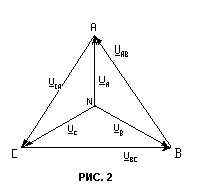висящую от нагрузки. Из диаграммы следует, что действующие значения всех линейных напряжений одинаковы
U AB= U BC- U CA= U Л
 |
и что фазные напряжения генератора и линейные напряжения находятся в соотношении
При наличии нейтрального провода потенциал точек n и N одинаковы и, следовательно, фазные напряжения приемника равны фазным напряжениям генератора, т.е.
U a= U A; U b= U B; U c= U C
Нагрузка, подключенная к трехфазной сети, может быть симметричной и несимметричной. При симметричной нагрузке комплексные сопротивления всех фаз приемника одинаковы,
т.е. Z a= Z b= Z c
Вследствие равенства комплексных сопротивлений фаз приемника действующие значения токов в фазах одинаковы (Ia=Ib=Ic), а векторы токов направлены под углом 120° друг относительно друга. Векторная диаграмма напряжений и токов для симметричной нагрузки представлена на рис. 3. Если в качестве приемников используются резисторы, векторы токов в фазах приемника совпадают по направлению с векторами фазных напряжений. Ток в нейтральном проводе, определяемый как векторная сумма фазных токов будет равен нулю т.к. векторы фазных токов образуют симметричную тройку векторов. Таким образом, при симметричной нагрузке надобность в нейтральном проводе отпадает.
При несимметричной нагрузке режим работы цепи будет различным в зависимости от наличия или отсутствия нейтрального провода. В четырехпроводной цепи, т.е. с нейтральным проводом обеспечивается симметрия фазных напряжений приемника вследствие их равенства фазным напряжениям генератора, следовательно
 |
Векторы фазных токов не будут симметричными вследствие различия сопротивлений в фазах, что приводит к возникновению тока в нейтральном проводе. Векторная диаграмма напряжений и токов для четырехпроводной цепи при несимметричной нагрузке представлена на рис.4. Векторы фазных токов совпадают с векторами соответствующих фазных напряжений вследствие активного характера нагрузки. Ток I N в нейтральном проводе строится как векторная сумма фазных токов. Если при несимметричной нагрузке отключить нейтральный провод, то в полученной трехпроводной цепи нарушится равенство потенциалов нейтральных точек генератора и приемника и между ними возникнет разность потенциалов UnN, называемая напряжением смещения нейтрали.
Векторная диаграмма напряжений и токов для трехпроводной цепи при несимметричной нагрузке представлена на рис.5. 
Положение нейтральной точки приемника на векторной топографической диаграмме может быть определено графически по экспериментальным значениям фазных напряжений приемника Ua, Ub, Uc. Для этого из вершин треугольника АВС, образуемого векторами линейных напряжений, необходимо провести дуги радиусами, равными в выбранном масштабе фазным напряжениям приемника Ua, Ub, Uc. Точка пересечения дуг укажет положение точки n. Векторы, соединяющие точку n с вершинами треугольника, являются векторами фазных напряжений приемника U a, U b, U c. Они связаны с фазными напряжениями генератора U А, U<
