В данной работе исследуются электрические цепи, в состав которых входят лампа накаливания (нелинейный элемент) и полупроводниковый стабилитрон (нелинейный элемент), последовательно соединенный с резистором (линейный элемент). Элемент электрической цепи, сопротивление которого зависит от тока или напряжения, называют нелинейным элементом. Нелинейной электрической цепью называют такую цепь, в состав которой входит хотя бы один нелинейный элемент.
При анализе нелинейных цепей электрические свойства нелинейных и линейных элементов представляют ампер-вольтными характеристиками (АВХ), которые отображают зависимость тока от напряжения I(U). АВХ линейных элементов имеют вид прямых линий, а нелинейных элементов - некоторых кривых линий.
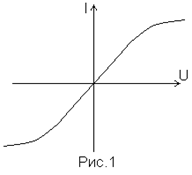По виду АВХ различают нелинейные элементы с симметричной и несимметричной характеристиками (по отношению к началу координат). Лампы накаливания облачают симметричными АВХ (рис.1). Нелинейность их характеристик обусловлена тем обстоятельством, что при повышении температуры сопротивление нити накаливания будет увеличиваться.
Полупроводниковый стабилитрон имеет несимметричную АВХ (кривая I (Uст) на рис.3).
При расчетах нелинейных цепей постоянного тока наиболее часто используют графические методы. Последовательные нелинейные цепи с двумя элементами можно рассчитывать двумя методами: 1)методом сложении АВХ элементов цепи; 2)методом пересечения АВХ элементов цепи.
Метод сложения АВХ рассмотрим на примере цепи, состоящей из полупроводникового стабилитрона VDи резистора R (рис.2). В единых осях координат строят АВХ стабилитрона I(Uст), резистора I(UR) и АВХ всей цепи (суммарную АВХ), представляющую собой зависимость тока I от общего напряжения U(кривая I(U) на рис.3). Построение этой кривой осуществляется путем сложения абсцисс АВХ стабилитрона и резистора для ряда фиксированных значений тока. При этом на графике получают ряд точек,
 |
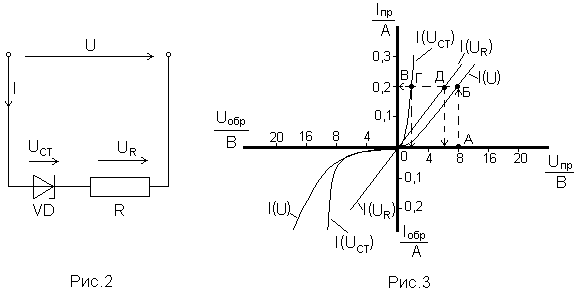соединение которых дает искомую кривую I(U).
После построения кривой I(U) на плоскости координат будут иметься в наличии три кривые, использование которых позволяет для данной цепи решать различные задачи. Например: дано напряжение U = 8 В, требуется определить ток в цепи и падения напряжений на элементах. Данная задача решается следующим образом. Из точки А, абсцисса которой равна 8 В, восстанавливают перпендикуляр к оси V до его пересечения с кривой I(U) в точке Б. Затем, опустив перпендикуляр из точки Б на ось I, получают точку В, которая указывает значение искомого тока I (в рассматриваемом примере I = 0,20 А). Прямая БВ пересекает характеристики I(Uст) и I(UR) в точках Г и Д, абсциссы которых равны искомым падениям напряжений на стабилитроне и резисторе соответственно (в рассматриваемом примере Uст = 1,8 В, UR = 6,2 В).
Метод пересечения характеристик удобно применять для решения частной задачи, когда один из элементов последовательной цепи является линейным элементом (резистором), заданы напряжение на зажимах цепи и сопротивление резистора, требуется определить той и падения напряжений на элементах цепи. Данный метод рассматривается на примере последовательной цепи, состоящей из лампы накаливания ЛН и резистора R (рис.4). Расчет цепи этим методом состоит в следующем.
В единых осях координат строят АВХ лампы накаливания I(Uлн) и опрокинутую АВХ резистора I(UR)опр. (рис.5). Опрокинутая характеристика (прямая АБ) строится по заданным значениям напряжения U и сопротивления R. В данном примере прямая АБ построена при условии, что U = 16 В, R = 20 Ом. Абсцисса точки А равна, заданному напряжению U, т.е. 16 В. Ордината точки Б определяется как частное от деления U на R, т.е. ордината точки Б равна U / R = 16 / 20 = 0,8 А.
 |
Прямая АБ и кривая I(Uлн) пересекаются в точке В, которая определяет решение задачи. Ордината точки В равна искомому току. В данной задаче I =0,6 А. Абсцисса точки В (точка Г на оси напряжений) определяет значения падений напряжений на лампе накаливания (отрезок ОГ) и на резисторе (отрезок ГА). В данном примере Uлн = 4 В, UR = 12 В.
