Изучая дисперсию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в расчетах, нельзя оценить влияние отдельных факторов, определяющих колеблемость индивидуальных значений (вариант) признака. Необходимо с помощью метода группировок подразделить изучаемую совокупность на однородные группы по факторному признаку. При этом кроме общей средней для всей совокупности надо исчислить средние по отдельным группам и три показателя дисперсии: общую дисперсию, межгрупповую дисперсию и среднюю внутригрупповую дисперсию.
Общая дисперсия характеризует вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:
| Простая | Взвешенная |

| 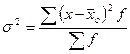
|
где  - общая средняя арифметическая для всей изучаемой совокупности.
- общая средняя арифметическая для всей изучаемой совокупности.
Межгрупповая дисперсия (дисперсия групповых средних) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под действием факторного признака, положенного в основу группировки:
| Простая | Взвешенная |

| 
|
где  - средняя по каждой группе.
- средняя по каждой группе.
Средняя внутригрупповая дисперсия характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от факторного признака, положенного в основу группировки:
| Простая | Взвешенная |

| 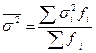
|
где 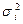 - дисперсия по каждой группе.
- дисперсия по каждой группе.
Указанные дисперсии взаимосвязаны между собой: величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии (это правило сложения дисперсий):
 .
.
В статистическом анализе широко используется такой показатель как коэффициент детерминации – это отношение межгрупповой дисперсии к общей дисперсии:
 .
.
Этот коэффициент показывает долю (удельный вес) общей вариации изучаемого признака, обусловленную вариацией группировочного (факторного) признака.
Корень квадратный из коэффициента детерминации называется корреляционным отношением:  .Он показывает влияние признака, положенного в основу группировки, на вариацию результативного признака (т.е. степень тесноты связи между признаками). Изменяется в пределах от 0 до 1. Если
.Он показывает влияние признака, положенного в основу группировки, на вариацию результативного признака (т.е. степень тесноты связи между признаками). Изменяется в пределах от 0 до 1. Если  , то группировочный признак не оказывает влияния на результативный. Если
, то группировочный признак не оказывает влияния на результативный. Если  , то результативный признак изменяется только в зависимости от признака, положенного в основу группировки, а влияние прочих факторных признаков равно нулю. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям по таблице Чеддока:
, то результативный признак изменяется только в зависимости от признака, положенного в основу группировки, а влияние прочих факторных признаков равно нулю. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям по таблице Чеддока:
| 0,1 - 0,3 0,3 - 0,5 0,5 - 0,7 0,7 - 0,9 0,9 - 0,99 | связь слабая умеренная заметная сильная очень (весьма) сильная |






