Если последовательность 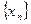 сходится, то она имеет единственный предел.
сходится, то она имеет единственный предел.
Доказательство:
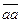 . Пусть последовательность
. Пусть последовательность 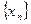 имеет два предела, т.е.
имеет два предела, т.е. 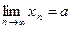 ,
, 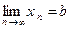 ,
, 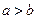 для определенности. Так как
для определенности. Так как 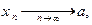 то имеет место соотношение (**), т.е. начиная с некоторого номера
то имеет место соотношение (**), т.е. начиная с некоторого номера 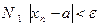 . Так как
. Так как 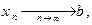 то выполняется (**), т.е. начиная с некоторого номера
то выполняется (**), т.е. начиная с некоторого номера 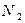
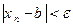 . Пусть
. Пусть 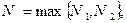 тогда, начиная с номера
тогда, начиная с номера 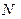
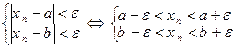 . Пусть
. Пусть 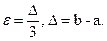 Тогда пересечение этих двух множеств, задаваемых неравенствами, пусто, т.е. нашлось, по крайней мере, одно
Тогда пересечение этих двух множеств, задаваемых неравенствами, пусто, т.е. нашлось, по крайней мере, одно 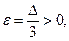 для которого не выполняется (**). Это означает, что предела не существует. +
для которого не выполняется (**). Это означает, что предела не существует. +
Теорема 2. Теорема Вейерштрасса - необходимое условие сходимости
Если последовательность сходится, то она ограничена.
Доказательство:
Пусть последовательность 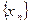 сходится, тогда имеет место соотношение (**), т.е. начиная с некоторого номера
сходится, тогда имеет место соотношение (**), т.е. начиная с некоторого номера 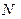 ,
, 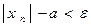 . Положим
. Положим 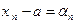 , тогда
, тогда 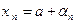 . Рассмотрим
. Рассмотрим  ,т.е.
,т.е. 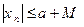 ,что озна- чает ограниченность последовательности
,что озна- чает ограниченность последовательности 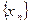 . +
. +
Теорема 3. Признак Больцано-Вейерштрасса.
Если последовательность монотонно возрастает (убывает) и ограничена сверху(снизу), то она сходится.
Доказательство:
Пусть последовательность 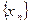 монотонно возрастает (
монотонно возрастает (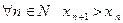 ) и ограничена (
) и ограничена (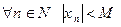 ). Тогда из условия ограниченности следует, что
). Тогда из условия ограниченности следует, что 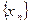 - непустое ограниченное сверху множество. Следовательно, по теореме о ТВГ (глава III, п. 4) множество
- непустое ограниченное сверху множество. Следовательно, по теореме о ТВГ (глава III, п. 4) множество 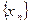 , значит, и последовательность
, значит, и последовательность 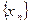 имеет ТВГ.
имеет ТВГ.
Обозначим 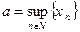 и покажем, что
и покажем, что 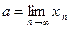 .
.
В силу определения ТВГ имеем 
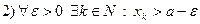 . Кроме того, последова- тельность
. Кроме того, последова- тельность 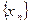 монотонно возрастает, поэтому найдется такой номер
монотонно возрастает, поэтому найдется такой номер 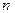 , что
, что 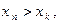 т.е.
т.е. 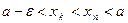 . Следовательно,
. Следовательно, 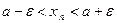 или
или 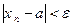 . Таким образом, существует такой номер
. Таким образом, существует такой номер 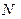 , начиная с которого
, начиная с которого 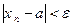 . +
. +
Пример. Последовательность 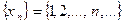 монотонно возрастает, но не ограничена, следовательно,
монотонно возрастает, но не ограничена, следовательно, 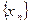 расходится.
расходится.
Пример. Последовательность 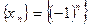 ограничена, но не является монотонной, следовательно, расходится.
ограничена, но не является монотонной, следовательно, расходится.
Пример. Пусть 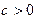 и
и 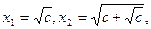
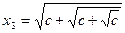 ,... или
,... или 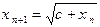 (*). Последовательность
(*). Последовательность 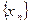 монотонно возрастает и ограничена сверху, например, числом
монотонно возрастает и ограничена сверху, например, числом 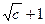 . Покажем это ММИ.
. Покажем это ММИ.
Пусть 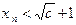 . Тогда
. Тогда 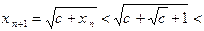
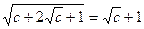 . Тогда существует
. Тогда существует 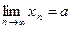 . Возведем (*) в квадрат и перейдем к пределу при
. Возведем (*) в квадрат и перейдем к пределу при 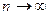 :
:  , т.е.
, т.е. 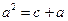 . Таким образом,
. Таким образом, 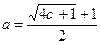 .
.
п. 4 Арифметические свойства пределов
Теорема 1. Пусть последовательности 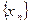 и
и 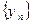 сходятся, тогда сходится и последовательность
сходятся, тогда сходится и последовательность 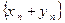 , причем
, причем 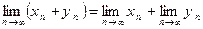 .
.
Доказательство:
Так как 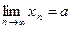 и
и 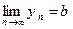 , то
, то 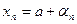 ,
, 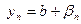 , где
, где 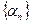 и
и 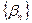 - БМП. Рассмотрим
- БМП. Рассмотрим 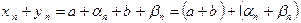 , причем
, причем 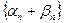 - БМП. Следовательно,
- БМП. Следовательно, 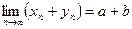 . +
. +
Следствие. Сумма любого конечного числа сходящихся последовательностей, является сходящейся последовательностью, предел которой равен сумме соответствующих пределов.
Теорема 2. Если 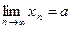 ,
, 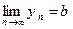 (пределы последовательностей xп и yп равны a и b соответственно), то
(пределы последовательностей xп и yп равны a и b соответственно), то 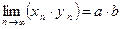 .
.
Доказательство:
В силу определения предела последователь- ности имеем 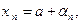
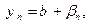 где
где 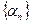 ,
, 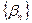 - БМП. Рассмотрим
- БМП. Рассмотрим 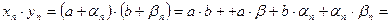
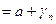 , при этом
, при этом 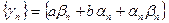 - БМП. Следовательно,
- БМП. Следовательно, 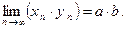 +
+
Теорема 3. Если пределы последовательностей xп и yп равны a и b соответственно для любого натурального числа n и yп ≠ 0, b≠ 0 (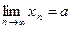 ,
, 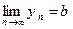
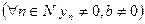 ), то
), то 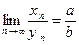 .
.
Доказательство:
Докажем сначала лемму.
Лемма. Если последовательность 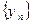 сходится
сходится 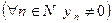 , то последовательность
, то последовательность 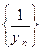 - ограничена.
- ограничена.
Пусть 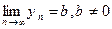 . Тогда имеет место соотношение (**). Пусть в (**)
. Тогда имеет место соотношение (**). Пусть в (**) 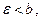 т.е.
т.е. 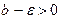 . Тогда существует номер
. Тогда существует номер 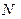 , начиная с которого
, начиная с которого 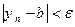 или
или 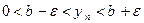 . Следовательно,
. Следовательно, 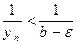 или
или 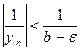 . Пусть
. Пусть 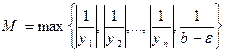 . Тогда
. Тогда 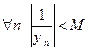 . ▲
. ▲
Рассмотрим 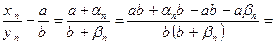
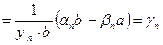 . Так как
. Так как 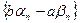 - БМП, а
- БМП, а 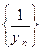 - ограничена, то
- ограничена, то 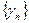 - БМП. Таким образом,
- БМП. Таким образом, 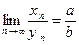 . +
. +
п. 5 Свойства пределов, связанные с неравенствами
Теорема 1. Пусть 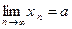 . Тогда, если найдется номер
. Тогда, если найдется номер 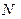 , начиная с которого
, начиная с которого 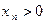 , то
, то 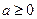 .
.
Доказательство:
Так как 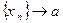 , то для нее имеет место соотношение (**). Предположим противное, т.е. пусть
, то для нее имеет место соотношение (**). Предположим противное, т.е. пусть 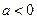 . Тогда из соотношения (**) имеем
. Тогда из соотношения (**) имеем 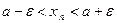 . Так как
. Так как 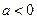 , то можно выбрать такое
, то можно выбрать такое 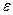 , что
, что 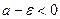 и
и 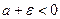 . Тогда, начиная с некоторого номера, определяемого этим
. Тогда, начиная с некоторого номера, определяемого этим 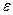 ,
, 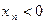 , что противоречит условию.
, что противоречит условию.
Следствие 1. Пусть 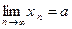 и существует такой номер
и существует такой номер 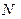 , начиная с которого
, начиная с которого 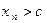 . Тогда
. Тогда  .
.
Доказательство:
Рассмотрим 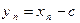 . Последовательность
. Последовательность 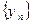 сходится. Более того, начиная с некоторого номера
сходится. Более того, начиная с некоторого номера 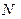
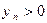 . Тогда
. Тогда 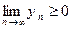 . Но
. Но 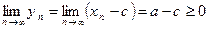 . Следовательно,
. Следовательно,  . +
. +
Следствие 2. Пусть 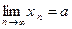 и, начиная с некоторого номера
и, начиная с некоторого номера 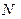 ,
, 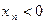 . Тогда
. Тогда 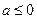 .
.
Следствие 3. Пусть 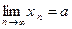 и, начиная с некоторого номера
и, начиная с некоторого номера 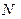 ,
, 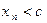 . Тогда
. Тогда 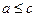 .
.
Теорема 2. Пусть 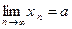 , причем
, причем 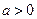 . Тогда существует такой номер
. Тогда существует такой номер 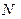 , что
, что 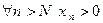 .
.
Доказательство:
Так как 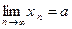 , то имеет место соотношение (**), т.е.
, то имеет место соотношение (**), т.е. 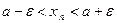 . Имеем
. Имеем 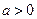 , выберем
, выберем 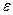 таким, чтобы
таким, чтобы 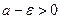 . Тогда найдет такой номер
. Тогда найдет такой номер 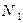 , начиная с которого,
, начиная с которого, 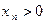 . +
. +
Следствие 1. Пусть 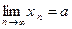 , причем
, причем 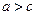 . Тогда существует такой номер
. Тогда существует такой номер 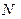 , начиная с которого,
, начиная с которого, 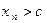 .
.
Следствие 2. Пусть 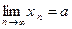 , причем
, причем 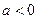 . Тогда существует такой номер
. Тогда существует такой номер 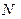 , начиная с которого,
, начиная с которого, 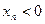 .
.
Следствие 3. Пусть 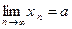 , причем
, причем 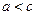 . Тогда существует такой номер
. Тогда существует такой номер 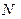 , начиная с которого,
, начиная с которого, 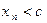 .
.






