Швидкість 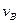 є початковою швидкістю для руху тягаря на ділянці ВС. Далі необхідно розглянути рух матеріальної точки на цій ділянці: прикласти всі діючі сили, скласти диференціальне рівняння руху точки і двічі проінтегрувати його з урахуванням початкових умов:
є початковою швидкістю для руху тягаря на ділянці ВС. Далі необхідно розглянути рух матеріальної точки на цій ділянці: прикласти всі діючі сили, скласти диференціальне рівняння руху точки і двічі проінтегрувати його з урахуванням початкових умов:
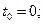
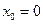 ;
; 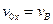 .
.
При інтегруванні диференціальних рівнянь руху у випадках залежності сили опору 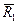 від
від 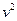 можна скористатись перетворенням:
можна скористатись перетворенням:
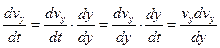 .
.
За правильне розв’язання задачі Д.1 з використанням даних таблиці 1. Умови задач Д.1.0 – Д.1.9 виставляється оцінка три бали; за правильне розв’язання задачі з використанням даних таблиці 2. Умови задач Д.1.0.А – Д.1.9.А виставляється оцінка чотири бали; за правильне розв’язання задачі з використанням даних таблиці 3. Умови задач Д.1.0.Б – Д.1.9.Б виставляється оцінка п’ять балів.
Приклад розв’язання задачі Д.1. Перший рівень складності.
Тягар D маси 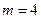 кг, одержавши в точці А початкову швидкість
кг, одержавши в точці А початкову швидкість 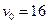 м/c, рухається по вигнутій трубі АВС, розташованій у вертикальній площині. Частини труби нахилені до горизонту під кутами
м/c, рухається по вигнутій трубі АВС, розташованій у вертикальній площині. Частини труби нахилені до горизонту під кутами 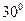 (частина АВ) і
(частина АВ) і 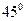 (частина ВС) (рис. 21.1). На ділянці АВ на тягар діють: сила ваги
(частина ВС) (рис. 21.1). На ділянці АВ на тягар діють: сила ваги 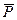 , задана постійна сила
, задана постійна сила 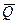 , величина якої
, величина якої 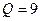 Н, і сила опору середовища
Н, і сила опору середовища 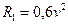 Н, напрямлена протилежно до руху тягаря. Довжина ділянки АВ
Н, напрямлена протилежно до руху тягаря. Довжина ділянки АВ 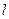 1 = 5 м.
1 = 5 м.
В точці В тягар, не змінюючи величини своєї швидкості, переходить на ділянку ВС. На цій ділянці на тягар діють: сила ваги 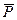 і змінна сила
і змінна сила 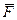 , проекція якої
, проекція якої 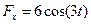 H.
H.
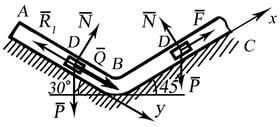
Рис. 21. 1.
Тягар вважати матеріальною точкою. Тертям ковзання на ділянках труби знехтувати.
Дано: 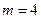 кг;
кг; 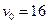 м/c;
м/c; 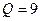 H;
H; 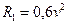 Н;
Н;
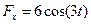 H;
H; 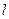 1= 5 м.
1= 5 м.
Визначити: закон руху тягаря на ділянці ВС, тобто 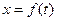 , де x = ВD.
, де x = ВD.
Розв’язання. 1. Розглянемо рух тягаря на ділянці АВ, вважаючи тягар матеріальною точкою. Покажемо на рис. 21.1 тягар в довільному положенні та прикладемо до нього всі діючі сили: 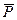 ,
, 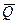 ,
, 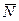 ,
, 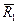 . Проводимо вісь Ау за напрямом руху тягаря і складаємо диференціальне рівняння:
. Проводимо вісь Ау за напрямом руху тягаря і складаємо диференціальне рівняння:
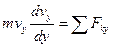 ; (1)
; (1)
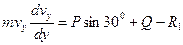 ; (2)
; (2)
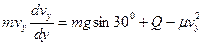 , (3)
, (3)
де 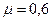 H
H  c2/м2.
c2/м2.
Поділимо обидві частини рівняння (3) на масу m:
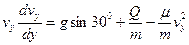 . (4)
. (4)
Позначимо:
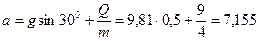 ;
; 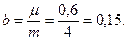
Тоді рівняння (4) приймає вигляд:
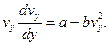 (5)
(5)
Розділимо змінні в рівнянні (5) і проінтегруємо:
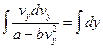 ;
;
оскільки 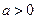 ,то
,то
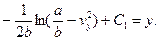 (6)
(6)
Визначимо сталу інтегрування 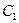 , враховуючи початкові умови: при
, враховуючи початкові умови: при 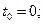
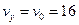 м/c;
м/c; 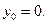
Тоді
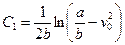 .
.
Одержимо
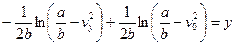 ;
;
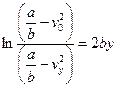 ;
;
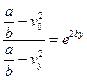 ;
; 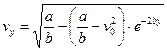 . (7)
. (7)
В момент, коли тягар попадає в точку В, 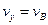 ;
; 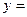
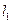 і
і 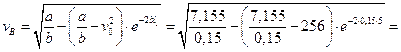
= 9,7 м/c.
Примітка 1. Якщо 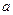 < 0, то з рівняння (5) знайдемо
< 0, то з рівняння (5) знайдемо
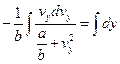 ;
;
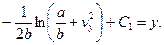
Враховуючи початкові умови 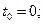
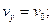
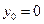 ,
,
одержимо
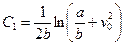 .
.
Тоді
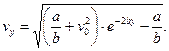
Примітка 2. Якщо сила опору середовища виражена формулою 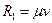 і заданий час руху t 1 по ділянці АВ, то диференціальне рівняння руху має вигляд
і заданий час руху t 1 по ділянці АВ, то диференціальне рівняння руху має вигляд
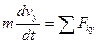 .
.
Далі потрібно спроектувати сили на вісь Аy, розділити змінні, проінтегрувати і знайти значення швидкості 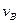 .
.
Наприклад, з даними задачі одержимо
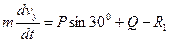 ;
;
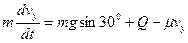 ;
;
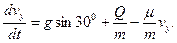
Позначимо:
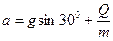 ;
; 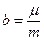 .
.
Тоді
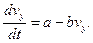
Розділимо змінні й проінтегруємо:
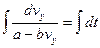 ;
;
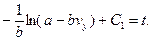
При 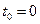 ;
; 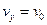 ;
; 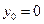 , тоді
, тоді 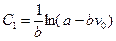 і
і
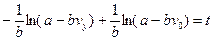 ;
;
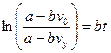 ;
;
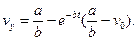
При 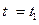 ;
; 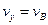 , тобто
, тобто
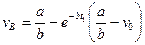 .
.
2. Тепер розглянемо рух тягаря на ділянці ВС. Знайдена швидкість 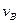 буде для руху по цій ділянці початковою швидкістю (
буде для руху по цій ділянці початковою швидкістю (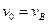 ).
).
Покажемо тягар в довільному положенні та прикладемо до нього всі діючі сили: 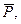
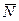 і
і 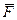 (рис. 21.1). Проведемо вісь Вx за напрямом руху тягаря і складемо диференціальне рівняння руху тягаря в проекції на цю вісь:
(рис. 21.1). Проведемо вісь Вx за напрямом руху тягаря і складемо диференціальне рівняння руху тягаря в проекції на цю вісь:
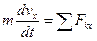 ; (8)
; (8)
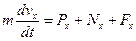 ;
;
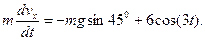 (9)
(9)
Поділимо обидві частини рівняння (9) на масу 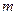 :
:
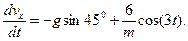 (10)
(10)
Розділимо змінні в рівнянні (10) і проінтегруємо:
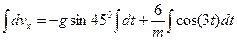 ;
;
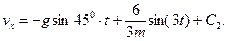 (11)
(11)
Врахуємо, що 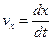 , тоді
, тоді
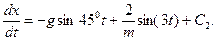 (12)
(12)
Розділимо змінні й знову проінтегруємо:
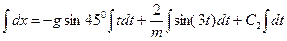 ; (13)
; (13)
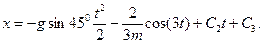 (14)
(14)
Для визначення сталих інтегрування С 2 і С 3 використаємо початкові умови: 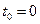 ;
; 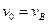 ;
; 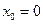 . Тоді, підставляючи початкові умови в рівняння (11) і (14), одержимо
. Тоді, підставляючи початкові умови в рівняння (11) і (14), одержимо
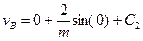 ;
; 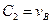 ; (15)
; (15)
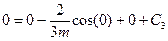 ;
; 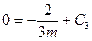 ;
;
 (16)
(16)
Рівняння руху тягаря на ділянці ВС приймає вигляд
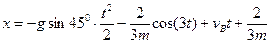 ;
;
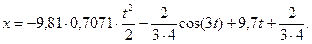
Остаточно 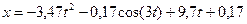 , м.
, м.
Відповідь: 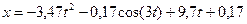 , м.
, м.






