3) 
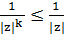
4) Нақты (1)-(3) аламыз. 
|| 
Онай қарасақ
5) 
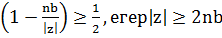
Сосын, бар
6) 
1/n
Нақты (4)-(6) анықтасақ
| 
1/2
Полинама модулінің үзіліссіздігі.
f-полинамасы z-тен кешенді сандардың өрісіне дейін. Көрініс көптікте анықталған С барлық кешенді сандар кешенді фуннкцияалардың ауыстырымдары бар. Біз оны полином моделі дейміз fжәне символмен белгіленеді. |f|
Теорема.1,2 f-C[z]-ғы кез-келген полином болсын полиномның модулі С жиынында үзіліссіз функция болады.
Дәлелдеуі:Көрсетсек, кейбір оң сандар Е табылады осындай оң 
кейбір кешенді сандар z,егер |z-a|< онда ||f(z)-|f(a)|<E
Теорема 1,3 анық,дұрыс егер полином f нөльдік және нөльдік дәрежесі болады.Полиномда f оң дәрежесі n бар
Жатқызсақ f дәрежесімен айырымы z-a:
f(z)=c0+c1(z-a)+…+cn(z-a)n (cn 
0)
Қаншалықты f(a)=c0 онда f(a)=c0, то
f(z)-f(a=c1(z-a)+…+cn(z-a)n
Және 4,7,8 теорема бойынша тең емес екендігін аламыз.
1. |f(z)-f(a)|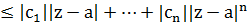 
Қойамыз: b=max {|c1|,…,|cn|}
Осымен Cn 
2. |z-a|k 
Байланысты (1) және (2) бар
|f(z)-f(a)| 
Осыған қарай, кез келген E>0
nb|z-a|<E |z-a|<E/nb
Әр сандарда Е сәйкесінше оң сандарды қойсақ
Сосын, кезкелген Е>0, кейбір z-тен С-ға 
Теорема:f-C[z] –ғы полимон болсын Егер <Zn> тізбекшесі а кешен санына сәйкес келсеб онда <|f(Zn)|> тізбекшесі |f(a)|-ға сәйкес келеді.
Дәлелдеуі: Теорема 1,2
1. (
Шарт бойынша, біртіндеп<Zn>жинақталатын санға а сосын кез келген 
n0 натуралды сандар бар|zn-a|<δ кейбір n>n0-ға
Осыдан (1) ары қарай 
Осы бейнеден, біртіндеп <|f(Zn)|> жинақталған санға |f(a|)
Полином моделінің ең кіші мәні:
Төмен қарай атақты анализдіңБольцано-Вейрштрасса тоеремасы керек: кей ақырсыз біртіндеп<Zn> нүктелі дөңгелек|z|≤r r-(фиксированды оң нақты сан) қолданады келесімі, кейбір жинақты нүктелік дөңглекте
Теорема 1,4, f-C[x] полином болсын r –оң нақты сан және m=inf|f(z)| онда |f(a)|=m және |a|≤r болатындай а кешен саны бар.
Дәлелдеуі:<En>біртіндеп оң нақты сан жинақты ноьлге
Осымен m=inf |f(z)| онда әрбір мүше En біртіндеп Zn, ,бар болуы
m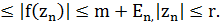 
Сондықтан біртінде <|f(zn)|> жинақталады m-ге:
(1) Барлық элемент біртіндеп<zn> дөңгелекте орналасқан |z| 
Б-В теорема бойынша, бұл біртіндеп келесіге жалғасады <Xn> жинақталған кейбір нүктелі а дөңгелегі |z|≤r
Теорема бойынша 1,3 3-ден келесі
Осымен |f(
келесіден келесіге біртіндеп|a(
жинақталады m-ге онда,
Негізінен (3), (4) және (5) аяақтаймыз |f(a)|=m және |a|≤r
Теорема 1,5 Кез келген полином модулі f осы C(z) өзінің ең кіші мәніне көктікте С жетеді
Дәлелдеуі Теорема, анығында дұрыс, егер deg f=0 немесе f(0)=0 Сондықтан ойлансақ degf≥1 және f(0)≠0 Осыдан M=|f(0)| Теорема 1,1 бойынша.
Болса 
Анықталады а саны осылай. 
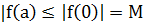
|f(a)|≤|f(z) егер |z|≤r
(2) Және (4) бар (
осы бейнеден |f| C ең кіші мәні нүктелі а жетеді.
Даламбера леммасы. Дәлелдеуі теорема 1,7 мәнді өлшемді негізінде келесі леммада, ол Даламбер леммасы дейміз.
Лемма 1,6 кешен сандар өрісінде берілген оң дәрежелі полимон Егер f(a)≠0 болса, |f(c)|<|f(a)| болатындай С кеншен саны бар.
Дәлелдеуі. F(x)=a0+…+anxn көпмүшелік дәрежесі n>0 және f(a) 
Қарастырсақ f дәрежелі айырымы бойынша х-а:
1) 
nқайда с1 
Қарастырсақ z=x-a және 
Cm-нөльдік емес коэффициент полиномы g ең кіші оң индексімен (0<m≤n) онда
Анықтасақ h(z)
H(z)= 
0 егер m=n
Онда теңдік былай жазуға болады 
(1) 
кез келген түбірді d-арқылы белгілейміз m дәрежелі саннан (-c0/cm)
Dm=-c0/cm.
Қарастырсақ (5) Z мәнінде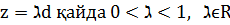 
(5) және (6) теңсіздігін аламыз
Негізінде (4) аяақтаймыз: 
- 
1
Осыдан аламыз.
9) 
-1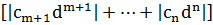 
егер m<n
B={
0. Егер m=n.
Белгімен енді n<nB>0, қаншалықты Сn және d нөлдіктен өзгеше, осыдан (8) және (9) теңсіздік шығады
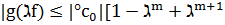B].
0<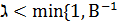 
}
|f(a+ 
{ енді m<n,
0< 
.
Виета формуласы:Түбірлер арасындағы арасындағы тәуелсіздікті анықтаймыз және полином коэффиценттің.
Теорема 1,11 (Виета) 
c1=-(a1+a2+…+an);
c2=a1a2+a1a2+a1a3+…+an-1zn;
c3=-(a1a2a3+…+an-2an-1an);
…………………………..
Cn=(-1)na1a2…an
Дәуелдеуі. Осымен а1,,,аn- полином түбірі f, ондакелесі 1,9 бойынша
Zn+c1+zn-1+…+cn-1z+cn=(z-a1)(z-a2)…(z-an)
Көбейтсек сызықтық көптікте оң жақ теңссіздікпен, онда аламыз келесі теңдеуді.
zn+c1zn-1+…+cn-1z+cn=zn-(a1+…+an)zn-1+…+(-1)na1a2…an.
осы теңсіздіктен екілік полином z-тен келесі теңсіздік коффиценті жалғыз дәрежелі z;теңдік коэффиценті жалғыз дәрежелі z, осыдан формула аламыз (1)
формулалар (1) Виета формуласы деп атлады.
Салдар1,12 егер a1…an- полином түбірі с0zn+c1zn-1+…+cn-1+cn дәрежелі n С[z]-тен,
Онда;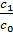 
=-(a1+…+an);
=a1a2+a1a3+…+an-1an
……………………….
na1a2…an.
