МОДЕЛИРОВАНИЕ
ЭЛЕКТРОМАГНИТНЫХ ПЕРЕХОДНЫХ
ПРОЦЕССОВ НА ЭВМ
Омск 2006
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Омский государственный технический университет»
МОДЕЛИРОВАНИЕ
ЭЛЕКТРОМАГНИТНЫХ ПЕРЕХОДНЫХ
ПРОЦЕССОВ НА ЭВМ
Методические указания
К лабораторным работам
Омск – 2006
.
Cоставители: Шкаруба Михаил Васильевич,
Эрнст Александр Дмитриевич
ЛАБОРАТОРНАЯ РАБОТА №1
МОДЕЛИРОВАНИЕ НА ЭВМ ХОЛОСТОГО ХОДА
ТРАНСФОРМАТОРА
Цель работы: Исследовать переходный процесс, возникающий при включении
однофазного трансформатора с разомкнутой вторичной обмот-
кой под синусоидальное напряжение.
Пояснения к работе.
Рассматриваемый процесс включения однофазного трансформатора с разомкнутой первичной обмоткой (рис.1.1) полностью идентичен процессу включения катушки с ферромагнитным сердечником под синусоидальное напряжение и описывается уравнением [1]

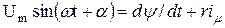 , (1.1)
, (1.1)
где Um - амплитуда синусоидального напряжения; a - фаза напряжения при t=0 (фаза включения);  - потокосцепление первичной обмотки; n1 - число витков первичной обмотки; Ф – магнитный поток;
- потокосцепление первичной обмотки; n1 - число витков первичной обмотки; Ф – магнитный поток;  - мгновенное значение тока холостого хода; r - активное сопротивление первичной обмотки.
- мгновенное значение тока холостого хода; r - активное сопротивление первичной обмотки.
Предполагается, что магнитная характеристика трансформатора (характеристика холостого хода) 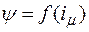 известна (рис. 1.2). Так как магнитная характеристика нелинейна, то и дифференциальное уравнение (1.1) будет нелинейным.
известна (рис. 1.2). Так как магнитная характеристика нелинейна, то и дифференциальное уравнение (1.1) будет нелинейным.
Решить это дифференциальное уравнение можно, например, методом условной линеаризации [1], который заключается в следующем. Пусть второе слагаемое в первой части уравнения (1.1) мало по сравнению с первым. Такое условие соблюдается, например, при включении мощных трансформаторов с разомкнутой вторичной обмоткой, так как активное сопротивление r у них обычно незначительно. Поэтому второе слагаемое  имеет второстепенное значение по сравнению с членом
имеет второстепенное значение по сравнению с членом  и неточность его вычисления существенно не повлияет на определение параметров переходного процесса.
и неточность его вычисления существенно не повлияет на определение параметров переходного процесса.
Зависимость  является нелинейной, так как L есть функция
является нелинейной, так как L есть функция  , но в данном случае можно приближенно принять L=const, и связь между
, но в данном случае можно приближенно принять L=const, и связь между  и
и 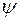 становится линейной:
становится линейной:
 (1.2)
(1.2)
 |
Рис.1.1– Исследуемая схема включения однофазного трансформатора
 |
Рис.1.2 – Магнитная характеристика трансформатора
 |
Рис. 1.3 – Кривая 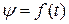 и ее составляющие:
и ее составляющие:
1 – апериодическая 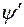 ; 2 – периодическая
; 2 – периодическая 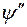
Отсюда можно выразить  и подставить в уравнение (1.1). Тогда уравнение (1.1) примет вид
и подставить в уравнение (1.1). Тогда уравнение (1.1) примет вид
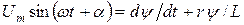 . (1.3)
. (1.3)
Уравнение (1.3) становится линейным и имеет решение
 (1.4)
(1.4)
где  - амплитуда потокосцепления; (a – j) – фаза включения потокосцепления; угол
- амплитуда потокосцепления; (a – j) – фаза включения потокосцепления; угол  .
.
Так как r<<( ), угол
), угол 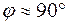 . Максимум потокосцепления соответствует фазе включения напряжения
. Максимум потокосцепления соответствует фазе включения напряжения  и определяется уравнением
и определяется уравнением
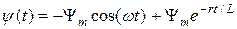 , (1.5)
, (1.5)
так как в этом случае  . На рис. 1.3 приведена зависи–мость
. На рис. 1.3 приведена зависи–мость 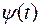 и ее составляющие –
и ее составляющие – 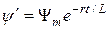 и
и  . Макси-мальное мгновенное значение потокосцепления
. Макси-мальное мгновенное значение потокосцепления 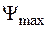 имеет место через поло–вину периода и при f =50 Гц можно записать
имеет место через поло–вину периода и при f =50 Гц можно записать
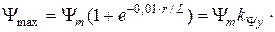 (1.6)
(1.6)
Из выражения (1.6) следует, что при большой постоянной времени  максимальное значение потокосцепления равно примерно
максимальное значение потокосцепления равно примерно  , а ударный коэффициент [2]
, а ударный коэффициент [2]  .
.
На рис. 1.2 приведена магнитная характеристика трансформатора. В установившемся режиме работы трансформатора амплитудное значение потокосцепления  находится вблизи колена магнитной характеристики. Этому значению потокосцепления соответствует наибольшая по величине амплитуда тока
находится вблизи колена магнитной характеристики. Этому значению потокосцепления соответствует наибольшая по величине амплитуда тока  , но при включении трансформатора амплитуда потокосцепления превышает
, но при включении трансформатора амплитуда потокосцепления превышает  (рис. 1.3), рабочая точка переходит в область насыщения кривой намагничивания, что приводит к очень большим броскам тока намагничивания.
(рис. 1.3), рабочая точка переходит в область насыщения кривой намагничивания, что приводит к очень большим броскам тока намагничивания.
На рис. 1.4 показана форма тока, соответствующая зависимости 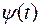 и построенная по кривой намагничивания. Видно (рис 1.4), что зависимость
и построенная по кривой намагничивания. Видно (рис 1.4), что зависимость 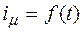 сильно отличается от синусоиды, особенно в начальной стадии переходного процесса. Это происходит потому, что при насыщении сердечника индуктивность становится нелинейной и вызывает возникновение нелинейного тока. Нелинейный ток можно разложить на высшие гармоники. (В курсе ”Электромагнитные переходные про-цессы” разложение тока на высшие гармоники не рассматривается. Однако в последние годы в электроэнергетике стали уделять большое внимание вопросам качества электроэнергии и студенты должны знать, что индуктивное сопротивление трансформатора при насыщении становится нелинейным, а нелинейное сопротивление можно рассматривать как генератор высших гармоник [1], ко-торое приводят к искажению синусоидальной формы тока и напряжения и, следовательно, ухудшение качества электроэнергии. Данная лабораторная работа очень удобна для знакомства с этим вопросом, полученные сведения будут использованы в курсах ”Электроснабжение промышленных предприятий”, ”Изоляция и перенапряжения в СЭС” и других).
сильно отличается от синусоиды, особенно в начальной стадии переходного процесса. Это происходит потому, что при насыщении сердечника индуктивность становится нелинейной и вызывает возникновение нелинейного тока. Нелинейный ток можно разложить на высшие гармоники. (В курсе ”Электромагнитные переходные про-цессы” разложение тока на высшие гармоники не рассматривается. Однако в последние годы в электроэнергетике стали уделять большое внимание вопросам качества электроэнергии и студенты должны знать, что индуктивное сопротивление трансформатора при насыщении становится нелинейным, а нелинейное сопротивление можно рассматривать как генератор высших гармоник [1], ко-торое приводят к искажению синусоидальной формы тока и напряжения и, следовательно, ухудшение качества электроэнергии. Данная лабораторная работа очень удобна для знакомства с этим вопросом, полученные сведения будут использованы в курсах ”Электроснабжение промышленных предприятий”, ”Изоляция и перенапряжения в СЭС” и других).
Разложим ток  на высшие гармоники. Из курса математики известно, что любую периодическую функцию y=f(x), удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье, а, как известно, все периодические функции электротехники условиям Дирихле удовлетворяют [1]. В общем виде разложение функции y=f(x) в ряд Фурье можно представить так [1]:
на высшие гармоники. Из курса математики известно, что любую периодическую функцию y=f(x), удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье, а, как известно, все периодические функции электротехники условиям Дирихле удовлетворяют [1]. В общем виде разложение функции y=f(x) в ряд Фурье можно представить так [1]:

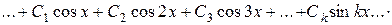 (1.7)
(1.7)
Здесь  - постоянная составляющая;
- постоянная составляющая;  -амплитуда основной (первой) синусной гармоники;
-амплитуда основной (первой) синусной гармоники;  -амплитуда высшей (k-й) синусной гармоники;
-амплитуда высшей (k-й) синусной гармоники;  - амплитуда основной (первой) косинусной гармоники;
- амплитуда основной (первой) косинусной гармоники; 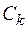 - амплитуда высшей (k-й) косинусной гармоники.
- амплитуда высшей (k-й) косинусной гармоники.
Если периодические кривые обладают симметрией того или иного вида, то некоторые коэффициенты в разложении в ряд Фурье (1.7) обращаются в нуль [1]. Так, если кривая симметрична относительно оси ординат,то в разложении в ряд Фурье отсутствуют следующие коэффициенты: 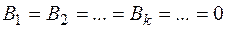 - и оно принимает вид:
- и оно принимает вид:
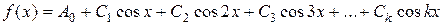 (1.8)
(1.8)
Амплитуды постоянной составляющей  и гармоник
и гармоник 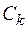 определяются по формулам [1]
определяются по формулам [1]
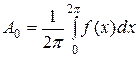 и
и  (9.1)
(9.1)
 Коэффициенты ряда Фурье по известной кривой y=f(x) можно определить графическим методом [1], основанным на замене определенных интегралов (1.9) суммами конечного числа слагаемых. С этой целью период функции f(x), равный
Коэффициенты ряда Фурье по известной кривой y=f(x) можно определить графическим методом [1], основанным на замене определенных интегралов (1.9) суммами конечного числа слагаемых. С этой целью период функции f(x), равный  , разбивается на n равных частей
, разбивается на n равных частей  и интегралы заменяются суммами:
и интегралы заменяются суммами:

и
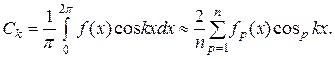 (1.10)
(1.10)
Здесь p - текущий индекс, он принимает значение 1….n;  - значение функции f(x) в середине p-го интервала;
- значение функции f(x) в середине p-го интервала; 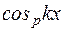 - значение функции
- значение функции  в середине p-го интервала.
в середине p-го интервала.
Однако ток холостого хода трансформатора 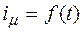 во время переходного процесса в общем случае периодической функцией не является, поэтому, строго говоря, его разложить на гармоники нельзя. Вместе с тем, рассматривая переходный процесс за один период можно считать функцию квазипериодической. Это после разложения кривой тока на высшие гармоники позволяет определить действующее значение тока и тепловой импульс за первый период [3]. Иное дело – ток в цепи при r=0. В этом случае функция
во время переходного процесса в общем случае периодической функцией не является, поэтому, строго говоря, его разложить на гармоники нельзя. Вместе с тем, рассматривая переходный процесс за один период можно считать функцию квазипериодической. Это после разложения кривой тока на высшие гармоники позволяет определить действующее значение тока и тепловой импульс за первый период [3]. Иное дело – ток в цепи при r=0. В этом случае функция 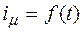 будет периодической и симметричной относительно оси ординат (рис 1.5).
будет периодической и симметричной относительно оси ординат (рис 1.5).
Ряд Фурье для тока намагничивания 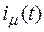 при r=0 принимает вид:
при r=0 принимает вид:
 (1.11)
(1.11)
где  -постоянная составляющая;
-постоянная составляющая; 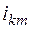 -амплитуда k-й косинусной гармоники
-амплитуда k-й косинусной гармоники
В лабораторной работе при определении постоянной составляющей  и амплитуд косинусных гармоник
и амплитуд косинусных гармоник 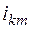 период разбивается на 48 частей, и они определяются по формулам:
период разбивается на 48 частей, и они определяются по формулам:

 (1.12)
(1.12)
где 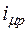 - значения тока
- значения тока  в середине р-го интервала;
в середине р-го интервала;
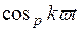 - значение функции
- значение функции  в середине р-го интервала.
в середине р-го интервала.
Число гармоник в лабораторной работе выбирается так, чтобы по-грешность вычисления амплитуды тока  не превышала 5%, поэтому она зависит от исходных данных и изменяется от 5 до 7. На рис. 1.6 приведено разложение тока намагничивания
не превышала 5%, поэтому она зависит от исходных данных и изменяется от 5 до 7. На рис. 1.6 приведено разложение тока намагничивания 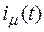 на гармоники при r=0.
на гармоники при r=0.
Наибольшее значение тока намагничивания 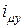 – бросок намагничивающего тока возникает через полупериод (0,01 с). Величина
– бросок намагничивающего тока возникает через полупериод (0,01 с). Величина 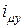 может в десятки раз превосходить амплитуду тока установившегося режима
может в десятки раз превосходить амплитуду тока установившегося режима  . Следовательно, в нелинейных цепях ударный коэффициент может значительно превосходить максимальное значение
. Следовательно, в нелинейных цепях ударный коэффициент может значительно превосходить максимальное значение  в линейных цепях не превышающее значения
в линейных цепях не превышающее значения 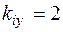 . Такой всплеск тока может вызвать механические разрушения обмотки, так как электродинамические усилия пропорциональны квадрату тока.
. Такой всплеск тока может вызвать механические разрушения обмотки, так как электродинамические усилия пропорциональны квадрату тока.
 |
|
 и построенная по кривой
и построенная по кривой
намагничивания
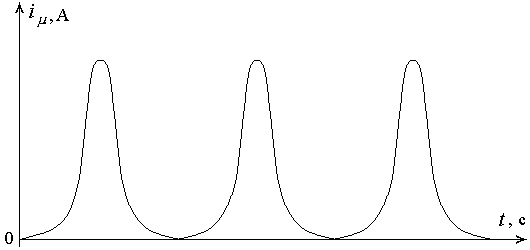 |
Рис. 1.5 – Кривая тока
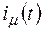 для r=0
для r=0
Оценка бросков намагничивающего тока 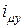 важна и для правильной работы защиты трансформатора, которая не должна срабатывать при его включении. Для этого можно мощный ненагруженный трансформатор включить через дополнительное сопротивление
важна и для правильной работы защиты трансформатора, которая не должна срабатывать при его включении. Для этого можно мощный ненагруженный трансформатор включить через дополнительное сопротивление  , которое затем необходимо замкнуть накоротко (рис. 1.1)
, которое затем необходимо замкнуть накоротко (рис. 1.1)
В лабораторной работе зависимость y(t) строится по уравнению (1.5), а зависимость 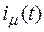 – по рис. 1.4 [2]. Поэтому необходимо ввести в ЭВМ магнитную характеристику трансформатора, лежащую в I и III квадрантах. Так как кривая намагничивания симметрична, то достаточно определить характеристику в I квадранте. В численных расчетах нелинейную зависимость
– по рис. 1.4 [2]. Поэтому необходимо ввести в ЭВМ магнитную характеристику трансформатора, лежащую в I и III квадрантах. Так как кривая намагничивания симметрична, то достаточно определить характеристику в I квадранте. В численных расчетах нелинейную зависимость  обычно аппроксимируют несколькими линейными участками. В лабораторной работе не требуется высокой точности расчетов, поэтому магнитную характеристику одного квадранта достаточно заменить пятью линейными участками (рис. 1.7).
обычно аппроксимируют несколькими линейными участками. В лабораторной работе не требуется высокой точности расчетов, поэтому магнитную характеристику одного квадранта достаточно заменить пятью линейными участками (рис. 1.7).
В табл. 1.1 приведены номинальные напряжения силовых трансформаторов и координаты точек излома линейных участков магнитных характеристик для различных сортов стали [4]. Сердечник трансформатора выбран так, чтобы при максимальном напряжении, приложенном к нему, 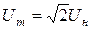 , ток был практически синусоидальным. Однако во время переходного процесса напряжение превышает
, ток был практически синусоидальным. Однако во время переходного процесса напряжение превышает 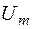 , ток начинает отличаться от синусоиды и появляются высшие гармоники.
, ток начинает отличаться от синусоиды и появляются высшие гармоники.
Среднее значение индуктивности L обмотки с сердечником определялось в точке 3 кривой намагничивания (рис 1.7) и приведено в табл. 1.2.

Рис. 6.1– Разложение тока  на гармоники
на гармоники
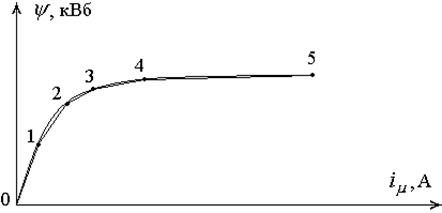 |
Рис. 7.1– Построение кривой намагничивания в I квадранте.
Описание схемы алгоритма программы
Программа написана на языке модульного программирования Borland
Delphi 7 и работает в режиме диалога. Программа (блок–схем приведена на рис. 1.8) начинается с вывода на экран монитора названия лабораторной работы, исследуемой схемы и целей работы. Для запуска программы необходимо ввести исходные данные: номер варианта, номинальное напряжение трансформатора, индуктивность цепи и координаты точек излома аппроксимированной кривой намагничивания сердечника.
Введенные координаты точек излома аппроксимированной кривой намагни-чивания появляются на экране в виде таблицы. Если при вводе допущены ошибки, то его нужно повторить.
После очистки экрана на нем появляется кривая намагничивания сердечника трансформатора  аппроксимированная пятью линейными участками. Она изображена в I и III квадрантах.
аппроксимированная пятью линейными участками. Она изображена в I и III квадрантах.
Лабораторная работа разбита на два этапа. На первом этапе сначала изучается работа трансформатора под нагрузкой на линейной части кривой намагничивания (рис.1.7). На экран последовательно выводятся кривые  ,
, 
 , все эти зависимости близки к синусоидам.
, все эти зависимости близки к синусоидам. 
Затем исследуется процесс включения трансформатора с разомкнутой вторичной обмоткой и сопротивлением первичной обмотки r=0. Сначала на экране появляется зависимость  и ее периодическая и апериодическая составляющие, по ней вычисляются максимальное значение
и ее периодическая и апериодическая составляющие, по ней вычисляются максимальное значение 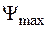 и коэффициент
и коэффициент  . Следом за графиком выводится таблица для его построения.
. Следом за графиком выводится таблица для его построения.

Рис. 1.8– Укрупненная блок–схема алгоритма программы
После смены окна начинается построение кривой  =
= 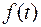 . Порядок по-строения этой зависимости следующий: сначала вычисляется зависимость
. Порядок по-строения этой зависимости следующий: сначала вычисляется зависимость  , и для каждого значения потокосцепления
, и для каждого значения потокосцепления 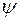 по кривой намагничивания определяется соответствующее значение тока, которое выводится на экран в виде точки. Одновременно с построением зависимости
по кривой намагничивания определяется соответствующее значение тока, которое выводится на экран в виде точки. Одновременно с построением зависимости  =
= 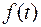 идет определение максимального значения тока
идет определение максимального значения тока 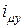 и ударного коэффициента
и ударного коэффициента  , которые после окончания построения выводятся на экран.
, которые после окончания построения выводятся на экран.
Кривая тока 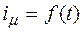 для r=0 раскладывается на гармоники. Сначала на экран выводится число гармоник, амплитуды гармоник и погрешность расчета, а потом появляется само разложение тока на гармоники. В отчете этот график из-за сложности можно не приводить. Следом разложение повторяется еще раз. Только теперь, чтобы гармоники не сливались, на экран выводится только один период тока
для r=0 раскладывается на гармоники. Сначала на экран выводится число гармоник, амплитуды гармоник и погрешность расчета, а потом появляется само разложение тока на гармоники. В отчете этот график из-за сложности можно не приводить. Следом разложение повторяется еще раз. Только теперь, чтобы гармоники не сливались, на экран выводится только один период тока  (рис. 1.6), а гармоники строятся поочередно. Затем выводятся таблицы для построения гармоник в отчете.
(рис. 1.6), а гармоники строятся поочередно. Затем выводятся таблицы для построения гармоник в отчете.
Этап заканчивается контролем правильности его выполнения. Для этого с клавиатуры необходимо ввести значения основных параметров, полученных в результате расчета. Если эти значения совпадут с контрольными ответами, то на экране появляется сообщение о том, что этап выполнен верно. Если в работе будут допущены хотя бы небольшие неточности, то на экране появится сообщение, что этап выполнен не верно и сколько допущено ошибок. Этап придется повторить заново.
На втором этапе работы исследуется влияние сопротивление цепи r на максимальные значения потокосцепления и тока. На этом этапе необходимо построить зависимости  ,
,  для четырех значений сопротивления r, приведенных в табл. 1,2. Во время построения зависимостей
для четырех значений сопротивления r, приведенных в табл. 1,2. Во время построения зависимостей  ,
,  вычисляются значения
вычисляются значения 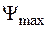 ,
,  ,
,  ,
,  и записываются в табл. 1.3. Для r3 зависимости
и записываются в табл. 1.3. Для r3 зависимости  ,
,  нужны для отчета, поэтому на экран также выводятся таблицы для их построения. С увеличением сопротивления r резко уменьшается амплитуда тока намагничивания, и зависимость
нужны для отчета, поэтому на экран также выводятся таблицы для их построения. С увеличением сопротивления r резко уменьшается амплитуда тока намагничивания, и зависимость  может занимать малую часть экрана. В этом случае в программе предусмотрены вычисления нового масштаба по току таким образом, чтобы при повторном построении зависимость
может занимать малую часть экрана. В этом случае в программе предусмотрены вычисления нового масштаба по току таким образом, чтобы при повторном построении зависимость 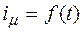 занимала почти весь экран. Второй этап также заканчивается контролем правильности его выполнения. Для этого с клавиатуры необходимо ввести значения коэффициентов
занимала почти весь экран. Второй этап также заканчивается контролем правильности его выполнения. Для этого с клавиатуры необходимо ввести значения коэффициентов 
 для всех четырех значений r. По ним строятся зависимости
для всех четырех значений r. По ним строятся зависимости 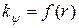 и
и  и они будут сравниваться с контрольными ответами. Если будут найдены отличия, то появится сообще-ние о количестве ошибок.
и они будут сравниваться с контрольными ответами. Если будут найдены отличия, то появится сообще-ние о количестве ошибок.
В конце работы появляется сообщения о правильности выполнения всей работы, и на каком этапе допущены ошибки. По этому сообщению преподаватель в конце работы может сделать вывод о всей работе. Контроль позволяет студентам, имеющим свои компьютеры, а также студентам, пропускающим занятия, выполнять лабораторные работы самостоятельно без преподавателя и оценивать правильность их выполнения.





 для R=0
для R=0

