В некоторых случаях на колебательную систему действует внешняя периодическая сила, которая заставляет систему совершать вынужденные колебания. Но колебательная система имеет и свою собственную частоту колебаний, которая определяется параметрами системы. Когда частота вынужденных колебаний совпадёт с частотой собственных колебаний, произойдёт резонанс.
Резонанс – это резкое увеличение амплитуды колебаний системы при совпадении частоты вынужденных колебаний с частотой собственных колебаний.
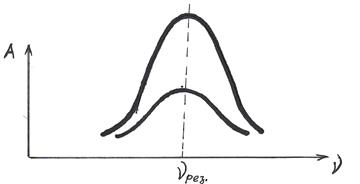
График зависимости амплитуды колебаний системы от частоты вынужденных колебаний называется резонансной кривой.
Форма резонансной кривой зависит от добротности колебательной системы. Чем меньше в системе потерь на трение, тем выше добротность и тем круче и острее идёт резонансная кривая
Там, где на практике используют резонанс, добротность колебательной системы стараются сделать высокой, т.е. уменьшить трение. Например, в механических часах, в измерительных приборах вибрационного типа, в качелях и т.д. В других случаях резонанс стараются подавить, там стараются добротность колебательной системы сделать как можно меньше. Например, в рычажных весах, в стрелочных измерительных приборах, при конструировании мостов, турбогенераторов и т.д.
Механические волны
А) Общая характеристика волны. Волны продольные и поперечные.
Волна – это процесс распространения колебаний в упругой среде. Для того, чтобы волна могла существовать, необходимы следующие условия. Во-первых, должно быть наличие материальных частиц, обладающих массой; во-вторых, должно быть наличие упругой связи между этими частицами.
Волны можно классифицировать по направлению колебаний частиц:
Поперечные
Продольные
По характеру колебаний частиц:
Бегущие
Стоячие
В поперечной волне частицы колеблются в поперечном направлении, по отношению к направлению распространения; поперечная волна может распространяться только в тех средах, в которой деформация сдвига вызывает упругую силу противодействия, т.е. только в твёрдых телах, а также на свободно висящем шнуре. Поперечная волна обладает свойством поляризации.
В продольной волне частицы колеблются в продольном направлении по отношению к направлению распространения. Эта волна может распространяться в тех средах, в которых деформация сжатия-растяжения вызывает упругую силу противодействия, т.е. и в твёрдых, и в жидких, и в газообразных телах.
В бегущей волне частицы колеблются так, что между двумя соседними частицами сушествует одинаковый сдвиг фаз. Иными словами, все частицы являются равноправными. Бегущая волна переносит энергию, но само вещество волной не переносится.
В стоячей волне все частицы колеблются синхронно, причём, частицы в пределах двух соседних полуволн колеблются в противофазе. Частицы же в пределе одной полуволны колеблются в одной фазе. Стоячая волна энергию не переносит, она её только перераспределяет в себе: в узлах энергия отсутствует, а в пучностях имеет максимум
Б) Уравнение волны
В уравнении волны две переменные: время t и координата x. Для наглядности рассмотрим поперечную волну. В ней все точки колеблются вдоль вертикальной оси S и колебания всех точек сдвинуты по фазе так, что если мы сделаем мгновенный фотоснимок волны, а через промежуток времени t сделаем ещё один снимок.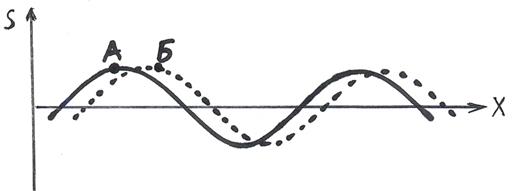 
Мы увидим, что за этот промежуток времени волна сместилась на некоторое расстояние. Причём, из чертежа видно, что точка Б отстаёт от точки А на некоторый угол f. Уравнение колебаний точки А:
S = Asinwt
Точки Б:
S = Asinw(t - t) t = X/u
Или:
S = Asinw(t – X/u)
Где u - скорость волны.
Таким образом, смещение S является функцией двух переменных: t и х,
Т.е. S = f(X, t)
График волны даёт моментальную фотографию волны.
В) Энергия волны
Мгновенное значение полной механической энергии одной частицы:
E = mA2w2
2
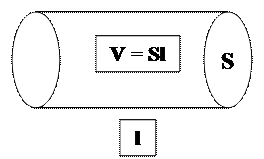
Выделим в среде некоторый объём V. В этом объёме находится N частиц, массой mo каждая. Общая энергия всех частиц:
E = NmoA2w2
2
Плотность среды:
r = m/V = Nmo/V
Тогда:
Nmo = rV
Общая энергия:
E = rVA2w2 = (rA2w2) V = eV
2 2
Здесь e - объёмная плотность энергии (Дж/м3)
А через площадку S за время t: и учитывая, что V = Sl
E = rVA2w2 = rSlA2w2 = rA2w2 = eu
St 2St 2St 2
E = I – интенсивность волны (Вт/м2) Тогда: I = eu
St
Это и есть уравнение Умова. Оно показывает, что интенсивность волны равна произведению объёмной плотности энергии волны на скорость её распространения.
