ЛЕКЦИЯ 1
Механические колебания и волны.
План лекции
Гармонические колебания
А) Общая характеристика и уравнение колебательного движения
Б) Баланс энергии при колебательном движении
В) Сложение гармонических колебаний
Г) Гармонический спектр простого и сложного колебания
Д) Затухающие колебания
Е) Вынужденные колебания. Резонанс.
Механические волны
А) Общая характеристика волны. Волны продольные и поперечные.
Б) Уравнение плоской волны
В) Поток энергии волны. Уравнение Умова.
Гармонические колебания
а) Общая характеристика и уравнение колебательного движения.
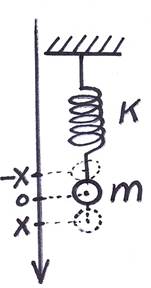
Колебательное движение – один из видов механического движения. В жизни оно встречается повсюду: маятник в настенных часах, груз, подвешенный на пружине, вода в открытом сосуде, вагон на рессорах, корабль на волнах и др. Главной характерной чертой колебательного движения является его повторяемость, т.е. каждое последующее движение повторяет предыдущее.
Для осуществления колебательного движения необходимы следующие условия: во-первых, должно быть наличие инертной массы, во-вторых, при выведении тела из положения равновесия должна возникать возвращающая сила. Данная сила должна быть пропорциональна величине отклонения тела от положения равновесия. Данная сила сообщает телу ускорение.
F = -kX - сила упругости; F = ma - сила инерции.
В данном случае, сила упругости является силой инерции: ma = -kX
Отсюда: a = -(k/m)X Введём обозначение: k/m = w2 Здесь w - циклическая частота колебаний. Перепишем это уравнение в виде:
d2X/dt2 = -w2X
Это – дифференциальное уравнение 2-го порядка. Представим его в виде:
d2X/dt2 + w2X = 0
где d2X/dt2 = kX/m w = k/m
Частное решение этого уравнения будет выглядеть так:
X = A sin (wt + fо)
Здесь:
X - текущая координата
A - амплитуда
w - циклическая частота
t - время
f - фаза
fо - начальная фаза.
Следует напомнить, что здесь, как и во всей физике принято координату и амплитуду измерять в метрах, время – в секундах, фазу – в радианах, циклическую частоту – в с-1.
Кроме того, в физике колебательного движения приняты следующие единицы:
n - частота (Гц)
Т - период (с)
Частота (в герцах) показывает, сколько колебаний совершит тело за 1 секунду.
Частота w (в с-1) показывает, сколько колебаний тело совершит за 2p секунд.
Период Т показывает продолжительность одного полного колебания (в секундах)
Особенность колебательного движения в том, что его легко можно связать с вращательным. Если представить себе какое-либо тело, движущееся по окружности в плоскости чертежа, то тень от него, падающая на вертикальную ось координат Х, будет совершать колебания вверх-вниз и если развернуть это движение на горизонтальную ось t, то получится кривая, являющаяся синусоидой.

Следует заметить, что графиком частного решения вышеуказанного дифференциального уравнения является кривая той же формы:

Наибольшее затруднение у студентов вызывает понятие фазы. В колебательном движении фаза играет туже роль, что координата в поступательном движении.
Сравним:
X = (ut + X) для поступательного движения
f = (wt + f) для колебательного движения
В колебательном движении фаза показывает, какая часть периода прошла от начала колебания.
Зная, что координата колеблющегося тела изменяется по закону:
Х = А sin (wt + f)
найдём закон, по которому изменяется скорость и ускорение:
u = X\ = A w cos(wt + f)
a = u \ = X\\ = -Aw2sin (wt + f)
Отсюда видно, что координата, скорость и ускорение изменяются либо по закону синуса, либо по закону косинуса. Причём, производная любого порядка даст либо синус, либо косинус. Из этого следует, что синус и косинус являются гармоническими функциями. Значит движение, осуществляющееся по законам синуса или косинуса является гармоническим колебанием, или колебанием, типа «проще некуда».
Все эти три графика представляют собой кривую одинаковой формы, только эти кривые сдвинуты относительно друг друга на 90о







