1. Дії з комплексними числами.
2. Вираження синусоїдних величин комплексними числами.
3. Закон Ома. Комплексні значення опорів та провідностей.
4. Визначення повної потужності за комплексами напруги і струму.
5. Розрахунок простих електричних кіл змінного струму символічним методом.
6. Розрахунок складних електричних кіл.
Дом. завд. [1] ст. 273-283 зад. 15.4 повторити стор. 71-92
1. Комплексним числом називають алгебраїчну суму матеріального і уявного чисел.
Геометричне комплексне число зображують у вигляді вектора в системі матеріальній та уявній осей. Комплексне число має три форми запису:
а) алгебраїчну А=А'+jА"; А=-А'+jА''';
б) тригонометричну А== |А|(соs α± jsin α)
в) показову А= |А| е±jα
де А - комплексне число; |А| модуль або
довжина вектора; е - основа натуральногологарифму; α - кут між матеріальною віссю та відрізком, який зображує комплексне число.
Відлік кута α ведуть від матеріальної вісі проти годинникової стрілки, виражають у радіанах tg α = A”/A’.
Сполучені комплекси - відрізняються один від одного знаком перед уявною частиною, наприклад 6+j8 та 6-j8, або 20(соs 37°+jsin37°) та 20(соs37°-jsin37°);
10е+j 30° та 10е-j 30°.
Геометрична величина j - поворотний множник на кут π/2 проти стрілки годинника.
Додавання та віднімання двох комплексних чисел виконують тільки у алгебраїчній формі:
А=(6+j8)+(4+j3)=(6+4)+ j(8+3)=10+11j; А=(6-j8)-(4-j3)=(6-4)+j(-8+3)=2-j5
Множення та ділення двох комплексних чисел можливо виконувати як у алгебраїчній, так і у показовій формах.
Нехай А1=12-j16; А2=4+j3; при множенні:
А=(12-j1б)(4+j3)=48-j64+j36+48=96-j28 при діленні
A=(12-j16)/(4-jЗ)= (12-j16)*(4-jЗ)/(4+j3)* (4-j3)= (48-j64-j36+j2 48)/(42+32)=-j100/25=-j4
Нехай А1=20е-j53°; А2=5ej37°
При множенні А=20е—j53°* 5еj37° =20 *5еj(-53°+37°)=100e-j16
При діленні А=20е-53°/5еj37° =(20/5) е -j(-53°+37°)=4e-j 90°
Зміна форми запису комплексного числа
1) Перетворення алгебраїчної форми у показникову
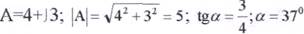А=5еj37°; ^А=|А|еjarctgα
2) Перетворення показникової форми у алгебраїчну A=10e-j37°
2. Синусоїдну функцію графічно можливо зобразити вектором, який обертається. Комплексне число також можливо зобразити вектором і визначити його модуль і фазу (аргумент - кут α), тобто будь яка синусоїдна функція може бути зображена комплексним числом.
При зображенні електричних величин комплексними числами усі формули, закони і методи розрахунків кіл постійного струму можливо застосувати для кіл змінного струму.
Напруга, виражена у комплексному вигляді, позначається великою літерою з крапкою над нею (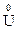
), а її модуль тією ж літерою без крапки (U). Модуль комплексної напруги є діючим значенням напруги.
Якщо напруга u=Umsin (ωt+ψ), то вектор цієї напруги має довжину U= Um/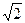 
, то кут нахилу вектора до осі абсцис ψ. Цей вектор можливо виразити комплексним числом з модулем, який дорівнює діючому значенню, а аргументом - начальній фазі:
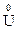=Uеjψ Якщо U = Umsin (ωt-ψ), то 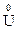= Uе-jψ
Якщо U= Umsin ωt,то 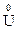=Uеj0 =U
Переводячи цей вираз у алгебраїчну форму, отримаємо 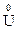=Uеjψ=U(соsφ+jsinφ)=Uсоsψ+jUsinψ, оскільки Uсоsψ =Uа, Usinψ=Up, то 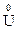=Uа+ jUp
тобто матеріальна частина комплексного числа - це активна складова напруги, а уявна частина - її реактивна складова. Знак плюс у реактивної складової значить індуктивний, а знак мінус - ємнісний характер кола.
Усі вирази, виведені для напруги, можливо віднести і до струму, де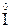 
- комплекс струму, І - модуль комплексу струму.
Фаза струму відносно напруги кола залежить від характера навантаження, тобто підключених до кача елементів.
Для rL - кола: u = Umsin ωt; і = Imsin (ωt-ψ); 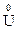= Uеj0 = U; 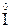= Іе-jφ або І = Іa-j Iр
Для rС кола: u = Umsin ωt; і = Imsin (ωt+ψ); 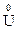= Uеj0 = U; = Іе-jφ =Іa+j Iр
