Измерение теплоемкости воздуха

 

Цель работы: Ознакомиться с понятием теплоемкости вещества, освоить технику измерения теплоемкости воздуха методом проточного калориметрирования.

 

Задание

1. Провести опыты по определению удельной изобарной теплоемкости воздуха при тепловом режиме, указанном преподавателем.

2. Рассчитать средние значения теплоемкостей C_pm и C_vm, изменения внутренней энергии 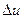, энтальпии и энтропии , а также показатель адиабаты воздуха k в условиях опыта.

3. Составить отчет о выполненной работе, который должен содержать: задание, основы теории (кратко), схему экспери-ментальной установки, таблицу опытных данных, обработку опытных данных и результаты опытов в виде таблицы.

Основы теории

 

При проведении расчетов процессов и аппаратов химической технологии часто приходится определять количество подведенной или отведенной теплоты. Наиболее просто это сделать, используя теплоемкость теплоносителей.

Удельной теплоемкостью называется количество теплоты, которое необходимо подвести к единице количества вещества, чтобы изменить его температуру на 1 градус. В связи с этим определением различают:

- удельную массовую теплоемкость

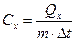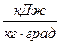, , откуда 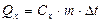, кДж; (1)

- удельную объемную теплоемкость

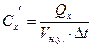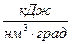, , откуда 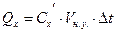, кДж; (2)

- удельную мольную теплоемкость

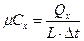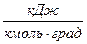, , откуда 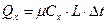, кДж, (3)

где m – масса газа, кг;

V_{н.у .}, нм³ – объем газа, приведенный к нормальным условиям (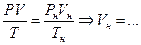, Р_н =760 мм рт. ст.=1,013×10⁵ Па, Т_н =273 К);

L – число киломолей вещества (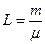), кмоль;

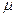- молекулярная масса газа, кг/кмоль;

_х – индекс, указывающий характер процесса подвода теплоты Q_x, например, при (Q_p), при 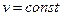(Q_v).

Поэтому различают:

С_р – изобарная теплоемкость,

С_v – изохорная теплоемкость.

Эти теплоемкости для идеальных газов связаны уравнением Майера:

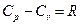. (4)

	С
		С=f(t)-нелинейная СХ=a+bt+et2+… а

t

Рис.1. Зависимость теплоемкости от температуры

б С=f(t)-линейная СХ=a+bt

СХ=const в

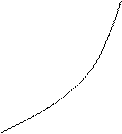
Теплоемкость зависит от температуры в общем случае нелинейно (рис. 1 а). При определении количества теплоты для нагревания при 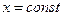от t₁ до t₂ обычно применяют средние теплоемкости 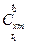(здесь индекс «m» означает «средний»!), которые при нелинейной зависимости рассчитываются по средним табличным значениям теплоемкостей 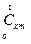в интервале температур от 0 до t:

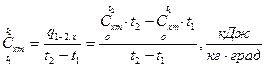, (5)

где 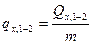- удельная массовая теплота, кДж/кг.

Следовательно

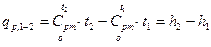, (6)

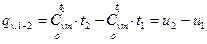, (7)

т.е. наиболее точно теплоту можно подсчитать как по значениям теплоемкостей, так и по значениям энтальпий h (при ) и внутренних энергий u (при 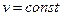). Значения 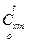, u и h приводятся в справочной литературе в виде таблиц /2/.

В пределе при уменьшении интервала температур в выражении (5) получим теплоемкость при заданной температуре t, называемую истинной теплоемкостью, С_х,ист.

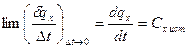. (8)

Со средней теплоемкостью она связана соотношением

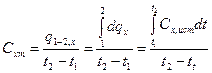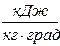, . (9)

Для приближенных расчетов можно учесть линейную зависимость теплоемкости от температуры (рис. 1б):

 

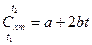, (10)

где a и b – индивидуальные коэффициенты (из таблиц /2/), .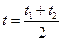

В соответствии с молекулярно-кинетической теорией внутренняя энергия газов распределяется равномерно по степеням свободы i поступательного и вращательного движения молекул. Для одноатомной молекулы i = 3 степеням свободы поступательного движения, т.е. изменяется положение молекулы в координатах x, y и z. Для двухатомных молекул к трем степеням свободы поступательного движения добавляются две степени свободы вращательного движения i = 3+2 = 5. С некоторой корректировкой для трех- и многоатомных газов число степеней свободы принимается равным i = 7.

Для идеальных газов при не очень высоких температурах на каждую степень свободы при 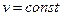расходуется энергия 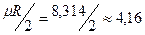кДж/(кмоль×град). Поэтому постоянные (рис.1, в) мольные теплоемкости можно определить по числам степеней свободы i, а 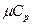- по (i + 2) из таблицы 1.

Таблица 1

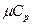Атомность газов	, кДж/(кмоль×град)	, кДж/(кмоль×град)
1 атомные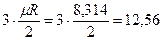
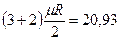
2 атомные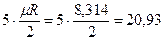
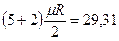
3 и многоатомные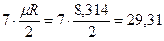

 

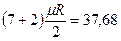
Для пересчета различных удельных теплоемкостей удобны соотношения:

, ; , ;

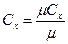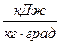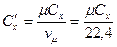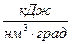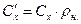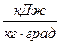, , (11)

где 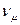- удельный объем 1 кмоля газа при нормальных условиях, .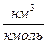