По приведенным ниже данным:
а) построить групповую таблицу, показывающую зависимость между двумя признаками;
б) дать графическое изображение зависимости;
в) рассчитать линейный коэффициент корреляции;
г) оценить существенность коэффициента корреляции;
д) сделать выводы.
Задача 51 - Имеются следующие данные о ширине ковшей пескомоек и их производительности:
Таблица 30
| Номер пескомойки | Ширина ковшей, мм | Средняя часовая производительность, м3 |
| 5,5 | ||
| 7,0 | ||
| 14,0 | ||
| 6,0 | ||
| 5,4 | ||
| 9,0 | ||
| 15,6 | ||
| 9,0 | ||
| 8,0 | ||
| 11,5 | ||
| 5,0 | ||
| 15,0 | ||
| 13,5 | ||
| 17,0 | ||
| 10,5 | ||
| 12,0 |
Задача 52 - Имеются данные по машиностроительному заводу о проценте бракованных поршневых колес и проценте влажности формовочной смеси (по данным эксперимента в литейном цехе):
Таблица 31
| Номер плавки | Влажность смеси, % | Брак, % |
| 3,1 | 45,4 | |
| 3,0 | 32,2 | |
| 3,4 | 42,9 | |
| 3,3 | 47,3 | |
| 3,1 | 41,6 | |
| 3,2 | 36,1 | |
| Продолжение таблицы 31 | ||
| Номер плавки | Влажность смеси, % | Брак, % |
| 3,3 | 49,8 | |
| 3,2 | 44,5 | |
| 3,2 | 51,9 | |
| 3,1 | 51,9 | |
| 3,1 | 51,9 | |
| 3,0 | 28,2 | |
| 3,6 | 56,9 | |
| 3,5 | 42,6 | |
| 3,2 | 45,0 | |
| 3,1 | 42,6 | |
| 3,3 | 50,0 | |
| 3,0 | 32,2 | |
| 3,5 | 12,7 | |
| 3,6 | 57,0 |
Задача 53 - Имеются следующие данные о численности рабочих и объеме основных фондов (млн. руб.):
Таблица 32
| Номер завода | Средняя списочная численность рабочих, чел | Объем основных фондов на начало отчетного периода, млн. руб. |
| Продолжение таблицы 32 | ||
| Номер завода | Средняя списочная численность рабочих, чел | Объем основных фондов на начало отчетного периода, млн. руб. |
Задача 54 - Имеются следующие данные о качестве ковкого чугуна (относительное удлинение в процентах) и его химическом составе (содержание углерода в процентах):
Таблица 33
| Номер анализа | Содержание углерода, % | Относительное удлинение, % |
| 2,58 | 9,9 | |
| 2,55 | 10,5 | |
| 2,57 | 11,2 | |
| 2,24 | 28,9 | |
| 2,53 | 12,8 | |
| 2,64 | 13,5 | |
| 2,64 | 12,2 | |
| 2,63 | 14,2 | |
| 2,50 | 12,5 | |
| 2,57 | 13,6 | |
| 2,42 | 13,3 | |
| 2,50 | 13,9 | |
| 2,61 | 10,8 | |
| 2,55 | 9,7 | |
| 2,34 | 9,6 | |
| 2,48 | 10,7 | |
| 2,47 | 12,5 | |
| 2,24 | 10,6 | |
| 2,43 | 13,5 | |
| 2,46 | 13,4 | |
| 2,54 | 13,3 | |
| 2,53 | 12,2 | |
| 2,44 | 10,7 | |
| 2,58 | 11,7 |
Задача 55 - Имеются следующие данные о качестве ковкого чугуна (относительное удлинение в процентах) и средней дневной температуре заливки:
Таблица 34
| Номер анализа | Относительное удлинение, % | Средняя дневная температура заливки, 0С |
| 9,9 | ||
| 10,5 | ||
| 11,2 | ||
| 18,9 | ||
| 12,8 | ||
| 13,5 | ||
| 12,2 | ||
| 14,2 | ||
| 12,5 | ||
| 13,6 | ||
| 13,3 | ||
| 13,9 | ||
| 10,8 | ||
| 9,7 | ||
| 9,6 | ||
| 10,7 | ||
| 12,5 | ||
| 10,5 | ||
| 13,5 | ||
| 14,4 | ||
| 11,4 | ||
| 12,2 | ||
| 10,7 | ||
| 11,7 |
Условия для задач 56 - 60.
По материалу таблиц 26, 27, 28, 29, 30
а) построить групповую таблицу, показывающую зависимость между указанными признаками;
б) дать графическое изображение зависимости;
в) найти линейное уравнение связи;
г) оценить существенность параметров уравнения;
д) вычислить по найденному уравнению связи среднюю величину (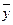
) для каждой группы в групповой таблице, сравнить вычисленные средние с эмпирическими (нанести на график).
Задача 56 - по данным условия задачи 51
-"- 57 - - " - 52
-"- 58 - - " - 53
-"- 59 - - " - 54
-"- 60 - - " - 55
ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ТИПОВЫХ ЗАДАЧ
61-70
Статистическое исследование может осуществляться по данным сплошного и не сплошного наблюдения. Наиболее распространенным методом, применяющим не сплошное наблюдение, является выборочный метод.
Под выборочным понимается метод статистического исследования, при котором обобщающие показатели совокупности устанавливаются по некоторой ее части на основе отбора. При выборочном методе обследованию подвергается небольшая часть совокупности (5-10 %, реже 20-25 %)
Совокупность, из которой производится отбор части единиц, называется генеральной совокупностью. Отобранная часть единиц из нее, подвергающаяся обследованию, называется выборочной совокупностью или просто выборкой.
Поскольку изучаемая статистическая совокупность состоит из единиц с варьирующими признаками, то состав выборки может отличаться от состава генеральной совокупности. Это расхождение составляет ошибку выборки. Способы ее определения различны в зависимости от приема формирования выборочных совокупностей и распространение характеристик выборки на генеральную совокупность составляют основное содержание методологии выборочного метода. Обобщающими характеристиками совокупностей являются средние. Средняя в генеральной совокупности обозначается -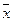 
, в выборочный - 
. В генеральной совокупности доля единиц, обладающих признаком, обозначается - р и называется генеральной долей.
В выборочной совокупности долю изучаемого признака называют выборочной долей или частотой и обозначают - w, которая определяется
,
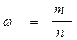где m - доля единиц, обладающих данным признаком;
n - общая численность единиц выборочной совокупности.
Отбор единиц совокупности осуществляется на основе различных способов:
- случайного,
- механического,
- типичного,
- серийного, комбинированного.
В зависимости от способа выборки и определяются следующие показатели:
- средняя ошибка,
- предельная ошибка,
- необходимая численность выборки.
Для случайного и механического отбора формулы по вычисленным показателям одинаковые, но они отличаются схемами: схемой повторной выборки, когда общая численность генеральной совокупности в процессе выборки остается неизменной, то есть единица совокупности, попавшая в выборку, после регистрации возвращается в генеральную совокупность. Повторную выборку используют редко, чаще используется схема бесповторной выборки, при которой единица совокупности, попавшая в выборку, после регистрации в генеральную совокупность не возвращается.
Средняя ошибка выборки показывает расхождения выборочной и генеральной средней.
Она определяется для бесповторного случайного отбора по формуле:
,
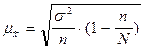для случайного повторного отбора:
,
где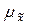 
- средняя ошибка выборочной средней;
n - численность выборки;
N - численность генеральной совокупности;
s2 - дисперсия выборочной совокупности.
Для измерения ошибки доли альтернативного признака выборочной совокупности используются другие формулы:
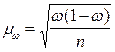(при повторном случайном отборе),
(при бесповторном случайном отборе),
где w - доля признака в выборочной совокупности;
n - численность единиц совокупности.
Эти формулы характеризуют среднюю величину отклонения сводных характеристик генеральной совокупности. Поскольку признак варьирует, следует определять предельную ошибку выборки. Она для повторного и бесповторного отбора определяется:
D = t m
где D - предельная ошибка выборки
t - кратность ошибки, коэффициент доверия, соответствующая определенной вероятности, берется по таблице значений функции Фt (приложение Б) в зависимости от значения вероятности (Р).
Значит, с определенной вероятностью можно утверждать, что отклонения выборочных характеристик от генеральных не превысят некоторой величины D и пределы, в которых находится генеральная средняя составят:
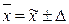
то есть генеральная средняя будет находиться в доверительном интервале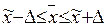 
. Доверительные границы определяются значениями лежащих по обе стороны от оценки средней наблюдений, между которыми заключен тот или иной процент площади графика распределения. Диапазон значений, в который попадает показатель генеральной совокупности с некоторой вероятностью, величина которой, как правило, устанавливается равной 95 или 99 %. Для вероятности 95 % кратность ошибки t составляет 1,96 для 99 % - t = 2,58.
Приведенные формулы для определения величины ошибки выборки дают возможность дополнительно определить численность выборки, чтобы ошибка выборки не превышала определенные заданные размеры. На практике при использовании выборочного наблюдения всегда определяют его численность по формуле:
(для повторного отбора),
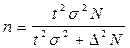(для бесповторного отбора).
Для определения доли с заданной точностью применяются следующие формулы:
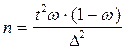(для повторного отбора),
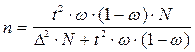(для бесповторного отбора).
Задача 61 - Сколько рабочих нужно обследовать с помощью случайной выборки для определения среднего стажа работы 4000 рабочих завода, чтобы с вероятностью, равной 0,99, утверждать, что предельная ошибка выборочной средней будет не больше одного года? Среднее квадратическое отклонение стажа по данным прошлых наблюдений равно 4,8 года.
Задача 62 - В порядке случайной выборки взято 100 проб ковкого чугуна. Лабораторный анализ этих проб дал следующие средние показатели по содержанию углерода:
- средний процент углерода - 2,5;
- среднее квадратическое отклонение - 0,15.
Определить с вероятностью 0,954 доверительные пределы среднего процента углерода в генеральной совокупности.
Задача 63 - На машиностроительных заводах области работает 25000 рабочих. В порядке случайной повторной выборки обследовано 4900 рабочих. На основе этого обследования установлено: а) среднемесячная заработная плата рабочих - 920 руб.; б) среднее квадратическое отклонение по заработной плате - 140 руб.
Определить среднюю ошибку выборки и возможные пределы средней заработной платы рабочих при вероятности 0,683.
Задача 64 - Решите предыдущую задачу при условии, что выборка организована в порядке случайного бесповторного отбора.
Задача 65 - Выборочным обследованием было охвачено 10 000 пассажиров пригородных поездов. На основе этого обследования установлена средняя дальность поездки пассажиров - 24,2 км, и среднее квадратическое отклонение 12 км. Определите возможные пределы средней дальности поездки пассажиров при вероятности 0,954 и 0,997.
Задача 66 - В порядке случайной бесповторной выборки было отобрано 5 % радиоламп из партии в 4000 шт. Среди отобранных радиолам 6 шт. оказались забракованными.
Определить:
а) долю брака по данным выборки;
б) среднюю ошибку выборочной доли;
г) доверительные пределы доли брака в генеральной совокупности с вероятностью 0,954.
Задача 67 - В результате десяти процентного выборочного обследования партии угля на процент зольности получены данные (таблица 31). Вычислить средний процент зольности по данным выборки и определить с вероятностью 0,997 границы интервала, в которых находится генеральная средняя.
Обследование производилось на основе бесповторного отбора.
Таблица 35
| % зольности угля | Число образцов |
| Итого: |
Условия для задач 68-70.
В результате десятипроцентного выборочного обследования возраста деревянных строений в трех районах получены следующие данные:
Таблица 36
| Возраст | Число выборочно обследованных строений в районе | ||
| строений | А | Б | В |
| Итого: |
Вычислить средний возраст строений по данным выборки и определить величину возможной максимальной ошибки этой средней с вероятностью, равной 0,954; обследование производилось на основе бесповторной случайной выборки.
Задачу 68 решают по данным района А.
Задачу 69 решают по данным района Б.
Задачу 70 решают по данным района В.
Список литературы
1. Альбом наглядных- пособий по общей теории статистики: учебное пособие / С.С. Сергеев, И.Д. Политова, А.П. Зинченко и др. / - М.: Финансы и статистика, 1991. - 91с.
2. Венецкий И.Г., Кильдишев Г.С. Основы теории вероятностей и математической статистики. - М.: Статистика, 1978.
3. Дружинин А.К. Математическая статистика в экономике. - М.: Статистика, 1971.
4. Ефимова М.Р. Рябцев В.М. Общая теория статистики. - М.: Финансы и статистика, 1991. - 302 с.
5. Практикум по общей теории статистики. /Под ред. Ряузова Н.А. / - М.: Статистика, 1981.
6. Ряузов Н.Н. Общая теория статистики. - М.: Статистика, 1985.
7. Практикум по теории статистики: Учеб. пособие / Под ред. проф. Р.А. Шкойловой. - М.: Финансы и статистика, 1998.
ПРИЛОЖЕНИЕ А
Таблица значений функции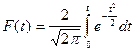 
при разных значениях t
| t | F(t) | t | F(t) | t | F(t) | t | F(t) |
| 0,00 | 0,00000 | 0,30 | 0,23582 | 0,60 | 0,45149 | 0,90 | 0,63188 |
| 0,01 | 0,00798 | 0,31 | 0,24344 | 0,61 | 0,45814 | 0,91 | 0,63718 |
| 0,02 | 0,01596 | 0,32 | 0,25103 | 0,62 | 0,46474 | 0,92 | 0,64243 |
| 0,03 | 0,02393 | 0,33 | 0,25860 | 0,63 | 0,47131 | 0,93 | 0,64763 |
| 0,04 | 0,03191 | 0,34 | 0,26614 | 0,64 | 0,47783 | 0,94 | 0,65278 |
| 0,05 | 0,03988 | 0,35 | 0,27366 | 0,65 | 0,48431 | 0,95 | 0,65789 |
| 0,06 | 0,04784 | 0,36 | 0,28115 | 0,66 | 0,49075 | 0,96 | 0,66294 |
| 0,07 | 0,05581 | 0,37 | 0,28862 | 0,67 | 0,49714 | 0,97 | 0,66795 |
| 0,08 | 0,06376 | 0,38 | 0,9605 | 0,68 | 0,50350 | 0,98 | 0,67291 |
| 0,09 | 0,07171 | 0,39 | 0,30346 | 0,69 | 0,50981 | 0,99 | 0,67783 |
| 0,10 | 0,07966 | 0,40 | 0,31084 | 0,70 | 0,51607 | 1,00 | 0,68269 |
| 0,11 | 0,8759 | 0,41 | 0,31819 | 0,71 | 0,52230 | 1,01 | 0,68750 |
| 0,12 | 0,09552 | 0,42 | 0,32552 | 0,72 | 0,52848 | 1,02 | 0,69227 |
| 0,13 | 0,10348 | 0,43 | 0,33280 | 0,73 | 0,53461 | 1,03 | 0,69699 |
| 0,14 | 0,11134 | 0,44 | 0,34006 | 0,74 | 0,54070 | 1,04 | 0,70166 |
| 0,15 | 0,11924 | 0,45 | 0,34729 | 0,75 | 0,54675 | 1,05 | 0,70628 |
| 0,16 | 0,12712 | 0,46 | 0,35448 | 0,76 | 0,55275 | 1,06 | 0,71086 |
| 0,17 | 0,13499 | 0,47 | 0,36164 | 0,77 | 0,55870 | 1,07 | 0,71538 |
| 0,18 | 0,14285 | 0,48 | 0,36877 | 0,78 | 0,56461 | 1,08 | 0,71986 |
| 0,19 | 0,15069 | 0,49 | 0,37587 | 0,79 | 0,57047 | 1,09 | 0,72429 |
| 0,20 | 0,15852 | 0,50 | 0,38292 | 0,80 | 0,57629 | 1,10 | 0,72867 |
| 0,21 | 0,16633 | 0,51 | 0,38995 | 0,81 | 0,58206 | 1,11 | 0,73300 |
| 0,22 | 0,17413 | 0,52 | 0,39694 | 0,82 | 0,58778 | 1,12 | 0,73729 |
| 0,23 | 0,18191 | 0,53 | 0,40389 | 0,83 | 0,59346 | 1,13 | 0,74152 |
| 0,24 | 0,18967 | 0,54 | 0,41080 | 0,84 | 0,59909 | 1,14 | 0,74571 |
| 0,25 | 0,19741 | 0,55 | 0,41768 | 0,85 | 0,60468 | 1,15 | 0,74986 |
| 0,26 | 0,20514 | 0,56 | 0,42452 | 0,86 | 0,61021 | 1,16 | 0,75395 |
| 0,27 | 0,21284 | 0,57 | 0,43132 | 0,87 | 0,61570 | 1,17 | 0,75800 |
| 0,28 | 0,22052 | 0,58 | 0,43809 | 0,88 | 0,62114 | 1,18 | 0,76200 |
| 0,29 | 0,22818 | 0,59 | 0,44481 | 1,89 | 0,62953 | 1,19 | 0,76595 |
| 1,20 | 0,76986 | 1,55 | 0,87886 | 1,90 | 0,94257 | 2,25 | 0,97555 |
| 1,21 | 0,77372 | 1,56 | 0,88124 | 1,91 | 0,94387 | 2,26 | 0,97618 |
| 1,22 | 0,77754 | 1,57 | 0,88358 | 1,92 | 0,94514 | 2,27 | 0,97679 |
| 1,23 | 0,78130 | 1,58 | 0,88589 | 1,93 | 0,94639 | 2,28 | 0,97739 |
| 1,24 | 0,78502 | 1,59 | 0,88817 | 1,94 | 0,94792 | 2,29 | 0,97798 |
| 1,25 | 0,78870 | 1,60 | 0,89040 | 1,95 | 0,94882 | 2,30 | 0,97855 |
| 1,26 | 0,79233 | 1,61 | 0,89260 | 1,96 | 0,95000 | 2,31 | 0,97911 |
| 1,27 | 0,79592 | 1,62 | 0,89477 | 1,97 | 0,95116 | 2,32 | 0,97966 |
| 1,28 | 0,79945 | 1,63 | 0,89690 | 1,98 | 0,95230 | 2,33 | 0,98019 |
| 1,29 | 0,80295 | 1,64 | 0,89899 | 1,99 | 0,95341 | 2,34 | 0,98072 |
| 1,30 | 0,80640 | 1,65 | 0,90106 | 2,00 | 0,95450 | 2,35 | 0,98123 |
| 1,31 | 0,80980 | 1,66 | 0,90309 | 2,01 | 0,95557 | 2,36 | 0,98172 |
| 1,32 | 0,81316 | 1,67 | 0,90508 | 2,02 | 0,95662 | 2,37 | 0,98221 |
| 1,33 | 0,81948 | 1,68 | 0,90704 | 2,03 | 0,95764 | 2,38 | 0,98269 |
| 1,34 | 0,81975 | 1,69 | 0,90897 | 2,04 | 0,95865 | 2,39 | 0,98315 |
| 1,35 | 0,82298 | 1,70 | 0,91087 | 2,05 | 0,95964 | 2,40 | 0,98360 |
| 1,36 | 0,82617 | 1,71 | 0,91273 | 2,06 | 0,96060 | 2,41 | 0,98405 |
| 1,37 | 0,82931 | 1,72 | 0,91457 | 2,07 | 0,96155 | 2,42 | 0,98448 |
| 1,38 | 0,83241 | 1,73 | 0,91637 | 2,08 | 0,96247 | 2,43 | 0,98490 |
| Продолжение приложения А | |||||||
| t | F(t) | t | F(t) | t | F(t) | t | F(t) |
| 1,39 | 0,83547 | 1,74 | 0,91814 | 2,09 | 0,96338 | 2,44 | 0,98531 |
| 1,40 | 0,83849 | 1,75 | 0,91988 | 2,10 | 0,96427 | 2,45 | 0,98571 |
| 1,41 | 0,84146 | 1,76 | 0,92159 | 2,11 | 0,96514 | 2,46 | 0,98611 |
| 1,42 | 0,84439 | 1,77 | 0,92327 | 2,12 | 0,96599 | 2,47 | 0,98649 |
| 1,43 | 0,84728 | 1,78 | 0,92492 | 2,13 | 0,96683 | 2,48 | 0,98686 |
| 1,44 | 0,85013 | 1,79 | 0,92655 | 2,14 | 0,96765 | 2,49 | 0,98723 |
| 1,45 | 0,85294 | 1,80 | 0,92814 | 2,15 | 0,96844 | 2,50 | 0,98759 |
| 1,46 | 0,85571 | 1,81 | 0,92970 | 2,16 | 0,96923 | 2,51 | 0,98793 |
| 1,47 | 0,85844 | 1,82 | 0,93124 | 2,17 | 0,96999 | 2,52 | 0,98826 |
| 1,48 | 0,86113 | 1,83 | 0,93275 | 2,18 | 0,97074 | 2,53 | 0,98859 |
| 1,49 | 0,86328 | 1,84 | 0,93423 | 2,19 | 0,97148 | 2,54 | 0,98891 |
| 1,50 | 0,86639 | 1,85 | 0,93569 | 2,20 | 0,97219 | 2,55 | 0,98923 |
| 1,51 | 0,86696 | 1,86 | 0,93711 | 2,21 | 0,97289 | 2,56 | 0,98953 |
| 1,52 | 0,87140 | 1,87 | 0,93852 | 2,22 | 0,97358 | 2,57 | 0,98983 |
| 1,53 | 0,87398 | 1,88 | 0,93989 | 2,23 | 0,97425 | 2,58 | 0,99012 |
| 1,54 | 0,87644 | 1,89 | 0,94124 | 2,24 | 0,97491 | 2,59 | 0,99040 |
| 2,60 | 0,99068 | 2,95 | 0,99682 | 3,30 | 0,99903 | 3,65 | 0,99974 |
| 2,61 | 0,99095 | 2,96 | 0,99692 | 3,31 | 0,99907 | 3,66 | 0,99975 |
| 2,62 | 0,99121 | 2,97 | 0,99702 | 3,32 | 0,99910 | 3,67 | 0,99976 |
| 2,63 | 0,99146 | 2,98 | 0,99712 | 3,33 | 0,99913 | 3,68 | 0,99977 |
| 2,64 | 0,99171 | 2,99 | 0,99721 | 3,34 | 0,99916 | 3,69 | 0,99978 |
| 2,65 | 0,99195 | 3,00 | 0,99730 | 3,35 | 0,99919 | 3,70 | 0,99978 |
| 2,66 | 0,99219 | 3,01 | 0,99739 | 3,36 | 0,99922 | 3,71 | 0,99979 |
| 2,67 | 0,99241 | 3,02 | 0,99747 | 3,37 | 0,99925 | 3,72 | 0,99980 |
| 2,68 | 0,90283 | 3,03 | 0,99755 | 3,38 | 0,99928 | 3,73 | 0,99981 |
| 2,69 | 0,99285 | 3,04 | 0,99763 | 3,39 | 0,99930 | 3,74 | 0,99982 |
| 2,70 | 0,99307 | 3,05 | 0,99771 | 3,40 | 0,99933 | 3,75 | 0,99982 |
| 2,71 | 0,99327 | 3,06 | 0,99779 | 3,41 | 0,99935 | 3,76 | 0,99983 |
| 2,72 | 0,99347 | 3,07 | 0,99786 | 3,42 | 0,99937 | 3,77 | 0,99984 |
| 2,73 | 0,99367 | 3,08 | 0,99793 | 3,43 | 0,99940 | 3,78 | 0,99984 |
| 2,74 | 0,99386 | 3,09 | 0,99800 | 3,44 | 0,99942 | 3,79 | 0,99985 |
| 2,75 | 0,99404 | 3,10 | 0,99806 | 3,45 | 0,99944 | 3,80 | 0,99986 |
| 2,76 | 0,99422 | 3,11 | 0,99813 | 3,46 | 0,99946 | 3,81 | 0,99986 |
| 2,77 | 0,99439 | 3,12 | 0,09819 | 3,47 | 0,99948 | 3,82 | 0,99987 |
| 2,78 | 0,99456 | 3,13 | 0,99825 | 3,48 | 0,99950 | 3,83 | 0,99987 |
| 2,79 | 0,99473 | 3,14 | 0,99831 | 3,49 | 0,99952 | 3,84 | 0,99988 |
| 2,80 | 0,99489 | 3,15 | 0,99837 | 3,50 | 0,99953 | 3,85 | 0,99988 |
| 2,81 | 0,99505 | 3,16 | 0,99842 | 3,51 | 0,99955 | 3,86 | 0,99989 |
| 2,82 | 0,99520 | 3,17 | 0,99848 | 3,52 | 0,99957 | 3,87 | 0,99989 |
| 2,83 | 0,99535 | 3,18 | 0,99853 | 3,53 | 0,99958 | 3,88 | 0,99990 |
| 2,84 | 0,99549 | 3,19 | 0,99858 | 3,54 | 0,99960 | 3,89 | 0,99990 |
| 2,85 | 0,99563 | 3,20 | 0,99863 | 3,55 | 0,99961 | 3,90 | 0,99990 |
| 2,86 | 0,99576 | 3,21 | 0,99867 | 3,56 | 0,99963 | 3,91 | 0,99991 |
| 2,87 | 0,99590 | 3,22 | 0,99872 | 3,57 | 0,99964 | 3,92 | 0,99991 |
| 2,88 | 0,99502 | 3,23 | 0,99876 | 3,58 | 0,99966 | 3,93 | 0,99992 |
| 2,89 | 0,99615 | 3,24 | 0,99880 | 3,59 | 0,99967 | 3,94 | 0,99992 |
| 2,90 | 0,99627 | 3,25 | 0,99855 | 3,60 | 0,99968 | 3,95 | 0,99992 |
| 2,91 | 0,99639 | 3,26 | 0,99889 | 3,61 | 0,99969 | 3,96 | 0,99992 |
| 2,92 | 0,99650 | 3,27 | 0,99892 | 3,62 | 0,99971 | 3,97 | 0,99993 |
| 2,93 | 0,99661 | 3,28 | 0,99896 | 3,63 | 0,99972 | 3,98 | 0,99993 |
| 2,94 | 0,99672 | 3,29 | 0,99800 | 3,64 | 0,99973 | 3,99 | 0,99993 |
ПРИЛОЖЕНИЕ Б
,
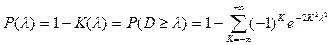| l | Р(l) | l | Р(l) | l | Р(l) | l | Р(l) | l | Р(l) |
| ³0,29 | 1,00000 | 0,76 | 0,6104 | 1,23 | 0,0970 | 1,70 | 0,0062 | 2,17 | 0,0002 |
| 0,30 | 0,99999 | 0,77 | 0,5936 | 1,24 | 0,0924 | 1,71 | 0,0058 | 2,18 | 0,0001 |
| 0,99998 | 0,78 | 0,5770 | 1,25 | 0,0879 | 1,72 | 0,0054 | 2,19 | 0,0001 | |
| 0,32 | 0,99995 | 0,79 | 0,5605 | 1,26 | 0,0836 | 1,73 | 0,0050 | 2,20 | 0,0001 |
| 0,33 | 0,99991 | 0,80 | 0,5441 | 1,27 | 0,0794 | 1,74 | 0,0047 | 2,21 | 0,0001 |
| 0,34 | 0,99983 | 0,81 | 0,5280 | 1,28 | 0,0755 | 1,75 | 0,0044 | 2,22 | 0,0001 |
| 0,35 | 0,9997 | 00,82 | 0,5120 | 1,29 | 0,0717 | 1,76 | 0,0041 | 2,23 | 0,0001 |
| 0,36 | 0,9995 | 0,83 | 0,4962 | 1,30 | 0,0681 | 1,77 | 0,0038 | 2,24 | 0,0001 |
| 0,37 | 0,9992 | 0,84 | 0,4806 | 1,31 | 0,0646 | 1,78 | 0,0035 | 2,25 | 0,0001 |
| 0,38 | 0,9987 | 0,85 | 0,4653 | 1,32 | 0,0613 | 1,79 | 0,0033 | 2,26 | 0,0001 |
| 0,39 | 0,9981 | 0,86 | 0,4503 | 1,33 | 0,0582 | 1,80 | 0,0031 | 2,27 | 0,0001 |
| 0,40 | 0,9972 | 0,87 | 0,4355 | 1,34 | 0,0551 | 1,81 | 0,0029 | 2,28 | 0,0001 |
| 0,41 | 0,9960 | 0,88 | 0,4209 | 1,35 | 0,0522 | 1,82 | 0,0027 | 2,29 | 0,0001 |
| 0,42 | 0,9945 | 0,89 | 0,4067 | 1,36 | 0,0495 | 1,83 | 0,0025 | 2,30 | 0,0001 |
| 0,43 | 0,9926 | 0,90 | 0,3927 | 1,37 | 0,0469 | 1,84 | 0,0023 | 2,31 | 0,000046 |
| 0,44 | 0,9903 | 0,91 | 0,3791 | 1,38 | 0,0444 | 1,85 | 0,0021 | 2,32 | 0,000042 |
| 0,45 | 0,9874 | 0,92 | 0,3657 | 1,39 | 0,0420 | 1,86 | 0,0020 | 2,33 | 0,000038 |
| 0,46 | 0,9840 | 0,93 | 0,3527 | 1,40 | 0,0397 | 1,87 | 0,0019 | 2,34 | 0,000035 |
| 0,47 | 0,9800 | 0,94 | 0,3399 | 1,41 | 0,0375 | 1,88 | 0,0017 | 2,35 | 0,000032 |
| 0,48 | 0,9753 | 0,95 | 0,3275 | 1,42 | 0,0354 | 1,89 | 0,0016 | 2,36 | 0,000030 |
| 0,49 | 0,9700 | 0,96 | 0,3154 | 1,43 | 0,0335 | 1,90 | 0,0015 | 2,37 | 0,000027 |
| 0,50 | 0,9639 | 0,97 | 0,3036 | 1,44 | 0,0316 | 1,91 | 0,0014 | 2,38 | 0,000024 |
| 0,51 | 0,9572 | 0,98 | 0,2921 | 1,45 | 0,0298 | 1,92 | 0,0013 | 2,39 | 0,000022 |
| 0,52 | 0,9497 | 0,99 | 0,2809 | 1,46 | 0,0282 | 1,93 | 0,0012 | 2,40 | 0,000020 |
| 0,53 | 0,9415 | 1,00 | 0,2700 | 1,47 | 0,0266 | 1,94 | 0,0011 | 2,41 | 0,000018 |
| 0,54 | 0,9325 | 1,01 | 0,2594 | 1,48 | 0,0250 | 1,95 | 0,0010 | 2,42 | 0,000016 |
| 0,55 | 0,9228 | 1,02 | 0,2492 | 1,49 | 0,0236 | 1,96 | 0,0009 | 2,43 | 0,000014 |
| 0,56 | 0,9124 | 1,03 | 0,2392 | 1,50 | 0,0222 | 1,97 | 0,0009 | 2,44 | 0,000013 |
| 0,57 | 0,9013 | 1,04 | 0,2296 | 1,51 | 0,0209 | 1,98 | 0,0008 | 2,45 | 0,000012 |
| 0,58 | 0,8896 | 1,05 | 0,2202 | 1,52 | 0,0197 | 1,99 | 0,0007 | 2,46 | 0,000011 |
| 0,59 | 0,8772 | 1,06 | 0,2111 | 1,53 | 0,0185 | 2,00 | 0,0007 | 2,47 | 0,000010 |
| 0,60 | 0,8643 | 1,07 | 0,2024 | 1,54 | 0,0174 | 2,01 | 0,0006 | 2,48 | 0,000009 |
| 0,61 | 0,8508 | 1,08 | 0,1939 | 1,55 | 0,0164 | 2,02 | 0,0006 | 2,49 | 0,000008 |
| 0,62 | 0,8368 | 1,09 | 0,1857 | 1,56 | 0,0154 | 2,03 | 0,0005 | 2,50 | 0,0000075 |
| 0,63 | 0,8222 | 1,10 | 0,1777 | 1,57 | 0,0145 | 2,04 | 0,0005 | 2,55 | 0,0000044 |
| 0,64 | 0,8073 | 1,11 | 0,1770 | 1,58 | 0,0136 | 2,05 | 0,0004 | 2,60 | 0,0000026 |
| 0,65 | 0,7920 | 1,12 | 0,1626 | 1,59 | 0,0127 | 2,06 | 0,0004 | 2,65 | 0,0000016 |
| 0,66 | 0,7764 | 1,13 | 0,1555 | 1,60 | 0,0120 | 2,07 | 0,0004 | 2,70 | 0,0000010 |
| 0,67 | 0,7604 | 1,14 | 0,1486 | 1,61 | 0,0112 | 2,08 | 0,0004 | 2,75 | 0,0000006 |
| 0,68 | 0,7442 | 1,15 | 0,1420 | 1,62 | 0,0105 | 2,09 | 0,0003 | 2,80 | 0,0000003 |
| 0,69 | 0,7278 | 1,16 | 0,1356 | 1,63 | 0,0098 | 2,10 | 0,0003 | 2,85 | 0,00000018 |
| 0,70 | 0,7112 | 1,17 | 0,1294 | 1,64 | 0,0092 | 2,11 | 0,0003 | 2,90 | 0,00000010 |
| 0,71 | 0,6945 | 1,18 | 0,1235 | 1,65 | 0,0086 | 2,12 | 0,0002 | 2,95 | 0,00000006 |
| 0,72 | 0,6777 | 1,19 | 0,1177 | 1,66 | 0,6081 | 2,13 | 0,0002 | 3,00 | 0,00000003 |
| 0,73 | 0,6609 | 1,20 | 0,1122 | 1,67 | 0,0076 | 2,14 | 0,0002 | ||
| 0,74 | 0,6440 | 1,21 | 0,1070 | 1,68 | 0,0071 | 2,15 | 0,0002 | ||
| 0,75 | 0,6272 | 1,22 | 0,1019 | 1,69 | 0,0066 | 2,16 | 0,0002 |
ПРИЛОЖЕНИЕ В
Таблица значений t Стьюдента для Р=0,05 и 0,01.
| Число степеней свободы | Р=0,05 | Р=0,01 | Число степеней свободы | Р=0,05 | Р=0,01 |
| 12,706 | 63,655 | 2,074 | 2,818 | ||
| 4,303 | 9,925 | 2,069 | 2,807 | ||
| 3,182 | 5,841 | 2,064 | 2,796 | ||
| 2,776 | 4,604 | 2,060 | 2,787 | ||
| 2,571 | 4,032 | 2,056 | 2,778 | ||
| 2,447 | 3,707 | 2,052 | 2,771 | ||
| 2,365 | 3,499 | 2,048 | 2,764 | ||
| 2,306 | 3,355 | 2,045 | 2,757 | ||
| 2,262 | 3,250 | 2,042 | 2,750 | ||
| 2,228 | 3,169 | 2,037 | 2,739 | ||
| 2,201 | 3,106 | 2,032 | 2,728 | ||
| 2,179 | 3,055 | 2,027 | 2,718 | ||
| 2,160 | 3,12 | 2,025 | 2,711 | ||
| 2,145 | 2,977 | 2,021 | 2,704 | ||
| 2,131 | 2,947 | 2,017 | 2,696 | ||
| 2,120 | 2,921 | 2,015 | 2,691 | ||
| 2,110 | 2,898 | 2,012 | 2,685 | ||
| 2,101 | 2,878 | 2,010 | 2,681 | ||
| 2,093 | 2,861 | 2,007 | 2,678 | ||
| 2,086 | 2,845 | 2,005 | 2,668 | ||
| 2,080 | 2,831 | 2,000 | 2,660 | ||
| ~ | 1,960 | 2,576 |
* Студенты, получившие задачи 21,22, 23, 24. 25 обрабатывают только один ряд, например: студент, получивший задачу 21 - ряд производства чугуна; студент, получивший задачу 22, - ряд производства стали.
** Студенты, получившие задачи 26, 27, 28, 29, 30, обрабатывают только один вариант. Например, студент, получивший задачу 26 - ряд производства чугуна и т.д.
