МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ТИПОВЫХ ЗАДАЧ
51-60
Чтобы выявить особенности в развитии явлений, обнаружить тенденции, установить зависимости, необходимо произвести группировку статистических данных. Для этой цели выбирается группировочный признак и разрабатывается система показателей сводки, которыми будут характеризоваться выделенные группы, для чего составляется макет таблицы.
Макетом таблицы называется таблица, состоящая из строк и граф, которые не заполнены цифрами. Каждая статистическая таблица (или макет) имеет подлежащее и сказуемое. Подлежащее - это объект изучения. Сказуемое - это система показателей, которыми характеризуется объект изучения. Подлежащее располагается слева в виде наименования горизонтальных строк, а сказуемое - справа, в виде наименования вертикальных граф.
В зависимости от построения подлежащего различают следующие виды таблиц: простые, групповые, комбинационные.
Групповыми таблицами называются такие, в подлежащем которых содержится группировка единиц совокупности по одному признаку.
В общественном производстве все процессы находятся в тесной взаимосвязи. Различают функциональную и корреляционную взаимосвязь между признаками. Под функциональными понимают такие взаимосвязи, при которых величина изучаемого признака определяется одним или несколькими факторами. Причем, с изменением факториальных признаков результативный признак всегда изменяется на одну и ту же величину. Однако в общественном производстве такого рода зависимости встречаются редко.
Взаимосвязи признаков экономических явлений, как правило, носят корреляционный характер. При корреляционных взаимосвязях одному значению изучаемого признака может соответствовать много значений другого или других признаков, причем, с изменением одного признака другие признаки варьируют в различных направлениях.
Различают корреляционные связи: простые и множественные (по количеству признаков связи); положительные и отрицательные (по направленности); прямолинейные и криволинейные (по аналитическому выражению).
Простая корреляция отображает связи между двумя признаками. При множественной корреляции экономическое явление рассматривается как совокупность влияния многих факторов.
Положительная корреляция отражает изменение признаков в прямой пропорциональности. Связи, когда увеличение (уменьшение) одного признака сопровождается уменьшением (увеличением) другого признака, называют отрицательными.
Прямолинейной называют связь, которая может быть выражена уравнением линейной функции. Для криволинейного вида связи, выражаемого уравнением кривой линии, характерно то, что с увеличением одного признака второй сначала увеличивается, а затем уменьшается, после достижения определенного уровня развития.
В процессе корреляционного анализа используют коэффициенты: корреляции линейной (r), корреляционного отношения (h), ассоциации (ra), взаимной сопряженности (rc), корреляции рангов (rp), множественной (rxyz), индекса корреляции (I r), регрессии (R).
Коэффициент линейной корреляции - показатель, отражающий направление и меру тесноты связи между признаками при линейных взаимосвязях (или близких к ним).
При малых выборках коэффициент линейной корреляции исчисляют по формуле:
,
или
,
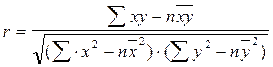где r - коэффициент корреляции;
x, y - значения изучаемых признаков;
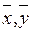- средние величины по каждому признаку;
- средняя величина произведения признаков x и y;
n - численность ряда.
Наиболее удобной формулой для расчета коэффициента корреляции является следующая:
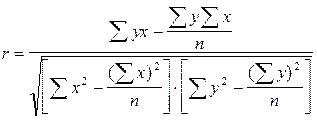
Коэффициент корреляции изменяется от -1 до +1. Чем ближе коэффициент корреляции к единице, тем связь между признаками теснее.
Существенность связи можно оценить укрупненно по таблицам Чэддока, но часто возникает необходимость дать более точную оценку существенности либо на основе t - критерия (при малых выборках), либо F критерия Фишера. Вероятностная оценка существенности коэффициента корреляции при малой выборке предпочтительно осуществляется на основе расчета значения t - критерия Стьюдента
,
где r - коэффициент корреляции;
n - число сопоставляемых пар наблюдений.
Полученное расчетное значение t - критерия Стьюдента сравнивают с его теоретической величиной в зависимости от 5% и 1% уровень значимости и n-1 числа степеней свободы (приложение В).
Если tрасч. > tтабл., то связь между фактором и результатом существенная и наоборот, если tрасч.< tтабл., то связь несущественная и данный фактор исключается из дальнейшего исследования.
Если численность выборки более 30, то вначале определяется случайная ошибка выборочного коэффициента корреляции по формуле:
,
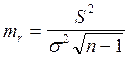где 
2 - общая дисперсия;
S2 - дисперсия разностей между эмпирическими данными и линией регрессии (остаточная дисперсия).
,
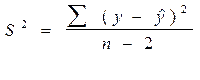где y - эмпирические значения результативного 
признака;
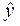- расчетные значения результативного признака.
Расчетные значения t - критерия Стьюдента определится:
tрасч.=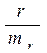 
Далее сравнение расчетной величины с табличным значением t - критерия осуществляется аналогично вышеописанному.
В процессе изучения явления важно установить не только тесноту связи, но и рассчитать показатели, характеризующие взаимосвязь между признаками. Это осуществляется с помощью решения определенных регрессионных уравнений. Для аналитического выражения прямолинейной регрессии используют формулу прямой линии:
,
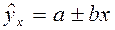где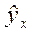 
- выровненное значение результативного признака;
a, b - параметры, представляющие средние значения постоянных показателей;
Параметры уравнения a и b определяют на основе метода наименьших квадратов, для чего решают систему нормальных уравнений.
.
Расчеты производятся в табличной форме, в которой подсчитываются значения å х, å y, å x2, å xy.
После нахождения параметров а и b записывается параметризованное уравнение прямой линии.
Параметры а и b должны быть оценены по статистическим критериям (t - критерий Стьюдента, F - критерий Фишера). Особое внимание должно быть уделено параметру b, называемому коэффициентом регрессии. Это связано с тем, что этот показатель, являясь мерой изменений зависимого признака, рассматриваемого как фактор, приобретает значения основания для операции экстраполирования.
Оценка существенности параметра b производиться на основе ошибки коэффициента регрессии:
,
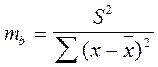где S2 - остаточная дисперсия;
x - варианты ряда (факторный признак);
- среднее значение ряда;
Расчетное значение t - критерия определяется:
.
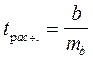Расчетное значение t - критерия сравнивается с его теоретическим значением по таблицам Стьюдента (приложение В) при n-2 степенях свободы при 5% и 1% уровне значимости. Если tрасч.>tтабл., то параметр b существенном.
Параметр а оценивается по формуле:
.
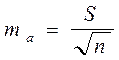Расчетное значение t - критерия для параметра a определяется:
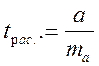
Аналогично с вышеописанным оно сравнивается с теоретическим значением и делается вывод о существенности параметра а.
