Следствие. Сумма 
степенного ряда (9) является бесконечно дифференцируемой (т.е. имеет производные любого порядка) функцией на интервале сходимости этого ряда 
.
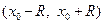С помощью приведенной выше теоремы можно находить области сходимости и (что наиболее важно) формулы для сумм некоторых степенных (или числовых) рядов. Для этого с помощью интегрирования или дифференцирования исследуемых рядов получают степенной ряд с известной суммой (например, геометрическую прогрессию), т.е. получают формульное выражение для производной или интеграла от искомой суммы 
. а затем по этому выражению восстанавливают и саму функцию .
Пример 5. Найти интервал сходимости и сумму степенного ряда
(13) 
.
Решение. Обозначим через 
сумму этого ряда, пусть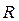 
− его радиус сходимости. Тогда выполнено: 
для всех точек из интервала сходимости 
. Тогда по формуле (11):
(14) 
.
Степенной ряд в правой части (14) 
при каждом числе 
представляет собой геометрическую прогрессию с первым членом и знаменателем прогрессии 
. В параграфе «Числовые ряды – основные понятия» мы уже рассматривали условия сходимости геометрической прогрессии и получили, что она сходится только при условии 
. Поэтому областью сходимости ряда 
является интервал (−1, 1), а для всех из этого интервала сумма ряда (по формуле суммы бесконечной убывающей геометрической прогрессии – формула (6) в параграфе «Числовые ряды – основные понятия») равна 
. Таким образом, по приведенной выше теореме о почленном дифференцировании и интегрировании степенного ряда интервал сходимости исходного ряда (13) тоже (−1, 1). Подставляя в правую часть (14), получаем 
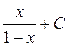. Отсюда следует, что функция 
является одной из первообразных для 
, а потому 
. Итак, мы нашли выражение для суммы степенного ряда (13):
(15) 
, 
.
Пример 6. Найти сумму числового ряда
(16) 
.
Решение. Рассмотрим вспомогательный степенной ряд 
, сумму которого обозначим :
(17) 
.
Найдем формулу для , а тогда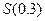 
даст нам искомую сумму ряда (17). Вычислим производную функции в (17), используя формулу (10) почленного дифференцирования ряда:
(18) 
.
Для степенного ряда в правой части (18) мы уже находили сумму и область сходимости (см. параграф «Функциональные ряды», формула (5)): 
для всех 
. Поэтому из (18) получаем, что 
для . Таким образом, функция оказывается одной из первообразных функции . Найдем множество всех первообразных этой функции (т.е. неопределенный интеграл от нее), а затем среди них найдем и : 
. Таким образом, получили, что для :
(19) 
при некотором значении произвольной постоянной 
. Найдем это значение . Из (17) следует, что значение функции при 
будет 
. Таким образом, 
, а потому из (19): 
, откуда 
. Поэтому из (19) получаем, что 
для всех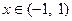 
. А потому 
. Итак, 
.
Разложение функций в степенные ряды
Используя формулу для суммы бесконечно убывающей геометрической прогрессии, мы в параграфе «Функциональные ряды» (формула (5)) получили, что сумма степенного ряда 
для всех . Если теперь поменять местами левую и правую часть этого равенства, то получится, что выполнено равенство
(1) 
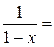
для всех .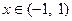
Это означает, что функция 
представлена на интервале 
в виде сходящегося степенного ряда. А для каких еще функций возможно такое представление? И как его найти?
Введем следующее определение. Будем говорить, что функция 
разлагается в степенной ряд с центром в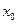 
на интервале 
, если для всех из этого интервала справедливо равенство
(2) 
.
Теперь заданные выше вопросы можно переформулировать следующим образом. Какие функции разлагаются в степенные ряды с центром в некоторой точке 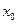и (если разложение возможно) как найти коэффициенты 
этого разложения?
В предыдущем параграфе было сформулировано следствие о том, что сумма степенного ряда является бесконечно дифференцируемой функцией на интервале сходимости ряда. Поэтому разлагаться в степенной ряд могут только функции (да и то не все!), имеющие производные любого порядка. Пусть некоторая функция имеет производные любого порядка в некоторой окрестности точки 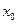. Найдем значения самой функции и всех ее производных (по предположению они существуют!) в этой точке: 
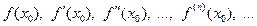. Теперь, используя эти числа, составим следующий степенной ряд:
(3) 
=
.
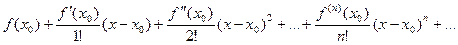Этот ряд называется рядом Тейлора функции 
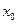с центром в точке . Таким образом, каждой бесконечно дифференцируемой в окрестности точки 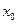функции можно поставить в соответствие некоторый степенной ряд − ее ряд Тейлора. Оказывается, что уж если функция разлагается в окрестности некоторой точки в какой-либо степенной ряд, то этот ряд может быть только рядом Тейлора этой функции. Об этом говорит следующая
Теорема (о единственности разложения в степенной ряд). Пусть функция разлагается в окрестности точки 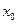в степенной ряд:
(4) 
.
Тогда она бесконечно дифференцируема в окрестности этой точки и
(5) 
.
Доказательство. Бесконечная дифференцируемость функции , являющейся суммой степенного ряда, уже отмечалась в предыдущем параграфе. Подставив в правую и левую части равенства (4)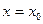 
, получим первую из формул в (5). Дифференцируя почленно степенной ряд в (4) (а это можно делать с суммой степенного ряда!), получим 
. Снова подставляя в это равенство 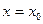, получим вторую из формул в (5). Снова дифференцируя это равенство и подставляя 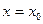, получим третью формулу в (5). И так далее, что завершает доказательство теоремы.
Формулы (5) и дают ответ на вопрос о способе нахождения коэффициентов разложения функции в степенной ряд (коли такое разложение вообще возможно). Теперь ответим на вопрос о том, для каких функций гарантирована возможность такого разложения.
Теорема (о разложении). Если функция бесконечно дифференцируема в некотором интервале 
и ее производные всех порядков ограничены на этом интервале одним и тем же числом (т.е. в формальной записи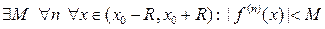 
), то она разлагается в свой ряд Тейлора на этом интервале, т.е. для всех 
имеет место представление:
(6) 
Особенно просто ряд Тейлора (3) для функции выглядит при 
:
= 
.
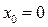В этом случае ряд Тейлора называется рядом Маклорена для функции . Учитывая (6), находим вид разложения функции в ряд Маклорена ():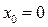
(7) 
.
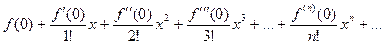Согласно приведенной выше теореме о разложении, представление (7) функции в виде ряда Маклорена имеет место на любом интервале вида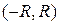 
, если только функция бесконечно дифференцируема в интервале 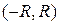и ее производные всех порядков ограничены на этом интервале одним и тем же числом.
Разложение функций в ряд Маклорена применяется значительно чаще, поскольку представляет собой удобное для приложений разложение функции по степеням (т.е. представляет собой многочлен «бесконечной степени»). Найдем разложения в ряд Маклорена некоторых основных элементарных функций.
