(11) 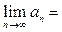



 .
.
Ясно, что в числителе  . Найдем предел выражения
. Найдем предел выражения  :
: 

 ={применяем правило Лопиталя раскрытия неопределенностей в пределах}=
={применяем правило Лопиталя раскрытия неопределенностей в пределах}= 




 . Итак,
. Итак, 
 , а потому из (11) следует
, а потому из (11) следует 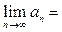
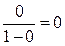 , т.е выполнение свойства (9). Таким образом, ряд (5) действительно является знакочередующимся рядом, к которому применим признак Лейбница, а потому ряд (5) сходится.
, т.е выполнение свойства (9). Таким образом, ряд (5) действительно является знакочередующимся рядом, к которому применим признак Лейбница, а потому ряд (5) сходится.
Знакопеременные ряды
Переходим теперь к изучению рядов с произвольным распределением знаков его слагаемых. Пусть дан ряд
(1) 
с произвольными по знаку слагаемыми  . Опять нужно исследовать его на сходимость. Поскольку большинство пройденных нами признаков сходимости-расходимости касались положительных рядов, то попробуем составить по данному ряду вспомогательный положительный ряд, для которого сможем применить эти признаки. Вспомогательный положительный ряд для ряда (1) построим так: положительные слагаемые оставим на месте, а у отрицательный поменяем знак. То же самое делает взятие модуля от числа (положительное число оставляет на месте, а у отрицательного поменяет знак), поэтому вспомогательный положительный ряд есть ряд, составленный из модулей слагаемых:
. Опять нужно исследовать его на сходимость. Поскольку большинство пройденных нами признаков сходимости-расходимости касались положительных рядов, то попробуем составить по данному ряду вспомогательный положительный ряд, для которого сможем применить эти признаки. Вспомогательный положительный ряд для ряда (1) построим так: положительные слагаемые оставим на месте, а у отрицательный поменяем знак. То же самое делает взятие модуля от числа (положительное число оставляет на месте, а у отрицательного поменяет знак), поэтому вспомогательный положительный ряд есть ряд, составленный из модулей слагаемых:
(2) 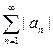
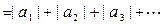 .
.
Допустим, что имеющимися признаками для положительных рядов мы узнали, сходится ряд (2) или расходится. Можно ли теперь ответить на вопрос о сходимости или расходимости исходного ряда (1)? Иногда да, а иногда нет. Поскольку справедлива следующая
Теорема. Если ряд (2) сходится, то сходится и ряд (1).
А вот если ряд из модулей (2) расходится, то о сходимости или расходимости ряда (1) ничего сказать нельзя. Может быть всякое.
В связи с этим для знакопеременного ряда (1) могут возникнуть только 3 взаимоисключающие ситуации.
1. Ряд (2) сходится. В этом случае (по теореме) сходится и ряд (1), который в этом случае называется абсолютно сходящимся рядом. Этим подчеркивается, что сходится не только этот ряд, но и ряд, составленный из абсолютных величин (т.е. модулей) слагаемых ряда.
2. Ряд (2) расходится, но, тем не менее, сам ряд (1) сходится. В этом случае ряд (1) называется условно сходящимся рядом. Этим подчеркивается, что сходится только сам ряд, но ряд, составленный из абсолютных величин слагаемых ряда, расходится.
3. Исходный ряд (1) расходится. Конечно, расходится при этом и ряд из модулей (2) (т.к. если бы он сходился, то по теореме сходился бы и исходный ряд).
Поэтому, когда ставится вопрос об исследовании сходимости произвольного знакопеременного ряда, то ответом будет являться одно из: а) ряд сходится абсолютно; б) ряд сходится условно; в) ряд расходится.
Пример 1. Ряд 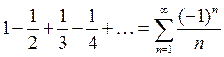 сходится условно. Это следует из того, что сам ряд сходится (это было доказано в примере 1 предыдущего параграфа), а составленный из модулей ряд суть гармонический
сходится условно. Это следует из того, что сам ряд сходится (это было доказано в примере 1 предыдущего параграфа), а составленный из модулей ряд суть гармонический  , который расходится.
, который расходится.
Пример 2. Ряд 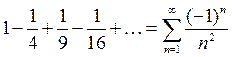 сходится абсолютно. Это следует из того, что сходится составленный из модулей ряд
сходится абсолютно. Это следует из того, что сходится составленный из модулей ряд  ,
,
поскольку это ряд вида  при
при  (см. пример 8 параграфа «Положительные ряды»).
(см. пример 8 параграфа «Положительные ряды»).
Пример 3. Ряд 
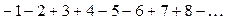 расходится, так как общий член ряда, очевидно, не стремиться к 0.
расходится, так как общий член ряда, очевидно, не стремиться к 0.
Для исследования ряда на абсолютную сходимость может помочь следующая
Теорема (обобщенный признак Даламбера). Пусть дан произвольный ряд  . Пусть существует конечный или бесконечный предел
. Пусть существует конечный или бесконечный предел  . Тогда при l < 1 ряд абсолютно сходится, а при l > 1 ряд расходится.
. Тогда при l < 1 ряд абсолютно сходится, а при l > 1 ряд расходится.
Этот признак может быть использован в дальнейшем и для исследования так называемых степенных рядов.
Функциональные ряды
Складывать можно не только бесконечно много чисел, но и бесконечно много функций. Пусть  − бесконечный набор некоторых функций. Выражение вида
− бесконечный набор некоторых функций. Выражение вида
(1) 
называется функциональным рядом. Если в каждую из этих функций подставить конкретное (допустимое) значение  и вычислить ее значение, затем подставить в функциональный ряд (1), то он перейдет в числовой ряд. При подстановке некоторых значений
и вычислить ее значение, затем подставить в функциональный ряд (1), то он перейдет в числовой ряд. При подстановке некоторых значений  получающийся числовой ряд может оказаться сходящимся, а некоторых − расходящимся.
получающийся числовой ряд может оказаться сходящимся, а некоторых − расходящимся.
Областью сходимости функционального ряда (1) называется множество всех чисел х, при подстановке которых в этот ряд получается сходящийся числовой ряд.
Пусть D − область сходимости ряда (1). Тогда для всех  из D ряд (1) сходится, а потому имеет некоторое число S в качестве своей суммы. При разных
из D ряд (1) сходится, а потому имеет некоторое число S в качестве своей суммы. При разных  сумма ряда S может быть различной, а потому сумма ряда является некоторой функцией от
сумма ряда S может быть различной, а потому сумма ряда является некоторой функцией от  :
:  . Тогда можно записать, что для всех
. Тогда можно записать, что для всех  из D:
из D:
(2)  .
.
Пример 1. Найти область сходимости ряда
(3)  .
.
Решение. Ряд (3) это функциональный ряд вида (1) при  . Нужно выяснить, при подстановке каких числовых значений
. Нужно выяснить, при подстановке каких числовых значений  в (3) получается сходящийся числовой ряд. Ранее (в параграфе «Положительные ряды», пример 8) мы уже рассматривали подобные числовые ряды вида
в (3) получается сходящийся числовой ряд. Ранее (в параграфе «Положительные ряды», пример 8) мы уже рассматривали подобные числовые ряды вида  и выяснили, что они сходятся только при условии
и выяснили, что они сходятся только при условии  . Отсюда следует, что и ряд (3) сходится только при
. Отсюда следует, что и ряд (3) сходится только при  . Поэтому областью сходимости D данного ряда является интервал
. Поэтому областью сходимости D данного ряда является интервал  .
.
Пример 2. Найти область сходимости ряда
(4) 
и выражение для суммы этого ряда  .
.
Решение. При подстановке любого числа  в (4) получается, как легко видеть, геометрическая прогрессия с первым членом 1 и со знаменателем прогрессии
в (4) получается, как легко видеть, геометрическая прогрессия с первым членом 1 и со знаменателем прогрессии  . В параграфе «Числовые ряды – основные понятия» мы уже рассматривали условия сходимости геометрической прогрессии и получили, что она сходится только при условии
. В параграфе «Числовые ряды – основные понятия» мы уже рассматривали условия сходимости геометрической прогрессии и получили, что она сходится только при условии  . Поэтому областью сходимости ряда (4) является интервал
. Поэтому областью сходимости ряда (4) является интервал  , а для всех
, а для всех  из этого интервала сумма ряда (по формуле суммы бесконечной убывающей геометрической прогрессии – формула (6) в параграфе «Числовые ряды – основные понятия») равна:
из этого интервала сумма ряда (по формуле суммы бесконечной убывающей геометрической прогрессии – формула (6) в параграфе «Числовые ряды – основные понятия») равна:  . Таким образом,
. Таким образом,
(5) 
 для всех
для всех  .
.
Степенные ряды
Более подробно рассмотрим специальные функциональные ряды  , для которых слагаемые
, для которых слагаемые  имеют вид:
имеют вид:  , где
, где 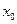 − некоторое число, а
− некоторое число, а 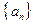 − некоторая заданная последовательность чисел. Итак, степенным рядом с центром в точке
− некоторая заданная последовательность чисел. Итак, степенным рядом с центром в точке 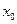 называется функциональный ряд вида
называется функциональный ряд вида
(1) 
 .
.
Числа  называются коэффициентами степенного ряда.
называются коэффициентами степенного ряда.
Пример 1. Функциональный ряд
 .
.
является степенным рядом с центром в точке  , а его коэффициенты
, а его коэффициенты  ,
,  .
.
Проще всего выглядит степенной ряд (1) с центром в нуле, т.е. когда  :
:
(2)  .
.
Этот ряд можно рассматривать как многочлен бесконечной степени. Ряд (1) с переменной  всегда можно свести к ряду (2), сделав в нем замену переменной
всегда можно свести к ряду (2), сделав в нем замену переменной 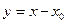 . Тогда получится ряд вида (2) с переменной у.
. Тогда получится ряд вида (2) с переменной у.
Степенной ряд (1) всегда имеет непустую область сходимости, так как число 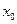 (для ряда (2) это число 0) всегда входит в эту область, поскольку при
(для ряда (2) это число 0) всегда входит в эту область, поскольку при 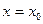 степенной ряд (1) обрывается на первом слагаемом (остальные слагаемы зануляются), а потому сходится и сумма его равна
степенной ряд (1) обрывается на первом слагаемом (остальные слагаемы зануляются), а потому сходится и сумма его равна  .
.
Область сходимости степенного ряда (1) имеет специфическую структуру − это либо только одна точка 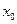 , либо некоторый интервал с центром в этой точке (концы интервала могут входить или не входить в эту область), либо вся числовая прямая (которая, при желании, может тоже рассматриваться как бесконечный интервал с центром в точке
, либо некоторый интервал с центром в этой точке (концы интервала могут входить или не входить в эту область), либо вся числовая прямая (которая, при желании, может тоже рассматриваться как бесконечный интервал с центром в точке 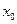 ). А именно, справедлива следующая
). А именно, справедлива следующая
Теорема (об области сходимости степенного ряда). Областью сходимости степенного ряда (1) является либо одно число 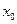 , либо вся числовая прямая, либо интервал вида
, либо вся числовая прямая, либо интервал вида 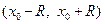 и, возможно, одна или обе концевых точки этого интервала.
и, возможно, одна или обе концевых точки этого интервала.
Интервал 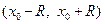 , фигурирующий в теореме, называется интервалом сходимости степенного ряда (1), а число
, фигурирующий в теореме, называется интервалом сходимости степенного ряда (1), а число  называется радиусом сходимости этого ряда. Для всех значений
называется радиусом сходимости этого ряда. Для всех значений  внутри интервала сходимости степенной ряд (1) сходится абсолютно. Для ряда (2) (случай
внутри интервала сходимости степенной ряд (1) сходится абсолютно. Для ряда (2) (случай  ) интервал сходимости имеет вид
) интервал сходимости имеет вид  .
.
Радиус сходимости может быть вычислен по одной из следующих формул:
(3) 
или
(4)  ,
,
если, конечно, соответствующие пределы существуют. Доказательство теоремы, а также формула (3) для радиуса сходимости могут быть получены несложными рассуждениями из обобщенного признака Даламбера, приведенного в конце параграфа «Знакопеременные ряды», но здесь мы на этом останавливаться не будем.
Если по (3) или (4) получается  , то область сходимости состоит только из одной точки
, то область сходимости состоит только из одной точки 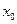 . Если же
. Если же  , то областью сходимости является вся числовая прямая.
, то областью сходимости является вся числовая прямая.
Для нахождения области сходимости произвольного степенного ряда  применяется следующая схема.
применяется следующая схема.
1) Находим интервал сходимости ряда 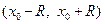 . Для этого либо вычисляется радиус сходимости
. Для этого либо вычисляется радиус сходимости  по приведенным выше формулам, либо напрямую применяется обобщенный признак Даламбера, приведенный в конце параграфа «Знакопеременные ряды». Этот признак удобнее применять тогда, когда в степенном ряде бесконечно много коэффициентов { an } обращаются в 0, а потому вычисление радиуса сходимости по формуле (3) или (4) невозможно. Это происходит, например, тогда, когда ряд содержит только четные (либо только нечетные) степени
по приведенным выше формулам, либо напрямую применяется обобщенный признак Даламбера, приведенный в конце параграфа «Знакопеременные ряды». Этот признак удобнее применять тогда, когда в степенном ряде бесконечно много коэффициентов { an } обращаются в 0, а потому вычисление радиуса сходимости по формуле (3) или (4) невозможно. Это происходит, например, тогда, когда ряд содержит только четные (либо только нечетные) степени 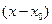 , что означает, что в (1) все коэффициенты
, что означает, что в (1) все коэффициенты  при нечетных (соответственно, четных) показателях степени
при нечетных (соответственно, четных) показателях степени 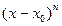 обращаются в ноль.
обращаются в ноль.
2) Проверяем принадлежность концевых точек интервала сходимости  и
и  области сходимости. Для этого подставляем каждое из этих чисел в исходный степенной ряд (вместо
области сходимости. Для этого подставляем каждое из этих чисел в исходный степенной ряд (вместо  ) и исследуем на сходимость получившийся числовой ряд. Если ряд оказался сходящимся, то проверяемая граница интервала сходимости принадлежит области сходимости, а если нет − то нет.
) и исследуем на сходимость получившийся числовой ряд. Если ряд оказался сходящимся, то проверяемая граница интервала сходимости принадлежит области сходимости, а если нет − то нет.
3) Выписываем область сходимости как интервал сходимости с возможным включением его концевых точек (в зависимости от результатов пункта 2)).
Пример 2. Найти область сходимости степенного ряда
(5)  .
.
Решение. Поскольку 
 , то ряд (5) есть степенной ряд вида (1) с центром в точке
, то ряд (5) есть степенной ряд вида (1) с центром в точке  и коэффициентами
и коэффициентами  . Согласно приведенной выше схеме нахождения области сходимости степенного ряда, сначала вычислим радиус сходимости по формуле (3). В данном примере
. Согласно приведенной выше схеме нахождения области сходимости степенного ряда, сначала вычислим радиус сходимости по формуле (3). В данном примере
(6)  ,
,
поскольку  при любом натуральном числе n принимает значение либо 1, либо (−1), а выражение
при любом натуральном числе n принимает значение либо 1, либо (−1), а выражение  всегда положительно. Подставляя в (6) выражение
всегда положительно. Подставляя в (6) выражение  вместо
вместо  , получим выражение для
, получим выражение для  :
:  . Тогда по формуле (3) радиус сходимости
. Тогда по формуле (3) радиус сходимости



 =
=
 =
=  .
.
Таким образом,  . Поэтому интервалом сходимости
. Поэтому интервалом сходимости 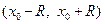 будет в данном случае интервал
будет в данном случае интервал  . Область сходимости состоит из точек этого интервала и, возможно, одной или обеих граничных точек этого интервала
. Область сходимости состоит из точек этого интервала и, возможно, одной или обеих граничных точек этого интервала 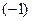 и
и  . Проверим эти точки на принадлежность области сходимости ряда (5). Для этого (по определению области сходимости ряда) будем подставлять эти числа вместо
. Проверим эти точки на принадлежность области сходимости ряда (5). Для этого (по определению области сходимости ряда) будем подставлять эти числа вместо  в (5) и выяснять, будет ли получающийся при этом числовой ряд сходящимся или расходящимся.
в (5) и выяснять, будет ли получающийся при этом числовой ряд сходящимся или расходящимся.
Рассмотрим сначала 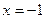 . Подставляя
. Подставляя 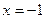 в ряд (5) получим числовой ряд:
в ряд (5) получим числовой ряд: 
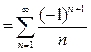
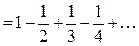 . Этот знакочередующийся ряд уже был рассмотрен в параграфе «Знакочередующиеся ряды» (пример 1) и по признаку Лейбница было доказано, что он сходится. Поэтому число
. Этот знакочередующийся ряд уже был рассмотрен в параграфе «Знакочередующиеся ряды» (пример 1) и по признаку Лейбница было доказано, что он сходится. Поэтому число 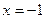 будет включаться в область сходимости ряда (5).
будет включаться в область сходимости ряда (5).
Рассмотрим другую граничную точку интервала сходимости 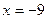 . Подставляя
. Подставляя 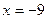 в ряд (5) получим числовой ряд:
в ряд (5) получим числовой ряд: 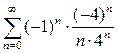 . Упростим выражение для общего члена полученного ряда:
. Упростим выражение для общего члена полученного ряда: 


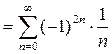
 .
.
При этом выводе мы воспользовались тем, что 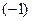 в четной степени
в четной степени  всегда дает
всегда дает 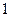 . Полученный гармонический ряд
. Полученный гармонический ряд 
 , как неоднократно было заявлено, расходится. Поэтому число
, как неоднократно было заявлено, расходится. Поэтому число 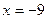 не будет включаться в область сходимости ряда (5). Таким образом, областью сходимости ряда (5) является полуинтервал
не будет включаться в область сходимости ряда (5). Таким образом, областью сходимости ряда (5) является полуинтервал  .
.
Пример 3. Найти область сходимости степенного ряда
(7)  .
.
Решение. Ряд (7) есть степенной ряд вида (1) с центром в точке  (т.е. ряд вида (2)) и коэффициентами
(т.е. ряд вида (2)) и коэффициентами  . Согласно приведенной выше схеме нахождения области сходимости степенного ряда, сначала вычислим радиус сходимости по формуле (3). В данном примере
. Согласно приведенной выше схеме нахождения области сходимости степенного ряда, сначала вычислим радиус сходимости по формуле (3). В данном примере 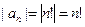 , а потому
, а потому 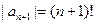 . Тогда по формуле (3) радиус сходимости
. Тогда по формуле (3) радиус сходимости 

 =
=  . Таким образом, радиус
. Таким образом, радиус  . В этом случае (как выше сказано) область сходимости состоит из единственной точки
. В этом случае (как выше сказано) область сходимости состоит из единственной точки  .
.
Пример 4. Найти область сходимости степенного ряда
(8)  .
.
Решение. Ряд (8) есть степенной ряд вида (1) с центром в точке  (т.е. опять ряд вида (2)) и коэффициентами
(т.е. опять ряд вида (2)) и коэффициентами  . Вычислим радиус сходимости по формуле (3). В данном примере
. Вычислим радиус сходимости по формуле (3). В данном примере  , а потому
, а потому 
 . Тогда по формуле (3) радиус сходимости
. Тогда по формуле (3) радиус сходимости 

 =
=  . Таким образом, радиус сходимости
. Таким образом, радиус сходимости 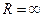 . В этом случае (как выше сказано) областью сходимости является вся числовая прямая
. В этом случае (как выше сказано) областью сходимости является вся числовая прямая  .
.
Рассмотрим теперь свойства функции  , являющейся суммой степенного ряда (1) и определенной на его области сходимости:
, являющейся суммой степенного ряда (1) и определенной на его области сходимости:
(9) 
Теорема (о почленном дифференцировании и интегрировании степенного ряда). Сумма (9) степенного ряда  является непрерывной функцией на интервале сходимости
является непрерывной функцией на интервале сходимости 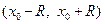 . Внутри этого интервала степенной ряд можно почленно дифференцировать и брать неопределенный интеграл. Получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный степенной ряд.
. Внутри этого интервала степенной ряд можно почленно дифференцировать и брать неопределенный интеграл. Получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный степенной ряд.
Утверждение о возможности почленного дифференцирования и интегрирования степенного ряда означают справедливость следующих формул:
(10) 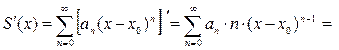

(11) 
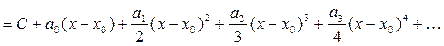
Произвольная постоянная  возникла (как и должно быть) при вычислении неопределенного интеграла (только здесь ее удобно записать в начале, а не в конце.
возникла (как и должно быть) при вычислении неопределенного интеграла (только здесь ее удобно записать в начале, а не в конце.
По утверждению теоремы сумма (9) степенного ряда  является дифференцируемой (т.е. имеющей производную) функцией на интервале сходимости
является дифференцируемой (т.е. имеющей производную) функцией на интервале сходимости 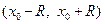 . После вычисления ее производной по формуле (10) эта производная
. После вычисления ее производной по формуле (10) эта производная  опять представляется суммой степенного ряда
опять представляется суммой степенного ряда 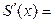
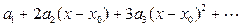 с тем же интервалом сходимости
с тем же интервалом сходимости 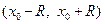 . А потому от функции
. А потому от функции  опять можно вычислять производную (будет получаться уже вторая производная
опять можно вычислять производную (будет получаться уже вторая производная  ), которая опять будет представляться степенным рядом на интервале
), которая опять будет представляться степенным рядом на интервале 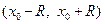 . И так далее. Отсюда вытекает важное
. И так далее. Отсюда вытекает важное






