матрица, составленная из алгебраических дополнений для элементов исходной матрицы.
Где:
- C * — союзная матрица;
- Aij — алгебраическое дополнение.
Элементарные преобразования матриц
1. умножение строки или столбца матрицы на ненулевое число;
2. перестановка местами двух строк или столбцов матрицы;
3. прибавление к некоторой строке матрицы другой ее строки, предварительно умноженной на произвольный коэффициент;
4. прибавление к некоторому столбцу матрицы другого ее столбца, предварительно умноженного на произвольный коэффициент.
Ранг матрицы.
Рангом матрицы А называется наивысший порядок минора матрицы А, отличного от нуля.
Вычисляется:
1)Умножение строки(столбца на числ, отличное от нуля.
2)Прибавление к одной строке(столбцу) другой, умножение на любое число.
3)Перемена местами двух строк(столбцов)
4)Вычёркивание нулевой строки
Базисные строки и столбцы
Столбцы и строки, на которых расположены элементы базисного минора
14.Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
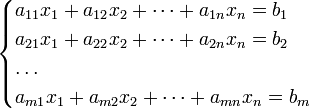Теорема Кронекера – Капели
Теорема Кронекера — Капе́лли —Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
|
Метод Крамера
При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:
(i = 1, 2, …, m). Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц Ai, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов. Так А1 получается из матрицы А заменой первого столбца на столбец правых частей f.
Метод Гаусса
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Решить систему уравнений методом Гаусса:
x + y - 3z = 2,
3x - 2y + z = - 1,
2x + y - 2z = 0.
Решение. Выпишем расширенную матрицу данной системы
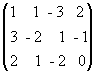
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
~ 
;
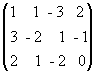б) третью строку умножим на (-5) и прибавим к ней вторую:
.
В результате всех этих преобразований данная система приводится к треугольному виду:
x + y - 3z = 2,
-5y + 10z = -7,
- 10z = 13.
Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим
x = - 0,7.
16. Метод обратной матрицы решения систем алгебраических уравнений Если det A ≠ 0, то существует обратная матрица 
. Тогда решение СЛАУ записывается в виде: 
. Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.
