Нелинейные свойства усилителей, зависящие от таких опасных в них нелинейных явлений как интермодуляция и блокирование, в технической литературе определяются и анализируются различным образом. Классический анализ опирается в основном на методике, основанной на разложении в ряд Тейлора функции, выражающей зависимость выходного тока от напряжения на управляющем электроде усилительного прибора при сопротивлении нагрузки Rн = 0. При этом оказываются неучтенными нелинейность выходных сопротивлений, а также упомянутое сопротивление нагрузки. Последнее обстоятельство приводит к недопустимо большим погрешностям в количественной оценке продуктов нелинейного преобразования (ПНП), а, следовательно, делает указанный метод практически непригодным для анализа нелинейных явлений, в особенности, при больших реальных уровнях помех на входе усилителя.
В [4, 5] показано, что при таких условиях наиболее целесообразно использовать методику анализа, основанную на разложении мгновенного коэффициента передачи (МКП) k (t) в ряд Тейлора, коэффициенты которого представляются в виде рядов Фурье по частоте помехи. Затем, выделив фильтром соответствующие спектральные составляющие выходного сигнала и воспользовавшись аппроксимацией реальной характеристики передачи усилительного прибора, находят постоянную составляющую и амплитуды соответствующих гармоник спектра, а, следовательно, соответствующие коэффициенты и параметры нелинейности.
Так, под воздействием аддитивно действующих на входе усилителя на ПТ мгновенных значений гармонических напряжений полезного сигнала uс и помехи uп при выбранном постоянном напряжении смещения между затвором и истоком Uсм = Uзи мгновенный коэффициент передачи усилителя запишется следующим образом:
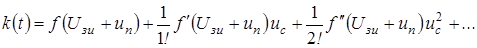, (4.1)
где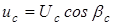 
; 
; 
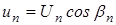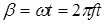– текущая фаза соответствующего напряжения; Uс и Uп – амплитуды напряжений; Uс < Uп; Uс << Uзи.
В результате разложения функции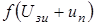 
и ее первой 
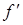и второй 
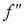производных в ряд Фурье по частоте помехи и последующих тригонометрических преобразований получим выражения для упомянутых амплитуд напряжений соответствующих гармоник спектра, коэффициентов и параметров нелинейности:
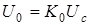, (4.2)
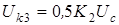, (4.3)
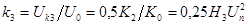, (4.4)
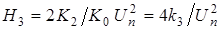, (4.5)
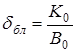, (4.6)
где 
– амплитуда полезного выходного сигнала;
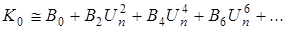(4.7)
– постоянная составляющая коэффициента усиления, определяемая как нулевая гармоника ряда Фурье;
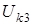– амплитуда комбинационной составляющей третьего порядка, изменяющаяся с частотой 
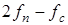или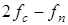 
; 
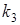– коэффициент интермодуляционных помех 3-го порядка;
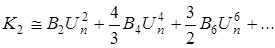– (4.8)
– вторая гармоника ряда Фурье, ответственная за образование комбинационных помех 3-го порядка;
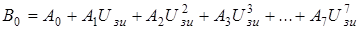– (4.9)
– полином, аппроксимирующий экспериментальную функцию, выражающую коэффициент усиления в рабочей точке усилителя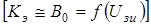 
.
; 
; 
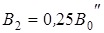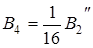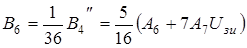– (4.10)
– вторые производные по напряжению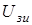 
от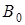 
, 
, 
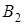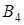, соответственно;
, 
, 
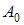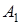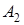и т.д. – коэффициенты усиления, их крутизна, кривизна и т.д. в рабочей точке, которые находятся как коэффициенты аппроксимирующего полинома;
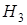– обобщенный параметр нелинейности третьего порядка, который в малосигнальном режиме (Uс << Uп) не зависит от входного сигнала, а определяется значением коэффициента усиления 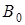и его производными в рабочей точке
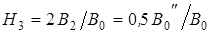(4.11)
Следовательно, параметр нелинейности 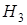, зависящий от второй производной малосигнального коэффициента усиления 
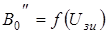в любой рабочей точке 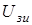, является определяющим в оценке нелинейных свойств усилителя по интермодуляции 3-го порядка. Чем более 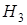стремится к нулю (т.е. 
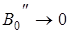), тем меньше коэффициент интермодуляции 3-го порядка 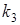, иначе тем более линейным является усилительный прибор (транзистор).
Коэффициент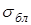 
в формуле (4.6), определяющий степень блокирования малого сигнала помехой большого уровня, как видно из формулы (4.7) в соответствующей рабочей точке зависит только от уровня помехи.
