Цель работы: научить рассчитывать параметры интегратора на основе интегрального ОУ.
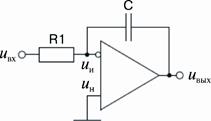Рис. 54
|
У интегратора форма выходного напряжения представляет собой интеграл от формы входного напряжения. Схема идеального интегратора на ОУ показана на рис. 54.
Согласно второму правилу ОУ i вх» i С. Ток конденсатора и напряжение на нем связаны соотношением
.
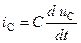Поскольку согласно рис. 54
,
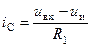получаем
.
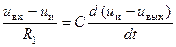Согласно правилу 1 и и» и н. Поскольку и н = 0, получаем
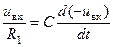, или 
.
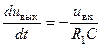Интегрируя обе части уравнения по времени, получаем
,
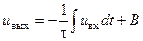где В – постоянная интегрирования, т. е. начальное напряжение на конденсаторе (U C0) в момент времени t = 0;
t = R 1 C – постоянная времени интегрирования.
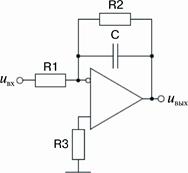Рис. 55
|
Таким образом, выходное напряжение интегратора (рис. 1) равно интегралу от входного напряжения и обратно пропорционально постоянной времени интегрирования.
Постоянное напряжение на выходе интегратора будет даже тогда, когда входное напряжение равно нулю. При отсутствии входного напряжения интегратор работает как усилитель без обратной связи, поскольку конденсатор препятствует протеканию тока от выхода к инверсному входу. Тем не менее, конденсатор все время заряжается малыми токами дрейфа и смещения, что приводит к усилению напряжения ошибки. Поэтому в схемах реальных интеграторов (рис. 55) параллельно конденсатору включают резистор (R2), который обеспечивает путь для протекания постоянного тока, что позволяет минимизировать напряжение ошибки. Кроме того, с помощью этого резистора ограничивается коэффициент усиления на низких частотах. Резистор R3 введен в схему для компенсации дрейфа ОУ.
Коэффициент передачи идеального интегратора (рис. 54) определяется как
,
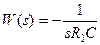т. е. он обратно пропорционален частоте (рис. 56).
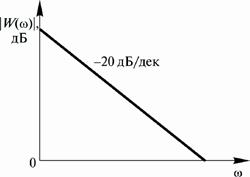Рис. 56
| 
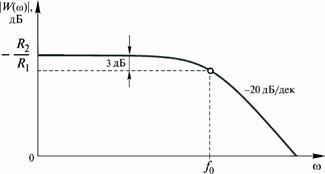Рис. 57
|
Для реального интегратора (рис. 56) коэффициент передачи имеет вид
.
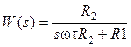ЛАХ реального интегратора показана на рис. 57.
В реальном интеграторе на частотах, при которых реактивное сопротивление конденсатора Х С сравнимо с сопротивлением R 2, общий импеданс обратной связи не будет преимущественно емкостным, что не даст точного интегрирования. В общем случае, точное интегрирование начинается на частотах, значительно превышающих частоту, при которой Х С = R 2. Таким образом, для точного интегрирования необходимо выполнение условия
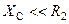, или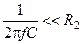 
,
откуда
.
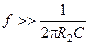Определим критическую частоту, при которой Х С = R 2
.
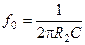Эта частота определяет частоту излома ЛАХ реального интегратора (рис. 57).
На частотах, меньших f 0, когда коэффициент усиления постоянен и равен (– R 2/ R 1), схема не работает как интегратор. На частотах, превышающих f 0, спад коэффициента усиления составляет 20 дБ/дек, т. е. схема работает как интегратор до частоты, при которой коэффициент передачи становится равным нулю.
Порядок расчета интегратора. Для расчета интегратора (рис. 55) необходимо задать:
† амплитуду входного напряжения (U вх max);
† частоту, с которой необходимо начать интегрировать входной сигнал (f);
† частоту (f 1), на которой амплитуда входного сигнала должна быть ослаблена до заданного уровня (Uf 1 max).
Расчет производится в следующем порядке.
² Выбираем емкость конденсатора С в диапазоне (0,01…1) мкФ.
² Выбираем критическую частоту f 0 на одну декаду ниже f.
² Находим сопротивление резистора R2
.
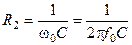² Определяем сопротивление резистора R1 таким, чтобы на частоте f 1
.
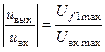На частоте f 1 (во много раз большей f 0) влиянием резистора R2 можно пренебречь. Поэтому в этом случае применимо выражение для определения коэффициента передачи идеального интегратора
,
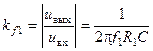откуда
.
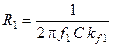Порядок выполнения работы
1. Получить задание на расчет интегратора– значения U вх max, f, f 1 и Uf 1 max.
2. Подобрать емкость конденсатора С в диапазоне (0.01...1 мкФ).
2. Рассчитать сопротивления резисторов R1 и R2. По результатам расчета построить ЛАХ и ФЧХ интегратора (рис. 55). Пример расчета с помощью программы MathCAD приведен на рис. 58.
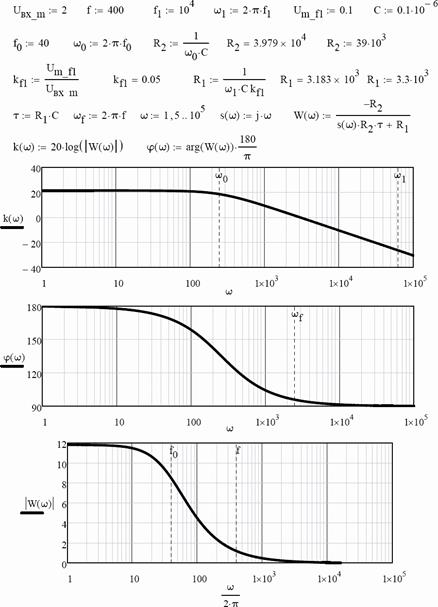
Рис. 58
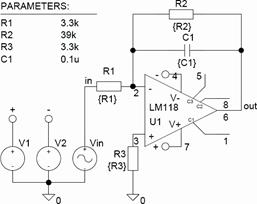Рис. 59
|
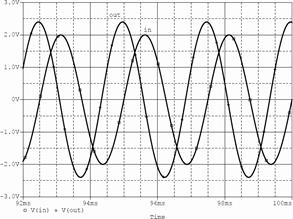
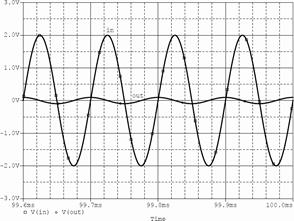
3. Проверить результаты расчета и функционирование интегратора с помощью моделирования. Схема модели интегратора показана на рис. 59. Результаты моделирования частотных характеристик приведены на рис. 60 (а – ЛАХ и ФЧХ; б – зависимость коэффициента усиления от частоты сигнала). Результаты моделирования при подаче на вход интегратора синусоидального напряжения показаны на рис. 61 (а – f = 400 Гц; б – f 1 = 10 кГц), а при подаче на вход прямоугольных импульсов – на рис. 62.
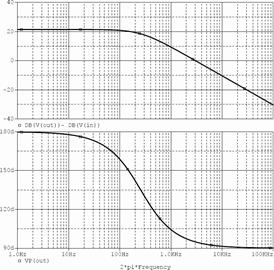а
| 
б
|
Рис. 60
а
| 
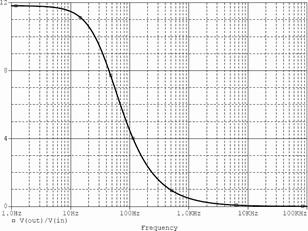б
|
Рис. 61
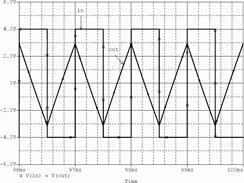Рис. 62
|
4. Собрать схему интегратора (рис. 63). Ко входу интегратора подключить генератор синусоидальных сигналов (ЗГ). Установить частоту ЗГ 20 Гц. Включить питание стенда. Установить на выходе интегратора напряжение максимальной амплитуды без искажений. Изменяя частоту ЗГ от 20 Гц до 220 кГц и поддерживая постоянной амплитуду входного напряжения (U вх), снять ЛАХ интегратора. Результаты занести в таблицу 5. Отключить питание стенда. По данным из таблицы 5 построить ЛАХ интегратора и зависимость и вых = j(f).
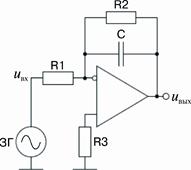Рис. 63
|
5. Установить частоту сигнала ЗГ, равной заданной. Включить питание стенда. Зарисовать осциллограммы входного и выходного напряжений интегратора. Отключить питание стенда.
6. Отключить от входа генератор синусоидального сигнала и подать на вход ФНЧ импульсное напряжение от стенда. Включить питание стенда. Зарисовать осциллограммы и вх(t) и и вых(t). Отключить питание стенда.
Таблица 5
| U вх, В | U вых, В | f, кГц | w, рад/с |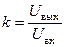 
| 20 lg(k) |
| 0,02 | |||||
| |||||
Содержание отчета
1. Схема исследуемого интегратора
2. Результаты вычислений и графики.
3. Таблица 1 и экспериментальная ЛАХ интегратора.
4. Осциллограммы по п. 5.
