Схема лабораторной установки представлена на рис. 6. Установка состоит из напорного 1 и приемного 2 баков. Расход жидкости, а следовательно, и скорость истечения струи регулируется с помощью задвижки 5. В напорном баке поддерживается постоянный уровень воды за счет подачи её из водопровода 8.
Порядок выполнения работы
Первый опыт
1. Установить на шайбе диск с круглым отверстием 5.
2. Открыть кран 9 подачи воды в напорный бак 1 и наполнить бак.
3. После наполнения напорного бака 1 и установления в нем постоянного напора Н, при котором происходит слив небольшого объема воды по трубе холостого сброса 7, открывают кран 4, и из отверстия вытекает струя, падающая по параболической траектории в мерный бак 3.
4. Записать величину напора Н по водомерному стеклу (пьезометру) 10.
5. Измерить горизонтальную проекцию струи x.
6. Записать вертикальную проекцию струи y.
7. Для подсчета расхода Q определяется объем воды, поступившей в мерный бак 3 за время t.
8. После снятия всех измерений закрыть кран 4.
Второй опыт
9. Установить диск с насадком Вентури. При напоре Н как в первом опыте выполнить пункты 5-7. Измерить вакуум в насадке Вентури с помощью жидкостного вакуумметра.
10. После снятия всех измерений закрыть кран 4.
Третий опыт
11. Установить диск с конически сходящимся насадком. При напоре Н как в первом опыте выполнить пункты 5-7.
12. После снятия всех измерений закрыть кран 4.
Четвертый опыт
13. Установить диск с конически расходящимся насадком. При напоре Н как в первом опыте выполнить пункты 5-7.
14. После снятия всех измерений закрыть кран 4 и 9.
15. Полученные данные поместить в таблицу и произвести необходимые расчеты. Привести пример расчета.
Таблица 1
Экспериментальные данные и обработка результатов
| Измеряемые и определяемые величины | Первый опыт | Второй опыт | Третий опыт | Четвертый опыт |
| круглое отверстие | насадок Вентури | конически сходящийся насадок | конически расходящийся насадок | |
| Действующий напор по пьезометру H, см | ||||
| Горизонтальная проекция струи х, см | ||||
| Вертикальная проекция y, см | ||||
| Объем воды V, см3 | ||||
| Время наполнения t, с | ||||
| Вакуумметрическая высота hвак, мм | – | – | – | |
| Диаметр выходного отверстия, мм | ||||
Площадь выходного отверстия, см 2
| ||||
Расход действительный, см3/с
| ||||
Коэффициент скорости φ
| ||||
Коэффициент расхода μ
| ||||
Коэффициент сжатия струи,
| ||||
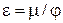
Коэффициент сопротивления ζ,
|
ЛАБОРАТОРНАЯ РАБОТА № 9
«ОПРЕДЕЛЕНИЕ ПОЛЕЙ СКОРОСТЕЙ В
ПЛОСКИХ ТУРБУЛЕНТНЫХ СТРУЯХ»
Цель работы:
1. Изучение поля скоростей в плоской турбулентной струе воздуха.
Краткая теория
Потоки жидкости или газа, не имеющие твердых границ, называются соответственно жидкими или газовыми струями.
Струя жидкости или газа называется свободной, если она не ограничена твердыми стенками. Струю считают затопленной, если она распространяется в пространстве, занятом жидкостью (капельной или газообразной), однородной данной. Например, затопленными струями являются: струя воды, выходящая из отверстия резервуара при истечении под «уровень»; струя воздуха, выходящая из отверстия замкнутого резервуара в атмосферу.
По форме поперечного сечения струи делят на осесимметричные (круглое сечение) или плоские.
Режим движения струй может быть ламинарным или турбулентным. В лабораторной работе будем рассматривать турбулентные струи как наиболее часто встречающиеся.
В турбулентной струе наблюдается беспорядочное движение вихревых масс. Эти массы при своем поперечном перемещении попадают за пределы струи, переносят в соприкасающиеся со струей слои неподвижной жидкости свои импульсы и увлекают эти слои. На место частиц, выброшенных из струи, в нее проникают частицы окружающей жидкости, которые подтормаживают граничные слои потока; устанавливается обмен вещества между струей и неподвижной жидкостью, в результате чего масса струи растет, ширина ее увеличивается, скорость у границ убывает.
Подторможенные частицы активного потока вместе с увеличенными частицами окружающей жидкости образуют турбулентный пограничный слой струи, толщина которого в направлении течения возрастает.
Рис. 1 Формирование пограничного слоя в свободной струе
Если в выходном сечении сопла скорости распределяются равномерно, то в начале струи толщина пограничного слоя равна нулю. В этом случае границы пограничного слоя представляют собой расходящиеся поверхности, которые пересекаются у кромки сопла (точка А, рис. 1).
С внешней стороны пограничный слой струи соприкасается с неподвижной жидкостью, причем, под внешней границей понимают поверхность, во всех точках которой составляющая скорости, параллельная оси струи, равна нулю (u=0).
С внутренней стороны пограничный слой переходит в ядро постоянных скоростей. Таким образом, на внутренней границе пограничного слоя скорость потока равна скорости истечения (u0).
Сечение струи, в котором завершается ликвидация ядра постоянной скорости, называют переходным сечением (рис. 2). Участок расположенной между срезом сопла и переходным сечением струи называют начальным, а участок, следующий за переходным, называют основным. Если принять угол расширения границ струи β одинаковым на основном и начальном участках (на самом деле они несколько отличаются) и продлить внешние границы основного участка, то найдем точку их пересечения – так называемый полюс струи (точка О).
Рис. 2. Строение свободной струи
Угол расширения характеризуется значениями 
, для плоских струй:
(1)
где а – коэффициент, характеризующий влияние турбулентности струй на ее расширение.
Давление по длине струи сохраняется постоянным и равным давлению в окружающем пространстве. Количество движения струи по длине также не изменяется.
На рис.3 показана эпюра скоростей в каком-либо поперечном сечении основного участка струи шириной 2b (где b – полуширина струи, см. рис. 2).
 |
Если на одном и том же чертеже в одном и том же масштабе построить эпюры скоростей для ряда поперечных сечений основного участка, то получим картину, представленную на рис. 4.
Одним из основных свойств струи является признак подобия скоростных полей в различных сечениях основного участка. Этот признак выражается в следующем: если эпюры скоростей построить в переменных 
и 
, то полученные эпюры скоростей во всех поперечных сечениях будут тождественны (подобны). Здесь принято:
umax – величина скорости на оси в рассматриваемом сечении;
u – любое (текущее) значение скорости в этом же сечении на расстоянии z от оси струи;
z0,5 – ордината частицы, обладающей скоростью, равной половине максимальной скорости (см. рис. 5).
На рис.6 точками обозначены значения безразмерных скоростей , взятые из различных сечений основного участка струи, отстоящих от среза сопла на расстоянии, соответствующих х 1, х 2, х 3.
Для определения величины скорости u, в какой-либо точке струи при ее истечении в атмосферу, воспользуемся уравнением Бернулли
(2)
рполн – полное давление в точке струи;
- динамическое давление, которому соответствует скоростной напор.
Выразив разность давлений 
через высоту вертикального столба жидкости в дифференциальном манометре, будем иметь
(3)
где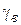 
- удельный вес воздуха;
gж-удельный вес жидкости (воды);
h - пьезометрический напор, соответствующий полному давлению;
h 0- пьезометрический напор, соответствующий атмосферному давлению.
Из выражения (3) записываем формулу для определения скорости воздуха в струе
(4)
В нашем случае g ж =1000 кг/м3, gв=11,6 кг/м3, тогда 
Выражая 
в миллиметрах, т.е. в тех единицах, в которых эту величину отсчитывают, получим скорость в метрах в секунду:
(5)
Расчетные соотношения для свободной затопленной плоской турбулентной струи приведены в табл. 1.
Таблица 1 – Расчетные соотношения для свободной затопленной плоской турбулентной струи
| Параметр | Значение параметра или расчетная формула для плоской струи |
| Коэффициент турбулентной структуры а | 0,09-0,12 |
| Половина угла расширения струи b | 2,4 а |
| Расстояние от полюса до начального сечения х 0, м |  ,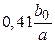
где b 0 – полуширина сопла, м
|
| Длина начального участка х н, м | 
|
| Полутолщина струи b, м |  ,
где хi – расстояние между начальным и рассматриваемым сечением, м
|
| Скорость на оси основного участка струи u max, м/с | 
|
| Расход истечения струи из сопла Q 0, м 3/ с |  ,
где l 0 – длина сопла, м
|
| Расход на основном участке Q, м 3/ с | 
|
ПОРЯДОК ПРОВЕДНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Включить установку в электрическую сеть, установив заданное преподавателем напряжение (100 В, 150 В, 210 В).
2. С помощью координатника установить трубку 1 в центре сопла (щели) и снять разность пьезометрических напоров D h 0 (разность напоров между трубкой 1 и трубкой Р).
3. По формуле (4) определить скорость u0.
4. Установить координатник с трубками на расстоянии х 1 от среза сопла (щели) и промерить все поперечное сечение струи с шагом 1 мм, записывая разность пьезометрических напоров D h в таблицу 2.
5. Тоже самое проделать на расстоянии х 2, х 3 от среза сопла (щели).
6. Составить таблицу для экспериментальных и расчетных данных характеристик струи.
7. Построить графики для экспериментальных данных, аналогичные рисункам 5 и 6. Для этого по формуле (4) рассчитываем все скорости по сечению струи. Строим график №1 
Для того чтобы построить график аналогичный рис. 6, необходимо перейти к безразмерным параметрам. Поэтому находим отношение , затем по графику находим значение z0,5 соответствующее значению 
и берем отношение 
.
Строим график №2 по данным значениям скоростей в каждом из рассмотренных сечений, наносятся на график условными обозначениями (для сечения, отстоящего от среза сопла (щели) на расстоянии х 1 - o, х 2 - à, х 3 - *.
8.Сделать выводы по построенным графикам.
Размеры сопла: длина сопла l 0= 0,075 м; полуширина сопла b 0=0,00025 м
Таблица 2 – Таблица для экспериментальных и расчетных данных характеристик струи
 Напряжение, В
| Разность пьезометрических напоров D h 0, мм, измеренная в центре сопла | Скорость u0, м/с, в центре сопла | Расстояние z, мм, от оси струи в поперечном направлении | Разность пьезометрических напоров D h, мм, на расстоянии | Скорость u, м/с, в данной точке струи на расстоянии | Скорость на оси основного участка струи u max, м/с |
|
| Расчетные значения | ||||||||||||||||
| х1 = | х2 = | х3 = | х1 | х2 | х3 | х1 | х2 | х3 | х1 | х2 | х3 | х1, z0,5= | х2, z0,5= | х3, z0,5= | Скорость на оси основного участка струи u max, м/с | Расход истечения струи из сопла Q 0, м 3/ с | Расход на основном участке Q, м 3/ с | ||||||||
| х1 | х2 | х3 | х1 | х2 | х3 | ||||||||||||||||||||
| 
| По графику №1 | z0,5 находим по графику №1 | По таблице 1 | По таблице 1 | По таблице 1 | |||||||||||||||||||
ЛАБОРАТОРНАЯ РАБОТА № 11
«ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ФИЛЬТРАЦИИ
ПЕСЧАНОГО ГРУНТА»
Цель работы:
1. Определить экспериментальным путем коэффициента фильтрации песчаного грунта с помощью прибора Дарси.
Краткая теория
Движение жидкости или газа через пористую среду называется фильтрацией. Изучение вопросов фильтрации представляет большой практический интерес для решения широкого круга инженерных задач в различных областях техники: водоснабжении – для расчета притока воды к колодцам и дренам; гидротехническом и мелиоративном строительстве – для расчета расходов и уровней грунтовых вод при орошении и осушении почв, строительстве плотин, устройстве котлованов и т. д.
Если жидкость при фильтрации образует свободную поверхность в грунте (например, в плотине), то такую фильтрацию называют безнапорной.
Напорная фильтрация имеет место в напорных водоносных горизонтах, где движение жидкости происходит за счет разности давлений в пласте и скважине без образования свободной поверхности. Фильтрация может быть также ламинарной и турбулентной, установившейся и неустановившейся.
А. Дарси исследовал фильтрацию воды на опытной установке, представляющей собой вертикальный сосуд постоянного сечения, заполненный песком. Через песок пропускалась вода при постоянной разности напоров. Толщина слоя песка, его фракционный состав и разность напоров в разных опытах были различны.
Было экспериментально установлено, что зависимость расхода от потерь напора имеет следующий вид:
,
где k – коэффициент фильтрации жидкости; ω – «геометрическая» площадь поперечного сечения образца грунта, включающая площадь пор ωпор и площадь частиц ωчаст (ω=ωпор+ωчаст); J – гидравлический уклон, представляющий собой отношение потерь напора h тр на пути фильтрации к длине этого пути l: 
.
Средняя скорость фильтрации υ по закону Дарси
.
Это условная скорость фильтрации, так как в практических задачах принимается, что фильтрация происходит через все сечение грунта, включая твердые частицы.
Фильтрация жидкости в каждом сечении происходит только через площадь пор ωпор, поэтому истинная скорость фильтрации υд равна
.
Истинная скорость фильтрации υд всегда больше скорости фильтрации υ, и их взаимосвязь устанавливается зависимостью
,
где m – коэффициент пористости, численно равный отношению объема пор в породе W п ко всему объему W, т. е. 
.
Коэффициент фильтрации k зависит от величины и формы зерен грунта, наличия глинистых частиц, плотности и вязкости фильтрующей жидкости и её температуры.
Закон Дарси справедлив для ламинарного движения, которое широко распространено в природных условиях.
При турбулентном режиме движения наблюдается отклонение от линейного закона. Здесь скорость фильтрации прямо пропорциональна гидравлическому уклону в степени ½.
Скорость фильтрации, при которой происходит нарушение закона Дарси, называют критической скоростью и обозначают υкр. Её значение можно определить экспериментально по графику υ = f (J) в точке его заметного отклонения от прямой линии. Следовательно, опыты проводят до тех пор, пока прямая не перейдет в кривую.
Коэффициент фильтрации грунта может быть определен:
1) лабораторным путем с помощью приборов Дарси, Каменского, Тиме, Капецкого;
2) в полевых условиях в естественном состоянии грунта;
3) расчетным методом по данным гранулометрического состава с помощью расчетных формул.
Из-за того, что эмпирические расчетные формулы имеют узкие пределы применимости, их использование нецелесообразно, тем более что имеются достаточно простые приборы для непосредственного определения коэффициента фильтрации.
