Вода в трубопровод (рис. 4) поступает из напорного бака и, пройдя по трубопроводу с установленными на нем местными сопротивлениями 6, 7. 8, 9 сливается в мерный бак 5. Пьезометрические напоры до и после местных сопротивлений измеряются пьезометрами, установленными на пьезометрическом щите. С помощью крана 4, можно регулировать расход и, следовательно, скорость движения жидкости в трубопроводе.
Рис. 4. Схема лабораторной установки
|
Порядок проведения работы
1. Полностью открыть кран 3.
2. Открыть кран 4 с таким расчетом, чтобы мениски жидкости в пьезометрах оставались в пределах стеклянных трубок.
3. Не изменяя положение крана 4 с помощью секундомера определить время t наполнения слоя воды с в мерном баке 5.
4. Не изменяя положение крана 4 измерить перепад уровней жидкости 
(потерянный пьезометрический напор) в пьезометрах до и после местного сопративления.
5. Изменяя степень открытия крана 4, повторить экспериментальное наблюдение трижды.
6. Закончив опыты, слить воду из мерного бака 5, закрыть кран 4.
Обработка опытных данных
1. Определить объем воды V, см 3, заполнения мерного бака. Размеры мерного бака: а =19 см, b =44 см.
.
2. Определить расход Q,зная время t, с, заполнения объема воды V в мерном баке по формуле:
.
3. Определить скорость движения воды в трубах
,
где 
– площадь поперечного сечения трубы, d 1=33 мм.
4. Для каждого замера определить значение коэффициентов местных сопротивлений 
по формуле:
,
где – потери напора на соответствующих местных сопротивлениях;
– средняя скорость потока 
;
– площадь поперечного сечения потока;
– ускорение свободного падения, см/с2.
5. Определить значение числа Рейнольдса
,
где ν – кинематический коэффициент вязкости воды, 
.
6. Для опытов при которых Re>104 cравнить полученные результаты для 
с теоретическим 
, полученные значения z в.с. с теоретическим 
. Для внезапного сужения построить график зависимости 
.
7. Данные свести в табл. 1.
Таблица 1
Экспериментальная таблица
| Измеряемые и искомые величины | Единицы измерения | Вид сопротивления | |||||||||
| вентиль | плавный поворот | внезапное расширение | внезапное сужение | ||||||||
| Номер опыта | |||||||||||
| Высота слоя воды, с | см | ||||||||||
| Объем жидкости, V | см3 | ||||||||||
| Время наполнения объема, t | с | ||||||||||
Расход,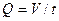 
| см3/с | ||||||||||
Скорость, 
| см/с | ||||||||||
Разность уровней, 
| см | ||||||||||
| Диаметр, d 1 | см | 3,3 | |||||||||
| Диаметр, d 2 | см | 6,0 | |||||||||
Площадь, 
| см2 | ||||||||||
Площадь,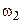 
| см2 | ||||||||||
Коэффициент z м.с (экспериментальные значения), 
| – | ||||||||||
| Теоретическое значение .
| – | – | – | – | – | – | – | – | – | ||
| Теоретическое значение
| – | – | – | – | |||||||
ЛАБОРАТОРНАЯ РАБОТА № 6
«ПОСТРОЕНИЕ ДИАГРАММЫ УРАВНЕНИЯ БЕРНУЛЛИ»
Цель работы
Изучение различных составляющих удельной энергии потока при движении жидкости по трубопроводу переменного сечения и направления и характера изменения энергии потока по его длине.
Вводная часть
Если в потоке несжимаемой жидкости действуют из массовых сил только силы тяжести, то выражение полной удельной энергии в любой точке можно представить в следующих трех вариантах:
, (1)
, (2)
, (3)
где z – превышение рассматриваемой точки над выбранной плоскостью отсчета (сравнения);
р, и – соответственно гидростатическое давление и скорость движения жидкости в этой точке.
Формула (1) выражает, энергию, приходящуюся yа единицу веса (м), (2) – на единицу объема (Па), (3) – на единицу массы жидкости (м2/с2).
В гидравлике широко применяется запись (1). Три составляющие правой части этого уравнения имеют следующий физический смысл:
z – удельная потенциальная энергия положения точки над плоскостью сравнения;
– удельная потенциальная энергия давления жидкости в точке (пьезометрический напор);
– удельная кинетическая энергия (скоростной напор).
Уравнение Бернулли выражает закон сохранения энергии в потоке жидкости. Оно устанавливает связь между удельными энергиями в двух любых сечениях потока. Если использовать запись (1) применительно не к точкам, а к сечениям потока, то уравнение Бернулли представляется в следующем виде:
, (4)
где u1, u2 – средние скорости движения жидкости в первом и втором сечениях потока;
a1, a2 – коэффициенты кинетической энергии в этих сечениях;
hтp – потери энергии при движении жидкости от первого сечения ко второму.
Полная удельная энергия в первом сечении потока отличается от полной удельной энергии во втором сечении на величину потерь hтp.
При изменении положения и площади сечения потока происходит преобразование одного вида энергии в другой. Уравнение (4) позволяет находить одну из неизвестных составляющих полной удельной энергии, если известны все остальные.
Уравнение Бернулли можно изобразить на графике, называемом диаграммой уравнения Бернулли.
Для построения диаграммы уравнения Бернулли от произвольно выбранной плоскости сравнения 0-0 (рис. 1) откладываем вверх z (ординаты). От ординаты z откладываем вверх значения пьезометрического напора 
и получаем линию b’-c’-d’-f’-h’, называемую пьезометрической линией. Откладывая далее вверх от пьезометрической линии значения скоростного напора 
, получаем линию гидравлического напора а-b-c-d-f-h, расстояние от которой до плоскости сравнения 0-0 дает значение гидродинамического напора (полной удельной энергии) в соответствующих сечениях струйки.
