Определение 10.1. Любойсвязный неорграф, не содержащий циклов, называется(неориентированным) деревом.
Определение 10.2. Любой неорграф без циклов называется лесом, или ациклическим графом.
Таким образом, компонентами связности любого леса являются деревья.
На рис. 17 показан лес, состоящий из двух деревьев.
Свойства деревьев сформулируем в виде следующей теоремы.
Теорема 10.1. Пусть G = (S, U) и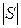 
= n, 
= m. Тогда следующие условия эквивалентны:
1) G – дерево;
2) G – связный граф и m = n - 1;
3) G – ациклический граф и m = n - 1;
4) любые две различные вершины графа соединяет единственная простая цепь;
5) G – ациклический граф, такой, что если какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
Теорема 10.2 (Кэли). Число деревьев с n занумерованными вершинами равно 
.
Определение 10.3. Ориентированным деревом (ордеревом) называется
орграф G = (S, U), удовлетворяющий следующим двум условиям:
1) существует единственная вершина xiÎ S, называемая корнем, не имеющая предшествующих вершин (т. е. 
);
2) любой вершине xj, отличной от xi, в орграфе G непосредственно предшествует ровно одна вершина (т. е. 
).
Определение 10.4. У злом ордерева называется вершина, отличная от корня.
Определение 10.5. Л истом ордерева называется вершина x такая, что 
и 
Определение 10.6. Ветвью ордерева называется путь из корня в лист.
Определение 10.7. Высотой ордерева называется длина его наибольшей ветви.
Определение 10.8. Уровнем вершины ордерева называется расстояние от корня до этой вершины.
Отметим, что корень имеет уровень 0.
Определение 10.9. Ярусом ордерева называется множество вершин одного уровня.
Замечание 10.1. Неориентированное дерево можно преобразовать в ориентированное, выбрав в качестве корня произвольную вершину. На рис. 18 корень графа – вершина x7.
Пример 10.1. Рассмотрим ордерево, изображëнное на рис. 18. Тогда: все вершины, кроме x7, являются узлами ордерева; вершины x1, x5, x8, x10, x11, x12 – листами; путь x7 ® x6 ® x3 ® x2 ® x10 – одна из ветвей; высота ордерева равна 5; множество вершин { x1, x5, x9, x10 } уровня 4 образует один из ярусов ордерева.
Определение 10.10. Остовом неорграфа G = (S, U) называется его часть G¢ = (S¢, U¢), такая, что S¢ = S и G¢ – лес, образующий дерево на любой связной компоненте графа G.
Из определения 10.10 следует, что если G – связный неорграф, то остов G¢ является деревом, которое будем называть остовным деревом графа G.
Определение 10.11. Остовом орграфа G называется его часть G¢, такая, что ассоциированный с G¢ неорграф F(G¢) является остовом графа F(G).
Понятие остовного дерева для связного орграфа вводится аналогично.
Замечание 10.2. 1) В каждом графе существует остов, который можно получить, разрушая в каждой связной компоненте циклы, т.е. удаляя лишние рëбра.
2) Остов графа определяется неоднозначно.
Пример 10.2. На рис. 19 изображены неорграф G и один из его остовов G¢.
Для подсчета числа остовов в неорграфе используется матрица Кирхгофа.
Теорема 10.3 (Кирхгофа). Число остовных деревьев в связном неорграфе G порядка n ³ 2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа.
Из определения дерева вытекает следующая теорема.
Теорема 10.4. Пусть G = (S, U) – произвольный неорграф, 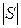= n, = m, k – число компонент связности графа G. Число рëбер, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно m – n + k.
Доказательство. Пусть i -я компонента связности Gi содержит ni вершин и mi рëбер. По условию G – связный граф. Следовательно, остов Gi ¢ графа Gi является деревом, а значит, он содержит (ni – 1) ребро. Таким образом, для получения остова Gi ¢ из i -й компоненты связности Gi требуется удалить mi – (ni – 1) ребер.
Просуммируем удаляемые ребра по всем компонентам связности, учитывая, что 
Получим 
Определение 10.12. Число n (G) = m - n + k называется цикломатическим числом или циклическим рангом графа G.
Определение 10.13. Число n* (G) = n - k называется коциклическим рангом или корангом.
Таким образом, n * (G) равно числу рëбер, входящих в любой остов графа G. Очевидно, что n (G) +n* (G) = m.
Из теоремы 10.4 непосредственно вытекают два следствия.
Следствие 10.4.1. Неорграф G является лесом тогда и только тогда, когда
n (G) =0.
Следствие 10.4.2. Неорграф G имеет единственный цикл тогда и только тогда, когда n (G) =1.
Пример 10.3. Найти для графа G, изображенного на рис. 19, цикломатическое число и коциклический ранг.
Решение. Граф G имеет 8 вершин, 14 ребер и 1 компоненту связности. Тогда, согласно по теореме 10.4, цикломатическое число n (G) = 14 – 8 +1 = 7, а коциклический рангn * (G) = 8 – 1 = 7.
Эйлеровы цепи и циклы
Пусть G – псевдограф.
Определение 11.1. Цепь (цикл) в G называется эйлеровым (эйлеровой), если она (он) проходит по одному разу через каждое ребро псевдографа G.
Определение 11.2. Псевдограф G называется эйлеровым, если он содержит эйлеров цикл.
Заметим, что эйлеров псевдограф можно нарисовать, не отрывая карандаша от бумаги и не повторяя линий.
Теорема 11.1. Для того чтобы связный псевдограф обладал эйлеровым циклом, необходимо и достаточно, чтобы степени его вершин были чëтными.
Теорема 11.2. Для того чтобы связный псевдограф обладал эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно две вершины нечëтной степени.
Таким образом, мы имеем легко проверяемые необходимые и достаточные условия существования в произвольном связном псевдографе эйлерова цикла или эйлеровой цепи.
Пример 11.1 (решение задачи о кëнигсбергских мостах). Поставим в соответствие схеме центральной части города Кëнигсберг, приведëнной на
рис. 1, мультиграф G, изображëнный на рис. 20, в котором каждой части суши соответствует вершина, а каждому мосту – ребро, соединяющее соответствующие вершины. На языке теории графов задача формулируется следующим образом: найти эйлеров цикл в мультиграфе G.
Воспользуемся теоремой 11.1. Заметим, что для мультиграфа G, изображëнного на рис. 20, имеем
deg (x1) = 5, deg (x2) = deg (x3) = deg (x4) = 3, т.е. необходимое и достаточное условие существование эйлерова цикла не выполняется, следовательно, мультиграф G не обладает эйлеровым циклом.
Гамильтоновы цепи и циклы
В 1857 году математик Гамильтон придумал игру «Кругосветное путешествие». Она включала додекаэдр (правильный многогранник), двенадцать граней которого представляли собой равные правильные пятиугольники. В каждой из двадцати вершин тела просверливалась дырка, в которую вставлялся колышек, изображавший город (столицу). Используя верëвку, требовалось найти путь через города, посетив каждый город один раз, и вернуться в исходный город. Додекаэдр на плоскости изображается так, как показано на рис. 21.
На языке теории графов задача сводится к нахождению в псевдографе простого цикла, проходящего через каждую вершину. Отсюда любой цикл псевдографа, обладающий таким свойством, называется гамильтоновым циклом.
Определение 12.1. Простая цепь (цикл) в псевдографе G называется гамильтоновой (гамильтоновым), если она (он) проходит через каждую вершину псевдографа G.
Рис. 21 Определение 12.2. Псевдограф, у которого есть гамильто-
нов цикл, называется гамильтоновым графом.
Очевидно, вопросы существования гамильтоновых цепей и циклов в псевдографах сводятся к аналогичным вопросам для простых графов. Следует отметить, что до сих пор неизвестны необходимые и достаточные условия существования в произвольном простом графе гамильтонова цикла или гамильтоновой цепи.
Однако имеется класс графов, в которых заведомо существуют гамильтоновы цепи и циклы – это полные графы. Таким образом, полнота графа является простейшим достаточным условием существования гамильтоновых цепей и циклов в простом графе.
Очевидным простейшим необходимым условием существования гамильтоновых цепей и циклов в простом графе является его связность. Более тонким необходимым условием существования гамильтоновых цепей и циклов в простом графе является отсутствие в нëм точек сочленения, т.е. вершин, удаление которых увеличивает число компонент связности.
Планарные графы
В замечании 3.1 отмечалось, что граф с точностью до изоморфизма можно изобразить разными диаграммами. На практике при изготовлении микросхем возникает задача изображения схемы радиоэлектронного устройства, представляющей собой граф, на плоскости так, чтобы проводники не пересекались. Аналогичная задача возникает при проектировании железнодорожных и других путей, где нежелательны переезды.
Таким образом, возникает потребность введения понятия плоского графа.
Определение 13.1. Плоским называется граф, вершины которого являются точками плоскости, а рëбра – непрерывными плоскими линиями без самопересечений, причëм никакие два ребра не имеют общих точек, кроме, быть может, инцидентной им обоим вершины.
Определение 13.2. Планарным называется любой граф, изоморфный плоскому графу.
Все планарныеграфы укладываются на плоскости (имеют плоскую укладку).
Пример 13.1. На рис. 22 изображëн планарный граф G и изоморфный ему плоский граф 
(плоская укладка графа G).
Очевидно, что следующие утверждения справедливы:
1) любой подграф планарного графа планарен;
2) граф планарен тогда и только тогда, когда каждая связная компонента этого графа является планарным графом.
Определение 13.3. Гранью плоского графаназывается множество точек плоскости, каждая пара которых может быть соединена плоской кривой, не пересекающей рëбер этого графа.
Определение 13.4. Границей грани плоского графаназывается множество вершин и рëбер, принадлежащих этой грани.
Пример 13.2. Плоский граф на рис. 22 имеет пять граней: Г1, Г2, Г3, Г4, Г5. Неограниченная грань Г1 называется внешней, а остальные грани: Г2, Г3, Г4, Г5 – внутренними.
Теорема 13.1 (Эйлера). Пусть G = (S, U) – связный планарный граф порядка n и 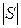= n, = m, f – число граней плоского графа. Тогда справедливо равенство
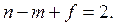(13.1)
Доказательство. Пусть G ¢ – некоторый остов графа G. Он имеет всего одну внешнюю грань, n вершин и (n – 1) ребер, поэтому формула (13.1) для остова
G ¢ выполняется. Будем поочерëдно добавлять к остову G ¢ недостающие ребра графа G. При каждом добавлении число вершин не изменится, число ребер и число граней увеличится на единицу.
Таким образом, формула (13.1) будет верна для всякого графа, получающегося в результате таких операций, а поскольку графом G заканчивается вся эта процедура, то формула (13.1) будет верна и для него.
Известны несколько критериев планарности графа. Для формулировки одного из них введëм понятие гомеоморфизма графов.
Определение 13.5. Два графа называются гомеоморфными, если они могут быть получены из одного и того же графа подразбиением его рëбер.
На рис. 23 изображëн исходный граф G и два гомеоморфных графа G1 и G2.
Теорема 13.2 (Понтрягина – Куратовского). Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K5 или K3,3.
Следующая теорема представляет собой эквивалентную формулировку критерия планарности 13.2.
Теорема 13.3. Граф планарен тогда и только тогда, когда в нëм нет подграфов, стягиваемых к графам K5 или K3,3.
Для непланарных графов вводятся характеристики, представляющие ту или иную меру непланарности.
Определение 13.6. Искажëнностью sk (G)графа G или числом планарности называется наименьшее число рëбер, удаление которых приводит к планарному графу.
Для полного графа порядка n справедлива следующая формула:
(13.2)
Определение 13.7. Толщиной t (G) графа G называется наименьшее число планарных подграфов графа G, объединение которых даëт сам граф.
Толщина графа равна минимальному числу плоскостей k, при котором граф G разбивается на плоские части G1, G2,…, Gk.
Очевидно, что толщина планарного графа равна единице. Для полного графа порядка n справедлива следующая формула:
t (Kn) = 
(13.3)
