Связность. Компоненты связности

Введение в теорию графов

Рекомендовано редакционно-издательским советом университета

в качестве учебно-методического пособия

 

Кострома

КГТУ

УДК 519.1 (075)

 

Чередникова, А.В. Введение в теорию графов / А.В. Чередникова,

И.В. Землякова. – Кострома: Изд-во Костром. гос. технол. ун-та, 2012. – 25 с.

В пособии рассматриваются основные понятия теории графов. Доступность изложения, сочетание теоретического материала с иллюстрирующими его примерами дают возможность студентам использовать пособие для самостоятельной работы при изучении дисциплины «Дискретная математика».

Пособие предназначено для студентов 1 курса бакалавриата по направлению подготовки 090900 «Информационная безопасность» и студентов 2 курса бакалавриата по направлениям подготовки 230100 «Информатика и вычислительная техника», 230400 «Информационные системы и технологии».

Пособие может быть также использовано при обучении математическим дисциплинам студентов бакалавриата всех направлений подготовки, государственные образовательные стандарты которых включают изучение и применение теории графов.

 

 

Рецензент: В.Н. Шведенко, д-р техн. наук, профессор,

зав. кафедрой информационных технологий КГТУ

© Костромской государственный технологический университет, 2012

ОГЛАВЛЕНИЕ

Введение. 4

§1. Основные понятия и определения. 4

§2. Способы задания графов. 7

§3. Изоморфные графы.. 9

§4. Взвешенные графы.. 10

§5. Подграф. 10

§6. Операции над графами. 12

§7. Маршруты, цепи, циклы.. 13

§8. Связность. Компоненты связности. 14

§9. Метрические характеристики графа. 17

§10. Деревья и их свойства. Лес. 18

§11. Эйлеровы цепи и циклы.. 20

§12. Гамильтоновы цепи и циклы.. 21

§13. Планарные графы.. 22

§14. Раскраска графов. Хроматические графы.. 24

Список литературы.. 25

 

 

Введение

Теория графов является одним из разделов дискретной математики, который исследует свойства конечных или счетных множеств с заданными отношениями между их элементами. Особенностью этой теории является геометрический подход к изучению объектов.

Впервые понятие «граф» ввёл в 1936 году венгерский математик Денеш Кëниг. Однако первая работа по теории графов была написана еще в 1736 году ЛеонардомЭйлером, в которой он решил «задачу о кëнигсбергских мостах». Суть этой задачи состоит в следующем. На рис. 1 представлена схема центральной части города Кëнигсберг (ныне Калининград), которая включает два берега реки, два острова в ней и семь соединяющих их мостов. Требуется обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку. Позже мы рассмотрим решение этой задачи.

Современная теория графов даёт исключительно удобный аппарат для моделирования структурных свойств различных систем и отношений между объектами разной природы. Поэтому она широко используется как в самой математике, так и еë приложениях в самых разнообразных областях науки, техники и практической деятельности. В частности, теория графов находит своë применение в информатике и программировании, химии, экономике, логистике, в коммуникационных и транспортных системах, схемотехнике.

Следует отметить, что для понятия «граф» нет общепризнанного единого определения. Разные авторы подразумевают под «графом» различные объекты, хотя и очень похожие. В данном пособии рассматриваются только конечные графы и используется терминология [5], позволяющая на множестве всех графов ввести бинарное отношение «быть частным случаем».

 

Основные понятия и определения

Пусть S – непустое конечное множество, V⁽²⁾ – множество всех его двухэлементных подмножеств.

Определение 1.1. Псевдографом (или просто графом) G называется пара множеств (S, U), где U – произвольное подмножество множества V⁽²⁾. При этом пишут G = (S, U).

Определение 1.2. Пусть G = (S, U) – псевдограф. Элементы множества S называются вершинами графа G, а элементы множества U – его рëбрами.

Определение 1.3. Граф G = (S, U) называется пустым или нуль-графом, если

U = Æ.

Определение 1.4. Число вершин графа G = (S, U) называется его порядком.

Если порядок графа равен n, то пишут 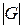= n.

Двухэлементное подмножество множества S (ребро), принадлежащее U и состоящее из элементов x и y, будем обозначать через (x, y).

В общем случае множество U может содержать пары с одинаковыми элементами вида (x, x) и одинаковые пары.

Определение 1.5. Рëбра вида(x, x) называются петлями.

Определение 1.6. Одинаковые пары из множества U называются кратными (или параллельными) рëбрами.

Таким образом, псевдограф может содержать петли и кратные рëбра. В этом смысле псевдографы еще называются графами с кратными рëбрами и петлями.

Определение 1.7. Псевдограф без петель называется мультиграфом (или графом с кратными рëбрами).

Определение 1.8. Мультиграф без кратных рëбер называется простым графом.

Таким образом, простой граф не содержит петель и кратных рëбер.

Графы имеют наглядную графическую интерпретацию в виде диаграмм, состоящих из точек и линий, соединяющих некоторые из этих точек. Точки соответствуют вершинам графа, а линии – его рëбрам. При этом форма и длина линий значения не имеют. Важно лишь, что две данные точки соединены или не соединены линией.

Пример 1.1. Указать, какие из графов, диаграммы которых изображены на

рис. 2, являются псевдографами, мультиграфами, простыми графами.

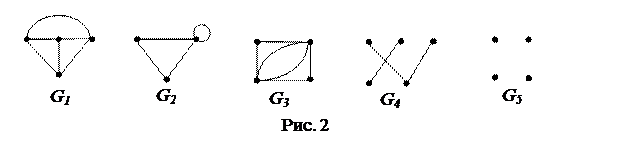
Решение. Все графы являются псевдографами, графы G₁, G₃, G₄, G₅ – мультиграфами, графы G₁, G₄, G₅ – простыми графами. 

Определение 1.9. Граф называется неориентированным (кратко – неорграфом), если пары в множестве U являются неупорядоченными.

Если (x, y) – неупорядоченная пара, то ребро (x, y) называется неориентированным, а вершины x и y называются концами неориентированного ребра

(x, y).

Определение 1.10. Граф называется ориентированным (кратко – орграфом), если пары в множестве U являются упорядоченными.

Определение 1.11. Ребра орграфа называются дугами (или ориентированными ребрами).

Вершина x дуги (x, y) называется еë началом, а вершина y – еë концом. В этом случае говорят, что дуга (x, y) исходит из вершины x и входит в вершину y.

На диаграммах орграфов направления дуг отмечаются стрелками, которые примыкают к их концам.

Замечание 1.1. Неориентированное ребро (x, y) равносильно двум противоположно направленным дугам (x, y) и (y, x). Поэтому неорграф можно рассматривать как орграф, который вместе с каждой дугой (x, y) содержит и дугу (y, x) противоположного направления. 

Условимся вершины графа обозначать буквами x, y, z (без индексов или с индексами), а ребра и дуги – буквами v, u, w (без индексов или с индексами).

Рассмотрим ряд понятий и определений для неор- и орграфов. При этом, если не будет оговорено особо, те же понятия и определения переносятся без изменений на неориентированные и ориентированные псевдографы.

Определение 1.12. Два ребра графа называются смежными, если они имеют общий конец.

Определение 1.13. Вершина x и ребро u графа называются инцидентными, если x является концом ребра u, и неинцидентными в противном случае.

Определение 1.14. Две вершины графа называются смежными, если существует инцидентное им ребро.

Определение 1.15. Число рëбер (дуг) графа (орграфа) G, инцидентных данной вершине x_i называется степенью (валентностью) вершины x_i и обозначается через deg (x_i) (от англ. degree – степень).

Определение 1.16. Вершина графа называется изолированной, если еë степень равна нулю.

Определение 1.17. Вершина графа называется висячей, если еë степень равна единице.

Замечание 1.2. В случае неориентированного псевдографа обычно считается, что вклад каждой петли, инцидентной некоторой вершине x, в еë степень P (x) равен 2, в то время как вклад любого другого ребра, инцидентного вершине x, равен 1. 

Определение 1.18. Полустепенью исхода (захода) вершины x_i орграфа называется число deg ⁺ (x_i) (deg ^– (x_i)) его дуг, исходящих из вершины x_i (заходящих в вершину x_i).

Для орграфа deg (x_i) = deg ⁺ (x_i) + deg ^– (x_i).

Замечание 1.3. В случае ориентированного псевдографа вклад каждой петли, инцидентной некоторой вершине x, равен 1, как в deg ⁺ (x), так и в deg ^– (x). 

Пример 1.2. Найти степени вершин x₂, x₄ графа G₁ и полустепени исхода и захода вершин x₂, x₄ графа G₂, изображëнных на рис. 3.

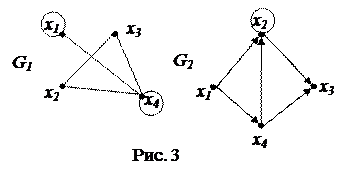Решение. Для графа G₁ имеем:

deg (x₂) = 2и deg (x₄) = 5.

Для графа G₂ имеем:

deg ⁺ (x₂) = 2, deg ^– (x₂) = 3 и

deg ⁺ (x₄) = 2, deg ^– (x₄) = 1. 

Определение 1.19. Неориентированный простой граф, в котором любые две различные вершины смежны, называется полным. Полный граф порядка n обозначается через K_n.

На рис. 4 изображены диаграммы полных графов K₁, K₂, K₃ и K₄.

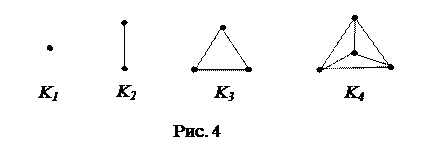
Определение 1.20. Неорграф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям.

Определение 1.21. Двудольный граф, любые две вершины которого, входящие в разные доли, смежны, называется полным двудольным. Полный двудольный граф, доли которого состоят из p и q вершин, обозначается символом K_p,q.

На рис. 5 изображены полные двудольные графы K_1,4 и K_3,3.

 

Способы задания графов

1. Перечислением (списком) вершин и рëбер (дуг).

2. Геометрическим способом. Граф может быть задан с помощью его диаграммы.

Пример 2.1. Пусть граф G = (S, U) задан списком вершин и рëбер:

S = { x₁, x₂, x₃, x₄, x₅, x₆ },

U = {(x₁, x₂),(x₁, x₃),(x₁, x₆),(x₂, x₃),(x₂, x₅),(x₃, x₄),(x₃, x₅), (x₃, x₆), (x₄, x₅)}. Тогда граф можно задать с помощью диаграммы, представленной на рис. 6. 

3. Матричным способом. Этот способ заданияиспользуется наиболее часто. Рассмотрим задание графа матрицей смежности вершин, матрицей смежности дуг, матрицей инциденций и матрицей Кирхгофа.

Определение 2.1. Матрицей смежности вершин графа G = (S, U) порядка n называется квадратная матрица P (G)= 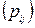порядка n, строки и столбцы которой соответствуют вершинам графа, где элементы p_ij равны числу дуг, идущих из i -й вершины в j -ю.

Для неорграфа матрица смежности вершин является симметричной относительно главной диагонали (см. замечание 1.1).

Определение 2.2. Матрицей смежности дуг графа G = (S, U), где = m, называется квадратная матрица Q (G)= 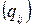порядка m, элементы q_ij которой равны единице, если дуга u_i непосредственно предшествует дуге u_j, и равны нулю в остальных случаях.

В случае неорграфа элемент q_ij равен единице, если u_i и u_j смежны, и нулю, если эти дуги не смежны.

Определение 2.3. Матрицей инциденций мультиграфа G = (S, U), где 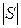= n и = m, называется прямоугольная матрица R (G)= размерности n ´ m. Элементы r_ij этой матрицы равны 1, если дуга u_j исходит из i -й вершины; –1, если дуга u_j входит в i -ю вершину; 0, если дуга u_j не инцидентна i -й вершине.

Для неориентированного мультиграфа элемент r_ij равен единице, если вершина x_i инцидентна ребру u_j, и нулю, если вершина x_i не инцидентна ребру u_j.

Определение 2.4. Матрицей Кирхгофа графа G = (S, U), где 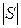= n, называется матрица B(G) = порядка n, где

 

 

Очевидно, что сумма элементов в каждой строке и каждом столбце матрицы B(G) равна нулю. Кроме того, из этого следует, что алгебраические дополнения всех элементов матрицы Кирхгофа равны между собой.

Пример 2.2. Для графа G, изображëнного на рис. 7, составить матрицы смежности вершин, смежности дуг и инциденций.

Решение. Матрица смежности вершин P (G):

 

 

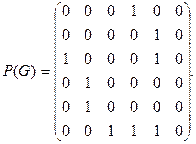
Матрица смежности дуг Q (G)и матрица инциденций R (G):



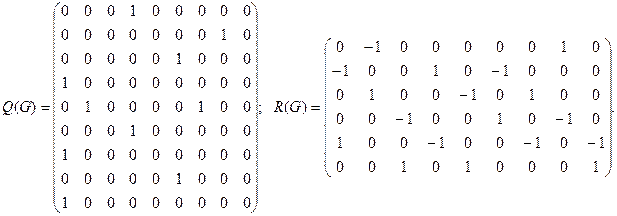
Изоморфные графы

Определение 3.1. Графы G₁ = (S₁, U₁) и G₂ = (S₂, U₂) называются изоморфными (G₁ @ G₂), если между множествами их вершин S₁ и S₂ можно установить такое взаимно однозначное соответствие, при котором две произвольные вершины смежны в одном из графов тогда и только тогда, когда соответствующие им вершины смежны в другом графе. В случае орграфов ориентация дуг также должна быть одинаковой.

Очевидно, что отношение «быть изоморфными» на множестве всех графов является отношением эквивалентности. Следовательно, множество всех графов разбивается на классы попарно изоморфных графов.

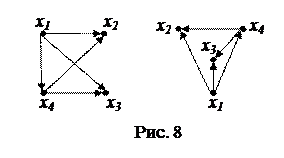Замечание 3.1. Диаграмма задает граф с точностью до изоморфизма. Это означает, что все различные диаграммы, содержащие одну и ту же информацию о вершинах и ребрах (дугах) графа и их взаимном расположении, являются изображениями одного и того же графа. Например, на рис. 8 представлено изображение одного и того же графа. 

Для того чтобы различать изоморфные графы, рассмотрим понятие помеченного графа.

Определение 3.2. Граф G порядка n называется помеченным, если его вершины занумерованы натуральными числами от 1 до n.

На рис. 9 изображены три разных помеченных графа порядка 3.

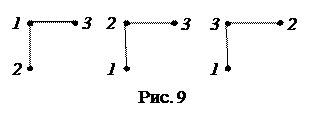Таким образом, под непомеченым (или абстрактным)графом следует понимать класс изоморфных графов.

Замечание 3.2. Структура графа однозначно определяется его матрицей смежности вершин. 

Теорема 3.1. Графы изоморфны тогда и только тогда, когда их матрицы смежности вершин получаются друг из друга в результате последовательности одновременных перестановок строк и столбцов (одновременно с перестановкой i -й и j -й строк переставляются i -й и j -й столбцы). 

Из теоремы 3.1 следует, что ранги матриц смежности вершин изоморфных графов равны. Это позволяет ввести в рассмотрение следующее определение.

Определение 3.3. Рангом графа G (rank G) называется ранг его матрицы смежности вершин P(G).

Замечание 3.3. Структура мультиграфа однозначно определяется его матрицей инциденций. 

Теорема 3.2. Мультиграфы изоморфны тогда и только тогда, когда их матрицы инциденций получаются друг из друга в результате последовательности произвольных перестановок строк и столбцов. 

 

Взвешенные графы

В различных приложениях теории графов ребрам (дугам) графов, представляющих собой модели реальных процессов, ставятся в соответствие какие-либо числовые характеристики. Например, если орграф изображает железнодорожную сеть, соединяющую несколько городов, то числовой характеристикой дуги может быть расстояние между городами. В таких случаях говорят, что дугам графа приписаны определëнные веса.

Определение 4.1. Орграф G = (S, U) называется взвешенным орграфом или ориентированной сетью, если каждой дуге (x_i, x_j)Î U поставлено в соответствие некоторое число w (x_i, x_j). При этом вершины орграфа называются узлами сети, а число w (x_i, x_j) – весом дуги (x_i, x_j).

Понятие взвешенного неорграфа или неориентированной сети определяется аналогично.

Простой взвешенный граф может быть также задан своей матрицей весов W = (w_ij), где w_ij – вес дуги (x_i, x_j). Веса несуществующих дуг полагают равными нулю или бесконечности в зависимости от приложений.

 

Подграф

Определение 5.1. Граф G ¢= (S ¢, U ¢) называется подграфом графа G = (S, U), если S ¢Í S, а U ¢ – множество всех ребер G, оба конца которых принадлежат S ¢.

Определение 5.2. Подграф называется собственным, если он отличен от самого графа.

Определение 5.3. Граф G ¢= (S ¢, U ¢) называется частью графа G = (S, U), если S ¢Í S, а U ¢ – подмножество множества всех ребер G, оба конца которых принадлежат S ¢.

Любой подграф графа является его частью, но не любая часть графа есть его подграф.

Так как подграф G ¢ полностью определяется множеством S ¢ своих вершин, то его можно обозначать кратко через G ¢(S ¢). Поэтому подграф G ¢= (S ¢, U ¢) называют также графом, порождëнным множеством S ¢ (или вершинно-порождëнным графом).

Пример 5.1. На рис. 10 изображены граф G, его подграф, порождëнный множеством вершин x₁, x₂, x₄, и его часть, содержащая все вершины G, но не все его рëбра. 

 

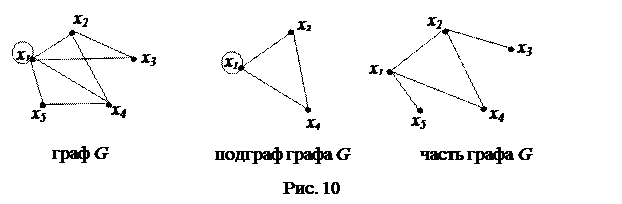
Все приведëнные определения распространяются на орграфы.

Определим на множестве подграфов графа G отношение включения. Пусть G ¢(S ¢) и G ²(S ²) – подграфы графа G. Говорят, что G ¢(S ¢) содержится в G ²(S ²) (пишут G ¢Í G ²), если S ¢Í S ². Легко видеть, что отношение включения подграфов графа G является отношением частичного порядка. При этом граф G является единственным максимальным элементом. Справедливо следующее утверждение.

Утверждение 5.1. Пусть G = (S, U) – произвольный псевдограф (ориентированный или неориентированный), S ¢Í S, S ¢ ¹ Æ и G ¢(S ¢) – подграф графа G. Тогда матрица смежности вершин P (G ¢) подграфа G ¢ является подматрицей матрицы смежности вершин P (G) графа G, находящейся на пересечении строк и столбцов, соответствующих вершинам из S ¢. 

Определение 5.4. Кликой называется полный подграф G ¢(S ¢) графа G.

Определение 5.5. Звездой вершины x называется часть графа G, содержащая вершину x, все инцидентные ей ребра и все смежные с x вершины.

Пример 5.2. На рис. 11изображены граф G, клика графа G и звезда вершины x₅ графа G. 

Замечание 5.1. Звезда вершины x является подграфом тогда и только тогда, когда любые две смежные с х вершины не соединены ребром. 

Понятие звезды вершины для орграфа, как и степень вершины, расщепляется на две части.

Определение 5.6. Полузвездой исхода (захода) вершины x орграфа называется подграф, порождëнный вершиной x и всеми вершинами, в которые из x

(из которых в x) ведут рëбра.

Операции над графами

Рассмотрим некоторые основные операции, позволяющие из уже имеющихся графов получать новые графы.

1. Объединение (сумма) графов. Объединением G₁ È G₂ графов G₁ = (S₁, U₁) и G₂ = (S₂, U₂) называется граф (S₁ È S₂, U₁ È U₂).

2. Пересечение (произведение) графов. Пересечением G₁ Ç G₂ графов

G₁ = (S₁, U₁) и G₂ = (S₂, U₂), где S₁ Ç S₂ ¹ Æ, называется граф (S₁ Ç S₂, U₁ Ç U₂).

3. Дополнение простого графа. Дополнением простого графа G = (S, U) называется простой граф 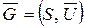, имеющий те же вершины, что и граф G, причëмлюбые две различные вершины смежны в 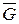тогда и только тогда, когда они не смежны в G.

4. Прямое произведение графов. Граф G = (S, U) называется произведением G₁ ´ G₂ графов G₁ = (S₁, U₁) и G₂ = (S₂, U₂), если S = S₁ ´ S₂, а множество рëбер U образуется следующим образом: вершины (x₁, x₂) и (y₁, y₂) смежны в графе G тогда и только тогда, когда либо вершины x₁ и y₁ совпадают, а вершины x₂ и y₂ смежны в G₂, либо вершины x₂ и y₂ совпадают, а вершины x₁ и y₁ смежны в G₁.

5. Удаление вершины. Операция, заключающаяся в удалении из графа

G = (S, U) вершины x и всех инцидентных ей рëбер (дуг), называется операцией удаления вершины x из графа G. В результате получается подграф G (S \{ x }).

6. Удаление ребра (дуги). Операция, заключающаяся в удалении ребра (дуги) u из множества рëбер (дуг) U графа G = (S, U), называется операцией удаления ребра (дуги) u из графа G. Концы ребра (дуги) u не удаляются.

7. Добавление вершины. Операция, которая из графа G = (S, U) порождает граф G ¢ = (S È{ x }, U), называется операцией добавления вершины x к графу G.

8. Добавление ребра (дуги). Операция, которая из графа G = (S, U) порождает граф G ¢= (S È{ x, y }, U È{(x, y)}, называется операция добавления ребра (дуги)

(x, y)к графу G.

9. Отождествление вершин. Пусть x и y – две произвольные вершины графа

G = (S, U). Операцией отождествления вершин x и y называется операция, заключающаяся в удалении из графа G вершин x и y и присоединении к полученному графу новой вершины z, соединив еë ребром (дугой) с каждой из вершин, входящих в объединение M множеств вершин, смежных с вершинами x и y в графе G. Если G – орграф, то для любой вершины a Î M присоединяется дуга

(a, z), если (a, x)Î U или (a, y)Î U, и дуга (z, a), если (x, a)Î U или (y, a)Î U.

10. Стягивание ребра (дуги). Операцией стягивания ребра (дуги) называется отождествление двух смежных вершин. Граф G называется стягиваемым к графу G₁, если G₁ получается из G в результате некоторой последовательности стягиваний рëбер (дуг).

11. Операция подразбиения ребра (дуги). Операцией подразбиения ребра (дуги) (x, y) графа G = (S, U) называется операция, заключающаяся в удалении из U ребра (дуги) (x, y), добавлении к S новой вершины z и добавлении к

U \ {(x, y)} двух рëбер (x, z) и (z, y).

Маршруты, цепи, циклы

Определение 7.1. Пусть G = (S, U) – граф (орграф). Чередующаяся последовательность его вершин и рëбер (дуг)

x₁, u₁, x₂, u₂, …, x_k, u_k, x_k+1 (7.1)

(где k ³ 1, x_i Î S, i = 1, …, k +1, u_j Î U, j = 1, …, k) такая, что для каждого

j = 1, …, k ребро (дуга) u_j имеет вид (x_j, x_j+1), называется маршрутом, соединяющим вершины x₁ и x_k+1 (путëм из вершины x₁ в вершину x_k+1). При этом вершина x₁ называется начальной, а вершина x_k+1 – конечной.

Очевидно, что маршрут можно задать последовательностью его вершин

x₁, x₂, …, x_k+1 или последовательностью ребер u₁, u₂, …, u_k.

Определение 7.2. Длиной маршрута (пути) называется число рëбер (дуг) в маршруте (пути).

Определение 7.3. Маршрут (путь) называется замкнутым, если его начальная и конечная вершины совпадают (т.е. x₁ = x_k+1).

Определение 7.4. Цепью называется незамкнутый маршрут (путь), в котором все рëбра (дуги) попарно различны.

Определение 7.5. Простой цепью называется цепь, в которой все вершины попарно различны.

Определение 7.6. Циклом (контуром) называется замкнутый маршрут (путь), в котором все рëбра (дуги) попарно различны.

Определение 7.7. Простым циклом (контуром) называется цикл(контур), в котором все вершины попарно различны.

Пример 7.1. Рассмотрим граф на рис. 12. Привести пример (незамкнутого) маршрута, замкнутого маршрута, цепи (не являющейся простой), простой цепи, цикла (не являющегося простым), простого цикла.

Решение. Пример (незамкнутого) маршрута: x₁ - x₇ - x₃ - x₄ - x₆ - x₉ - x₈.

Пример замкнутого маршрута:

x₁ - x₂ - x₆ - x₅ - x₄ - x ₆ - x₇ - x₁.

Пример цепи (не являющейся простой):

x₉ - x₆ - x₂ - x₁ - x₇ - x₆ - x₄.

Пример простой цепи:

x₈ - x₇ - x₃ - x₄ - x₅ - x₆ - x₂.

Пример цикла (не являющегося простым):

x₁ - x₂ - x₆ - x₉ - x₄ - x₆ - x₇ - x₁.

Пример простого цикла:

x₇ - x₃ - x₄ - x₆ - x₉ - x₈ - x₇. 

Связность. Компоненты связности

Определение 8.1. Граф (орграф) называется связным (сильно связным), если для любых двух его различных вершин существует маршрут (путь), соединяющий вершины x и y (из x в y).

Говорят, что вершина y орграфа (графа) G достижима из вершины x, если либо y = x, либо существует путь из x в вершину y (маршрут, соединяющий вершины x и у).

Таким образом, орграф G является сильно связным, если любые две его вершины взаимно достижимы.

Определение 8.2. Неориентированным псевдографом, ассоциированным с ориентированным псевдографом G = (S, U), называется неориентированный

псевдограф F (G), полученный из G заменой всех ориентированных рëбер на неориентированные.

Определение 8.3. Орграф G называется слабо связным,если ассоциированный с ним неориентированный псевдограф F (G) является связным.

Определение 8.4. Граф (орграф) называется несвязным, если он не является связным (слабо связным).

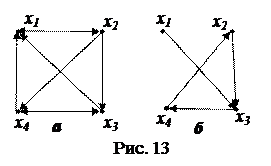Пример 8.1. На рис. 13 а изображëн сильно связный орграф, а на рис. 13 б – слабо связный орграф, т.к., например, вершина x₂ не достижима из вершины x₁. 

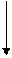
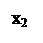
Замечание 8.1. Любой связный неориентированный граф является сильно связным. 

Определение 8.5. Всякий максимальный по включению (сильно) связный подграф данного графа называется его (сильной) связной компонентой, или (сильной) компонентой связности.

Утверждение 8.1. Пусть G = (S, U) – псевдограф с k компонентами связности:

G₁ = (S₁, U₁), …, G_k = (S_k, U_k). Тогда

1) S = S₁ È …È S_k, U = U₁ È…È U_k, т.е. G = G₁ È…È G_k;

2) S_i Ç S_j = Æ, U_i Ç U_j = Æ при i ¹ j;

3) 

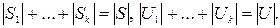
Утверждение 8.2. Пусть G = (S, U) – ориентированный псевдограф с k компонентами сильной связности: G₁ = (S₁, U₁), …, G_k = (S_k, U_k). Тогда

1) S = S₁ È …È S_k, U₁ È…È U_k Í U;

2) S_i Ç S_j = Æ, U_i Ç U_j = Æ при i ¹ j;

3) 

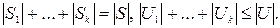
Рассмотрим задачи нахождения сильных компонент орграфа и всех маршрутов, состоящих из рëбер (дуг) графа.

Пусть P (G) – матрица смежности вершин орграфа G = (S, U) порядка n. Обозначим через матрицу B = (b_ij) квадратную матрицу порядка n, удовлетворяющую условию: B = E + P + P² + …+ Pⁿ.

Определение 8.6. Квадратная матрица C = (c_ij) порядка n, где

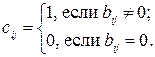
называется матрицей достижимости орграфа G.

Заметим, что элемент c_ij равен единице тогда и только тогда, когда в орграфе G существует путь из вершины x_i в вершину x_j.

Определение 8.7. Квадратная матрица L = (l_ij) порядка n, где

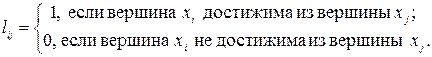
называется матрицей контрдостижимости орграфа G.

Известно, что L = C^T. Матрицы С и L используются для нахождения сильных компонент связности графа.

Определение 8.8. Квадратная матрица F = (f_ij) порядка n, удовлетворяющая условию F = C * L, где операция * означает поэлементное произведение матриц C и L (т.е. f_ij = c_ij · l_ij для любых i и j), называется матрицей сильных компонент связности орграфа G.

Элемент f_ij матрицы F равен единице тогда и только тогда, когда вершины x_i и x_j взаимно достижимы. Таким образом, множество вершин некоторой сильной компоненты связности G_p = (S_p, U_p) орграфа G = (S, U), кроме вершины x_i, содержит также все вершины x_j Î S, для которых f_ij = 1.

Для определения количества маршрутов с заданным количеством рëбер (дуг) графа используется следующая теорема.

Теорема 8.1. Пусть P (G) – матрица смежности вершин графа G = (S, U) порядка n и – k -я степень матрицы P. Тогда элемент 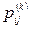матрицы P^k равен числу маршрутов, состоящих из k ребер (дуг) графа G из вершины x_i в вершину x_j. 

Пример 8.1. Найти сильные компоненты связности орграфа G, изображенного на рис. 14, и все маршруты длины три дуги, исходящие из вершины x ₁.

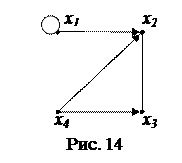Решение. Найдем матрицу смежности вершин

орграфа G:

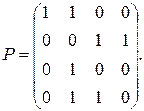Так как порядок орграфа G равен

 

четырем, то для нахождения матрицы B вычислим P^k, где k = 1, 2, 3, 4:

 

 

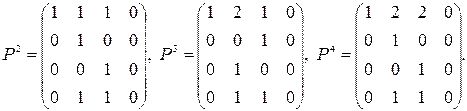
Следовательно, B = E + P + P² + P³ + P⁴ = 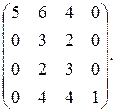Найдем матрицы

 

достижимости и контрдостижимости орграфа G:

Отсюда получаем матрицу

сильных компонент связности орграфа G: F = C * L =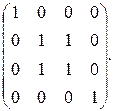

 

Таким образом, данный орграф G содержит три сильные компоненты связности G₁ = (S₁, U₁), G₂ = (S₂, U₂) и G₃ = (S₃, U₃), где S₁ = { x₁ }, S₂ = { x₂, x₃ },

S₃ = { x₄ }, диаграммы которых изображенные на рис. 15.