При проведении медико-биологических исследований на двух сравниваемых совокупностях возникает необходимость определить не только их различие, но и его достоверность.
Для оценки достоверности различия сравниваемых средних величин используется формула:
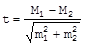,а для относительных величин: 
,
где Μ1, Μ2, P1 и P2 - статистические величины, полученные при проведении выборочных исследований: m1 и m2 - их ошибки репрезентативности; t - коэффициент достоверности. Различие достоверно при t>2. что соответствует вероятности безошибочного прогноза равной или более 95%. При величине коэффициента достоверности t<2 степень вероятности безошибочного прогноза менее 95%. При такой степени вероятности мы не можем утверждать, что полученная разность показателей достоверна с достаточной степенью вероятности. В этом случае необходимо получить дополнительные данные, увеличив число наблюдений. Если после увеличения численности выборки, и. соответственно, уменьшения ошибки репрезентативности, различие продолжает оставаться недостоверным, можно считать доказанным, что между сравниваемыми совокупностями не обнаружено различий по изучаемому признаку.
В качестве примера сопоставим уровни общей летальности в двух больницах:
| Больница N1 | Больница N2 | |
| Количество лечившихся больных | 4350 чел. | 6780 чел. |
| Из них умерло | 261 чел. | 135 чел. |
| Летальность | 6.0% (Р1) | 2.0% (P2) |
а) рассчитываем средние ошибки показателей летальности (Р1 и Р2).
б) вычисляем критерий достоверности t:
Рассчитанный критерий достоверности равен 10, он больше 2, что указывает на существенную разницу уровней летальности в сравниваемых больницах.
Корреляционный анализ
Многие явления в медицине, так же, как в природе и обществе, взаимосвязаны между собой. При проведении статистического исследования часто возникает необходимость проанализировать выявленные связи между различными явлениями и дать обобщающую характеристику. Различают 2 Формы проявления связей между явлениями: функциональную и корреляционную.
Функциональная связь означает строгую зависимость одного признака от другого, когда определенному значению одной величины соответствует стр о г о определенное значение другой. Например, радиусу круга соответствует определенная площадь круга; скорость свободно падающего тела определяется величиной ускорения, силы тяжести и времени падения. Функциональная связь характерна для физико-химических процессов.
Корреляционная связь - это такая связь, когда изменение какого-либо одного признака ведет к изменению другого, но на неопределенное значение.
Врачи и биологи хорошо знакомы с этим видом связи. Корреляционная связь проявляется между ростом детей и их родителей, массой тела и ростом, числом эритроцитов и содержанием гемоглобина, дозой зараженного агента и летальностью животных и т.д.
Корреляционная зависимость отличается по форме, направлению и силе связи.
По форме корреляционная связь может быть прямолинейной и криволинейной. Прямолинейная связь - равномерные изменения одного признака соответствуют равномерным изменениям второго признака при незначительных отклонениях. Криволинейная связь - равномерные изменения одного признака, соответствуют неравномерным изменениям второго признака, причем неравномерность имеет определенную закономерность. Общая тенденция в определенном моменте изменяет свое направление, дает изгиб.
Направление связи может быть прямое (положительное) или обратное (отрицательное).
Прям а я связь - если с увеличением одного признака второй также увеличивается или с уменьшением одного признака другой тоже уменьшается. Например, с увеличением роста увеличивается масса тела, с уменьшением заболеваемости уменьшается смертность. Обратн а я связь - когда с увеличение одного признака, другой, корреляционно связанный с ним признак, уменьшается. Например, с увеличением охвата прививками уменьшается заболеваемость инфекционными болезнями, с увеличением санитарной грамотности и образованием матери уменьшается младенческая смертность.
Под силой связи следует понимать степень корреляции.
Таблица 7
Критерии оценки коэффициента корреляции
| СТЕПЕНЬ СВЯЗИ | Величина коэффициента корреляции | |
| при прямой | при обратной | |
| Малая (слабая) | от 0 до +0.3 | от 0 до -0.3 |
| Средняя (умеренная) | от 0.3 до +0.69 | от -0.3 до -0.69 |
| Большая (сильная) | от 0.7 до +0.99 | от -0.7 до -0.99 |
| Функциональная | +1 | -1 |
Измерение силы связи осуществляется путем вычисления коэффициента корреляции. Рассмотрим два способа расчета коэффициента корреляции.
I. Парный коэффициент корреляции рядов (rху) вычисляется по формуле:
Рассмотрим на примере методику расчета коэффициента корреляции этим методом (Таблица 8).
Таблица 8
| Показатели | Отклонения | Квадрат отклонения | |||||
| железа в г%, VX | гемоглобина в %, Vy | dx | dy | dx*dy | dx2 | dy2 | |
| - 4 | -4 | ||||||
| - 4 | -3 | ||||||
| -3 | -1 | ||||||
| -2 | -1 | ||||||
| -1 | -1 | ||||||
При сопоставлении показателей содержания железа и гемоглобина в крови отмечается увеличение уровня гемоглобина с ростом количества железа. Следует определить степень связи между этими показателями и достоверность полученного результата.
Вычисления проводятся по следующему алгоритму: 1) Вычисляем средние арифметические рядов X и Y:
2) Определяем отклонения вариант каждого ряда от своей средней (dx и dу): смотри графы 3 и 4 в Таблице 3.
3) Находим произведение dx*dy: смотри графу 5 в Таблице 8. Полученные значения суммируются с учетом знаков.
4) Возводим в квадрат dx и dy и суммируем полученные значения: смотри графы 6 и 7 в Таблице 8.
5) Вычисляем коэффициент корреляции:
Вывод: Отмечается очень сильная корреляционная связь между содержанием в крови железа и гемоглобина.
Для оценки достоверности коэффициента корреляции вычисляется его средняя ошибка:
- при числе наблюдений более 100;
- при числе наблюдений от 30 до 100;
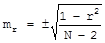- при числе наблюдений менее 30.
В рассматриваемом нами примере следует использовать последнюю формулу, поскольку число наблюдений равно 9:
Для оценки величины полученной ошибки следует использовать критерий достоверности (t).
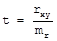
При числе наблюдений более 30 коэффициент корреляции достоверен, если критерий t больше или равен 3. При числе наблюдений менее 30 критерий t оценивается по специальной.
В рассматриваемом нами примере 
Это больше табличного значения, что подтверждает достоверность выявленной сильной связи и взаимозависимости анализируемых явлений.
II. Ранговый коэффициент корреляции (ρ) относится к непараметрическим критериям и предложен Спирменом. Он используется при необходимости получения быстрого результата и основан на определении ранга (места) каждого из значений ряда.
Для вычисления рангового коэффициента корреляции используется следующая формула:
Рассмотрим методику вычисления рангового коэффициента корреляции на следующем примере (Таблица 9).
Таблица 9.
| Годы | Число травм на 100 рабочих | Число гнойничковых заболеваний на 100 рабочих | Ранги | dxy | d2xy | |
| х | у | |||||
| 5.0 | 4.0 | -1 | ||||
| 6.1 | 3.5 | +1 | ||||
| 9.0 | 4.8 | +1 | ||||
| 8.6 | 5.5 | -1 | ||||
| 7.4 | 4.2 |
При сопоставлении частоты травматизма и распространенности гнойничковых заболеваний среди рабочих промышленного предприятия отмечается рост гнойничковых заболеваний с увеличением травматизма. Следует определить степень связи между этими показателями и достоверность полученного результата.
Вычисления проводятся по следующему алгоритму:
1) Определяем ранги по значению каждой величины ряда. Важно соответствие. Если первый ряд ранжируется от меньшего значения к большему, то второй ряд следует ранжировать в том же порядке.
2) Отмечаем отклонение значимости рангов первого ряда от второго (dxy): смотри графу 6 в таблице 9. Они в сумме с учетом знаков равны нулю.
3) Возводим в квадрат полученные отклонения и суммируем их. В нашем примере d2xy = 4: смотри графу 7 в таблице 9.
4) Рассчитываем ранговый коэффициент корреляции:
Вывод: Корреляция прямая, высокая. Между травматизмом и частотой гнойничковых заболеваний на предприятии существует тесная связь.
Оценка достоверности полученного рангового коэффициента корреляции выполняется по методике, которая была разобрана для коэффициента корреляции рядов.
Регрессионный анализ
Прямолинейная корреляция отличается тем, что при этой Форме связи каждому значению одного признака соответствует определенное в среднем значение другого признака.
Та величина, на которую в среднем изменяется второй признак при изменении первого на единицу, называется коэффициентом регрессии.
Для расчета коэффициента регрессии используется следующая формула:
Рассмотрим методику расчета коэффициента регрессии на примере.
При анализе физического развития 7-летних мальчиков были получены следующие средние значения роста (X) и массы тела (У):
| X = 118.4 см | х = +/-6.0 см |
| У = 24.0 кг | у = +/-2.6 кг |
Коэффициент корреляции между весом и ростом составил +0.7. Расчет коэффициента регрессии выполняется по формуле:
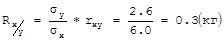
Следовательно, с изменением роста 7-летних мальчиков на 1 см. масса тела в среднем изменяется на 0.3 кг.
С помощью коэффициента регрессии без специальных измерений можно определить величину одного из признаков (например, массы тела), зная значение другого (роста). С этой целью используется ур а внени е лине й ной регрессии:
у = My + Rxy(х - Мх),
где у - искомая величина массы тела;
My - среднее значение массы тела, характерное для данного
возраста;
Rxy - коэффициент регрессии массы тела по росту;
х - известная величина роста;
Мх - средне значение роста.
Определим, какова будет масса тела 7-летнего мальчика при росте 120 см.
у = Мy + Rxy(х - Мх) = 24 + 0.3(120 - 118) = 24.6 кг
Коэффициенты регрессии и уравнения регрессии широко применяются для составления шкал регрессии, которые используются при индивидуальной оценке физического развития.
ДИНАМИЧЕСКИЕ РЯДЫ
При изучении динамики какого-либо явления прибегают к построению динамического ряда.
Динамический ряд - это ряд однородных статистических величин, показывающих изменение какого-либо явления во времени и расположенных в хронологическом порядке через определенные промежутки времени.
Числа, составляющие динамический ряд, называются уровнями.
У ровень ряда - размер (величина) того или иного явления, достигнутый в определенный период или к определенному моменту времени.
Уровни ряда могут быть представлены абсолютными, относительными или средними величинами.
Динамические ряды делятся на простые (состоящие из абсолютных величин) и сложные (состоящие из относительных или средних величин).
Простые динамические ряды могут быть моментными и интервальными.
Моментный динамический ряд состоит из величин, характеризующих явление на какой-то определенный момент (дату). Примером могут служить статистические сведения, обычно регистрируемые на начало или конец месяца, квартала, года (численность населения на начало года, число врачей, средних медицинских работников на конец года, число лечебных учреждений, коек на конец года и т.д.).
Интерв а льный динамический ряд состоит из чисел, характеризующих явление за определенный промежуток времени (интервал) - за неделю, месяц, квартал, год и т. д. Примером такого ряда могут служить данные о числе родившихся, умерших за год, число инфекционных заболеваний за месяц и т. д. Особенностью интервального ряда является то, что его члены можно суммировать (при этом укрупняется интервал), или дробить. Например, имея данные о количестве заболевших дизентерией, зарегистрированных за каждые день, можно построить динамический ряд с интервалом в неделю, месяц, год.
Динамические ряды могут подвергаться преобразованиям, целью которых является выявление особенностей изменения изучаемого процесса, а также достижение наглядности.
Прежде всего ряд может быть охарактеризован самими величинами членов ряда, называемыми уровнями. Величина первого члена ряда носит название начального (исходного) уровня, величина последнего члена ряда - конечного уровня. Средняя величина из всех членов ряда называется средним уровнем.
Абсолютный прирост (убыль) - величина разности между последующим и предыдущим уровнями; прирост выражается числами с положительным знаком, убыль - с отрицательным знаком. Значение прироста или убыли отражают изменения уровней динамического ряда за определенный промежуток времени.
Темп рост а (снижения) - показывает отношение каждого последующего уровня к предыдущему уровню и обычно выражается в процентах.
Темп прирост а (убыли) - отношение абсолютного прироста или убыли каждого последующего члена ряда к уровню предыдущего, выраженное в процентах. Темп прироста может быть вычислен также по формуле: Темп роста - 100%
Абсолютное значение одного процента приро с та (убыли) - получается от деления абсолютной величины прироста или убыли на показатель темпа прироста или убыли за тот же период.
Для более наглядного выражения нарастания или убывания ряда можно преобразовать его путем вычисления показателей наглядности, показывающих отношение каждого члена ряда к одному из них, принятому за сто процентов.
Примеры расчета показателей динамического ряда представлены в таблице 10.
Таблица 10
Младенческая смертность в Индии в 1992-1995гг. (на 1000)
| Годы | Показатель заболеваем. | Абсолютный прирост | Темп роста | Темп прироста % | Показатель наглядности % |
| 95.0 | - | - | - | 100% | |
| 98.0 | + 3.0 | 103% | + 3.2% | 103% | |
| 96.0 | - 2.0 | 97% | - 2.0% | 101% | |
| 87.9 | - 8.1 | 91% | - 8.4% | 95.5% |
Абсолютный прирост (убыль):
1993: 98.0 - 95.0 = + 3.0
1994: 96.0 - 98.0 = - 2.0
1995: 87.9 - 96.0 = - 8.1
Темп роста (убыли):
; 
Темп прироста (убыли):
; 
; 
Показатель наглядности:
1992: = 100%; ;
; 
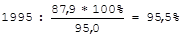
Иногда динамика изучаемого явления представлена не в виде непрерывно меняющегося уровня, а отдельными скачкообразными изменениями. В этом случае для выявления основной тенденции в развитии изучаемого явления прибегают к выравниванию динамического ряда. При этом могут быть использованы следующие приемы: укрупнение интервала, вычисление групповой средней, вычисление скользящей средней, выравнивание методом наименьших квадратов.
Укрупнение интервала производят путем суммирования данных за ряд смежных периодов. В результате получаются итоги за более продолжительные промежутки времени. Этим сглаживаются случайные колебания и более четко определяется характер динамики явления.
Вычисление групповой средней заключается в определении средней величины каждого укрупненного периода. Для этого необходимо суммировать смежные уровни соседних периодов, а затем сумму разделить на число слагаемых. Этим достигается большая ясность изменений во времени.
Вычисление скользящей средней в некоторой степени устраняет влияние случайных колебаний на уровни динамического ряда и более заметно отражает тенденцию явления. При ее вычислении каждый уровень ряда заменяется на среднюю величину из данного уровня и двух соседних с ним. Чаще всего суммируются последовательно три члена ряда, но можно брать и больше
Пример выравнивания динамического ряда данных о заболеваемости дизентерией по месяцам года представлен в таблице 11.
Таблица 11.
Число заболеваний дизентерией по месяцам года
| Месяцы | Число больных | Число больных за квартал | Групповая средняя | Скользящая средняя |
| - | ||||
| 8:3=2.6 | 2.7 | |||
| 3.7 | ||||
| 4.7 | ||||
| 20:3=6.6 | 6. 7 | |||
| 9. 0 | ||||
| 13.0 | ||||
| 45:3=15 | 15.0 | |||
| 15.7 | ||||
| 12.7 | ||||
| 20:3=9.6 | 9.7 | |||
| - |
Увеличивая в данном динамическом ряду интервал до 3 месяцев получаем число заболевших за квартал (графа 3, табл.11). Полученные данные указывают на постепенное возрастание числа заболевших дизентерией и его максимум в 3 квартале, после чего заболеваемость снижается.
Разделив каждую полученную сумму на 3 (число месяцев в квартале), получаем средние величины по группам, отражающие ту же закономерность (графа 4. табл.11).
Скользящая средняя обычно вычисляется как средня арифметическая из 3 смежных уровней (данного, предыдущего и последующего). Для первого и последнего уровней скользящая средняя не рассчитывается (графа 5, табл.11).
Для 2-го уровня: 
= 2, 7; для 3-го уровня: 
= 3.7 и т. д.
Метод наименьших квадратов - один из наиболее точных способов выравнивания динамического ряда. Этот метод преследует цель устранить влияние временно действующих причин, случайных факторов и выявить основную тенденцию в динамике явления, вызванную воздействием только длительно действующих факторов. Выравнивание производится по линии, наиболее соответствующей характеру динамики изучаемого явления, при наличии основной тенденции к росту или снижению частоты явления. Такой линией является обычно прямая, которая наиболее точно характеризует основное направление изменений. Этот метод позволяет дать количественную оценку выявленной тенденции и на этой основе рассчитать прогнозируемые уровни на следующий год.
ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ
Результаты статистического исследования могут быть представлены в виде графических изображений, что позволяет более наглядно продемонстрировать полученные результаты и облегчает проведение анализа.
Существует несколько видов графических изображений, наиболее часто используют диаграммы (линейные, радиальные, столбиковые, ленточные, гистограммы, секторные и др.), картограммы, картодиаграммы (рис. 1-8)
При построении графических изображений необходимо соблюдать следующие правила:
- данные на графике должны размещаться слева направо и снизу вверх;
- обязательное условие при построении графика - соблюдение масштабности;
- нулевые точки шкал при наличии возможности должны быть изображены на диаграмме)
- цифры, показывающие деление шкал, помещаются слева или внизу соответствующей шкалы;
- линии, представляющие диаграмму изображаемого явления, следует делать иного вида, нежели вспомогательные линии;
- на кривой, отражающей динамику явления, необходимо отметить все точки, соответствующие отдельным наблюдениям;
- в диаграммах, показывающих структуру, должна быть оттенена как линия нулевая, так и 100-процентная;
- изображенные графические величины должны иметь цифровые обозначения на самом графике или в прилагаемой к нему таблице;
- символы, используемые при построении диаграммы (цвет, штриховка, фигуры, знаки), должны быть пояснены;
- каждый график должен иметь четкое, краткое название, отражающее его содержание;
- название диаграммы должно размешаться под рисунком.
Линейные диаграммы позволяют изображать динамику явления (изменение показателей во времени). Линейная диаграмма строится в системе прямоугольных координат, при ее построении следует учитывать соотношение между основанием и высотой - абсциссой х и ординатой у, основанное на принципе "золотого сечения": это соотношение должно быть 1,6:1. На горизонтальной оси (оси абсцисс) откладываются отрезки, обозначающие периоды времени. На вертикальной оси (оси ординат) откладываются размеры изучаемого явления. Обязательное условие при построении графика - масштабность. На одной диаграмме можно изобразить несколько линий, отличающихся друг от друга цветом, толщиной или формой пунктира (Рис.1).
Радиальные диагр а ммы (диаграммы полярных координат, линейно-круговые диаграммы, векторные диаграммы) применяются для изображения сезонных (подекадных, помесячных, поквартальных) и других колебаний, имеющих замкнутый, циклический характер (за сутки, неделю и т.д.). Для их построения круг делится на столько секторов, на сколько частей разделен период времени, взятый для изучения явления (например, на 12 - при изучении помесячных колебаний в течение года; на 7 - при изучении явления за неделю). На каждом из радиусов с соблюдением масштабности отмечаются показатели, полученные точки соединяют прямыми линиями. Начало маркировки радиусов начинается с радиуса, соответствующего нулю градусов, и продолжается по часовой стрелке (Рис.2).
Рис. 2 Сезонное распределение заболеваемости дизентерией в Ираке в 1997 году (1-12 - месяцы года)
Столбиковые ди а граммы строятся по такому же принципу, как и линейные, в системе координат, с соблюдением масштабности, но в которых вертикально или горизонтально проводимым линиям соответствуют прямоугольники. Эти диаграммы используются для изображения сравнительной величины явления в какой-либо определенный промежуток времени, например, сравнительной численности населения по странам мира; обеспеченности населения врачами в разные годы и т.д. (Рис.3).
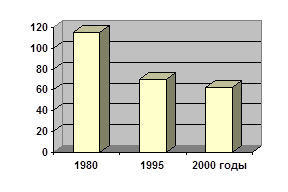
Рис. 3 Средние значения уровней младенческой смертности в странах Восточного Средиземноморья
Гистограммы - в виде прямоугольников, треугольников, фигур позволяют изобразить однородные статистические показатели, не связанные друг с другом. Эти диаграммы используются для графического изображения статистических величин, характеризующих статику явления в разных совокупностях. Они также строятся в системе прямоугольных координат с соблюдением масштабности. Например, гистограммы применяются для графического изображения уровней смертности в разных возрастных группах населения; для демонстрации показателей больничной летальности в различных стационарах города; для изображения распространенности туберкулеза в различных социально-бытовых группах населения и т.д. (Рис.4).
Рис.4 Численность медперсонала (на 100000 населения) по регионам мира: 1-Африка; 2-Восточное Средиземноморье: 3 — Юго—Восточная Азия
С екторные диаграммы используются для демонстрации структуры изучаемого явления, изображения части явления в целом. Они представляют собой круг, принимаемый за целое (100%), в котором отдельные секторы соответствуют частям изображаемого явления. Этот вид диаграмм применяется для графического изображения экстенсивных показателей. В секторных диаграммах секторы, изображающие отдельные части изучаемого явления, располагаются в порядке возрастания или убывания по движению часовой стрелки и имеют разный цвет или штриховку (Рис.5).
Условные обозначения:
1 - инфекционные болезни
2 - болезни системы кровообращения
3 - злокачественные новообразования
4 - болезни органов дыхания
5 - перинатальные причины
6 — другие причины
Рис. 5 Структура причин смерти в развивающихся странах в 1996 году
|
Внутристолбиковые диагр а ммы также могут применяться для изображения структуры явления. При этом высота столбика принимается за 100%, весь столбик делится на составные части, которые соответствуют долям явления в процентах (Рис.6).
Условные обозначения:
1 - 0-14 лет
2 - 15-59 лет
3 - 60 лет и старше
Рис.6 Возрастная структура населения Ирана в 1996
Картограммы - это графические изображения, нанесенные на схемы географической карты, на которой различным цветом или штриховкой изображены степени распространенности явления по территории (Рис.7).
Рис. 7. Распределение зарегистрированных случаев лепры в мире в 1996 г.
Картодиаграммы - такие графические изображения, при построении которых на карту или схему карты изучаемой территории проставляются диаграммы (столбиковые, фигурные, линейные) (Рис.8).
Рис. 8. Стандартизованные показатели заболеваемости взрослых раком шито-видной железы.
- 1961-1965гг. 
- 1990-1994гг.
ЛИТЕРАТУРА
1. Каминский Л.С. Статистическая обработка лабораторных и клинических данных. Ленинград. Медгиз, 1964.
2. Марков A.M.. Поляков Л.Е. Санитарная статистика (пособие для врачей). Ленинград. "Медицина". 1974.
3. Методические указания для студентов и аспирантов по применению основных статистических методов обработки научных исследований. Под ред. В.А.Минаева. Ленинград. 1989.
4. Плохинский Н.А. Биометрия. Москва. МГУ. 1870.
5. Поляков И.В., Соколова И. С. Практическое пособие по медицинской статистике. Ленинград, Медицина. 1874.
6. Руководство к практическим занятиям по социальной гигиене и организации здравоохранения. Под ред. Ю.П.Лисицына и Н.Я.Копыта. Москва, "Медицина", 1984.
7. Случанко А.С. Теория и методика санитарно-статистического исследования. Москва. 1986.
8. Социальная гигиена и организация здравоохранения. Под ред. А.Ф.Серенко и В.В.Ермакова. Москва. "Медицина", 1984.
9. Урбах В.Ю. Биометрические методы. Москва, 1964. 10. Учебное пособие по медицинской статистике (для студентов санитарно-гигиенических факультетов). Под ред. Е.Л.Белицкой. Ленинград. "Медицина". 1972.
