Для выполнения работы используются пружинный маятник, закрепленный на штативе, набор грузиков, секундомер, мерная линейка.
а б в
Рисунок 1 Положения пружинного маятника: а – без грузика; б – с грузиком в отсутствии колебаний; в – при смещении x грузика от положения равновесия в процессе колебаний
Зависимость периода колебаний T от параметров пружинного маятника: 
.
Отсюда жесткость пружины выразится как:
. (4)
В реальных колебательных системах всегда часть энергии расходуется на работу по преодолению сил трения (например, силы сопротивления воздуха, сил внутреннего трения и т.д.). При этом амплитуда колебаний A уменьшается со временем до нуля. Такие колебания называются затухающими.
При рассмотрении колебания в среде (в том числе и в воздухе), обладающей вязкостью, необходимо учесть силу сопротивления среды, значение которой прямо пропорционально скорости:
, (5)
где r называется коэффициентом сопротивления среды;
– скорость колеблющегося тела.
В этом случае второй закон Ньютона принимает вид:
. (6)
Перепишем (6), обозначив r / m = 2 b и k / m = w 02:
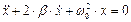, (7)
где b называется коэффициентом затухания.
Формула (7) является дифференциальным уравнением затухающих колебаний. При его решении можно рассмотреть 2 случая.
1) Случай малых затуханий b << w 0.
Потери энергии в системе малы. Решение имеет вид
x = A 0×exp (– b × t) × cos(w × t + j), (8)
где 
. Тогда период колебаний
(9)
увеличивается по сравнению с периодом незатухающих колебаний. Из выражения (8) следует, что амплитуда колебаний определяется следующим образом:
A (t) = A 0×exp (– b × t), (10)
т.е. со временем она убывает. Величина t = 1 / b называется временем релаксации – это время, в течение которого амплитуда колебаний уменьшается в e» 2,72 раз.
Изменение амплитуды колебаний во времени при не очень больших затуханиях показано на рисунке 2а, где пунктирные линии изображают функцию (10).
а б
Рисунок 2 Зависимость смещения от времени: а – случай
малых затуханий b << w 0; б – апериодический режим b > w 0
Из закона убывания амплитуд (10) следует, что отношение любых двух амплитуд, отстоящих друг от друга на один период, есть величина постоянная: A (t)/ A (t + T) = const = d.
Величину d называют декрементом затухания. Часто пользуются также понятием логарифмический декремент затухания l = ln d, который, как можно показать подстановкой d в (10) равен b × T. Отсюда b = l / T.
2) Случай b > w 0.
Потери энергии в системе велики. В этом случае в уравнении (7) третий член перестает играть существенную роль, и решение описывает апериодический режим движения (рисунок 2б).
Сопротивление среды, при котором колебания прекращаются, называется критическим. Оно находится из условия 
, или b = w 0: 
.
