К оформлению результатов
3.1 Перед занятием необходимо законспектировать следующий теоретический материал:
- для неинженерных специальностей: /1/ С.30-34, 53-62;
- для инженерных специальностей: /2/ С.19-21, 27-34; /3/ С.74-75, 95-97, 98-105.
Занести в конспект методику выполнения работы, необходимые таблицы и формулы (разделы 2, 3).
3.2 Измерить массу пули`` m взвешиванием, погрешность D m = D mинс, где D mинс – инструментальная погрешность. Масса маятника `` M и её погрешность D M указаны на лабораторной установке.
Поскольку средние значения и погрешности величин масс `` m, D m, `` M, D M входят в расчетные формулы (6) и (7) в отношениях друг к другу, то все они, при занесении в таблицу 1, должны быть указаны в одинаковых единицах измерения – либо в кг, либо допускается в г.
3.3 Измерить длину подвеса l. Абсолютную погрешность D l взять равной погрешности попадания пули в центр маятника при выстреле из ружья: D l = 0,005 м.
Занести в таблицу 1 значение g ± D g. Здесь D g – абсолютная погрешность табличной величины g составляет половину от точности ее представления C: D g = C / 2.
Например, если в работе берется значение g = 9,8 м/с 2, то точность ее представления C = 0,1 м/с 2, тогда D g = 0,05 м/с 2. Или, если берется g = 9,81 м/с 2, то C = 0,01 м/с 2, тогда D g = 0,005 м/с 2.
3.4 Вначале эксперимента отметить по шкале 3 положение стрелки 4 при неподвижном состоянии тела 2.
3.5 Произвести выстрел из воздушного ружья строго в центр маятника 2, отметить отклонение b маятника по шкале 3. Занести значение b в таблицу 2.
Опыт повторить не менее 5 раз.
Таблица 1 Табличные и однократно измеренные величины
| Обозначения физических величин | |||
| `` M ± D M, г | `` m ± D m, г | g ± D g, м/с 2 | ` l ± D l, м |
| 9,81 ± 0,005 |
Таблица 2 Экспериментальные и расчетные величины
| Обозначения физических величин | |||||
| № п/п | bi | D bi | (D bi)2 | ` u | D u |
| средние значения |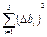 
| — | — |
3.6 Вычислить среднее значение отклонения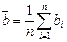 
, где n = 5 – количество опытов; абсолютные погрешности каждого измерения D bi = |` b – bi |; квадраты этих погрешностей (D bi)2. Найти сумму квадратов 
.
3.7 На основании известных уже величин `` M,`` m,` b, g,` l, вычислить среднее значение скорости пули ` u по формуле (6).
3.8 Рассчитать среднеквадратическое отклонение:
.
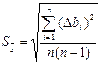По таблице коэффициентов Стьюдента из Приложения А найти tp,n для n =5 и выбранной доверительной вероятности, например p = 0,95.
Определить доверительный интервал для b: 
3.9 Сравнить найденный доверительный интервал D b с инструментальной погрешностью D bинс измерительной линейки и бо/льшую из них использовать для дальнейших расчетов, например, в формуле (7). (D bинс = c / 2, где c – цена деления линейки).
3.10 Вывести формулу относительной погрешности по следующей методике:
а) вначале логарифмируем исходную формулу (6)
ln u = ln M – ln m + ln b + ½×(ln g – ln l),
б) далее производим дифференцирование:
,
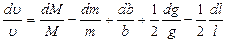в) в полученном выражении заменяем знаки дифференциалов d на знаки конечных приращений Δ: d ® Δ; заменяем (–) ® (+), и по правилам статистики берем сумму квадратов слагаемых. Окончательный вид формулы относительной погрешности:
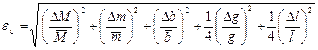. (7)
3.11 Определить абсолютную погрешность
D u = eu ×` u
и оставить в ней одну значащую цифру, используя правила округления (например, число 0,5861 следует записать как 0,6).
3.12 Провести округление величины u в соответствии с погрешностью D u (например, если D u представлено с точностью до десятых: D u = 0,6, то и `` u = 32,4835 надо округлить до десятых: ` u = 32,5).
Окончательный результат скорости пули представить в виде:
u = `(u ± D u) м/с,
например, u = (32,5 ± 0,6) м/с. (Примечание: здесь в качестве примера взяты произвольные числа, поэтому их не следует переписывать.)
Контрольные вопросы
4.1 Что является мерой инертности тела при поступательном движении? Единицы измерения?
4.2 Что называется импульсом? Это скалярная или векторная величина? В чём выражается суть закона изменения импульса? Что представляет собой импульс силы?
4.3 Привести примеры из практики на закон изменения импульса.
4.4 Что такое система тел? Какая система называется замкнутой (изолированной) и незамкнутой (неизолированной)?
4.5 Как формулируется и выражается математически закон сохранения импульса (в скалярной и векторной форме)? Привести примеры на закон сохранения импульса.
4.6 Какие виды энергии вы знаете (назвать и выразить формулой)? Сформулировать закон сохранения энергии.
4.7 Выполняется ли закон сохранения импульса в тех физических явлениях, где имеет место закон изменения энергии?
Лабораторная работа № 2
Изучение вращательного движения
и определение моментов инерции тел
Цель и задачи работы: Изучить основные характеристики вращательного движения. Экспериментально проверить второй закон Ньютона для вращательного движения – зависимость углового ускорения вращающегося тела от момента силы и его момента инерции. Определить момент инерции маятника Обербека при различных моментах силы. Исследовать зависимость момента инерции маятника в зависимости от положения грузиков.
Общие сведения
Рассмотрим твердое тело, вращающееся вокруг неподвижной оси. Его вращение характеризуется углом поворота j, угловой скоростью 
, угловым ускорением 
.
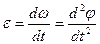Мерой инертности вращающегося тела является момент инерции J (его аналог при поступательном движении – масса m). Момент инерции материальной точки на расстоянии r от оси вращения, вычисляется по формуле J = m × r 2. Для расчета величины J твердого тела его надо рассмотреть как систему n материальных точек (разбить на n материальных точек) и вычислить момент инерции каждой из них Ji = mi × ri 2 и далее сложить: J = in=Sl mi × ri 2.
Воздействие на вращающееся тело некоторой силы ® F, не проходящей через ось вращения, вызывает изменение кинематических характеристик движения тела j, w, e. При этом, как и в случае поступательного движения, угловое ускорение e также пропорционально величине этого воздействия: e ~ F.
Однако в отличие от случая поступательного движения здесь внешнее воздействие зависит не только от величины F, но и расстояния l от оси вращения до прямой, вдоль которой действует сила (это расстояние называется плечо силы). При вращательном движении мерой воздействия является момент силы: M = F × l.
Также выполняется второй закон Ньютона для вращательного движения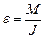 
(сравните 
– второй закон Ньютона для поступательного движения).
