В работе используются маятник Обербека, укрепленный на стене (рисунок 1), линейка, штангенциркуль, секундомер.
Особенности вращения твердого тела вокруг неподвижной оси удобно изучать на примере маятника Обербека – устройства, состоящего из крестовины, жестко закрепленной на двойном шкиве с разными радиусами (рисунок 1). На стержнях крестовины симметрично оси вращения закрепляются четыре одинаковых грузика 5. Расстояния от грузиков до оси вращения можно изменять.
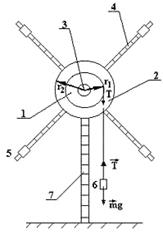
Рисунок 1 Схема маятника Обербека:
1, 2 ‑ двойной шкив с радиусами r 1 и r 2; 3 ‑ ось подшипника;
4 ‑ стержни с делениями; 5 ‑ грузики; 6 ‑ гиря; 7 ‑ мерная линейка
Поочередно на большой и малый шкивы можно наматывать нить, к концу которой привязана гиря 6 известной массы. Тем самым изменяется момент силы, вызывающий вращательное движение системы. Момент инерции вращающейся системы можно изменять, передвигая грузики 5 на стержнях. Главной измеряемой величиной в данной работе является промежуток времени t, за который гиря 6 проходит определенный путь h.
Выведем формулы для расчета момента силы и момента инерции. Выражения закона динамики образуют систему уравнений:
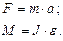(1)
Первое уравнение относится к поступательному движению гири 6. Результирующая сила F равна разности сил, действующих на гирю:
F = mg – T, (2)
где T – сила натяжения нити.
Из (2) и первого уравнения системы (1) T выразится как:
T = mg – F = m (g – а). (3)
Второе уравнение системы (1) относится к вращательному движению маятника, где момент силы М определяется силой натяжения T и плечом этой силы r, равным радиусу того шкива, на который намотана нить:
M = T × r = m (g – а) r. (4)
В выражении (4) не учитывается момент M тр сил трения, действующих в системе. Если им нельзя пренебречь, то результирующий момент примет вид:
M = m (g – а) r – M тр. (5)
Чтобы оценить влияние сил трения, можно проделать эксперимент на основе закона сохранения энергии. Задать гире некоторую высоту h 1 и предоставить систему самой себе. Маятник начнет вращаться, при этом гиря опустится, а затем поднимется до высоты h 2. Если h 1 > h 2, то произошла потеря потенциальной энергии, затраченная на работу против сил трения. Оценить эту потерю по относительной разнице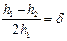 
. Если d £ 0,1 (10%), то моментом сил трения в работе можно пренебречь.
При отсутствии сил трения момент вращающей силы находят по формуле (4). Линейное a и угловое e ускорения – из кинематических уравнений:
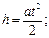
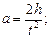
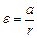. (6)
Первое задание выполняется при постоянном моменте инерции, но различных моментах силы М 1 и М 2 (используются различные шкивы – радиусов r 1 и r 2). Различны будут угловые ускорения e 1 и e 2. Моменты инерции для двух случаев
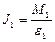и 
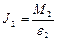, (7)
должны быть равны (в пределах допустимой погрешности), т.к. распределение массы относительно оси вращения не меняется, т.е. J 1 = J 2 = J, тогда должны быть равны и отношения:
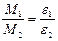. (8)
В этом и состоит проверка второго закона Ньютона для вращательного движения в задании 1
Для вывода расчетной формулы задания 2 объединим соотношения, описывающие динамику вращательного движения маятника Обербека и поступательного движения гири:
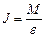; M=m (g – a) r; 
; 
.
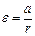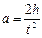Получим обобщенную формулу для расчета момента инерции:
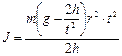, (9)
где t – время движения гири; h – расстояние, пройденное гирей массой m; r – радиус шкива, на который наматывается нить; g = 9,81 м/с 2 – ускорение свободного падения.
Поскольку а << g, то (9) можно представить в виде:
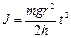. (10)
В этой формуле постоянный коэффициент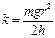 
можно вычислить один раз и применять для дальнейших расчетов:
J = k × t 2. (10а)
