Консервативных сил.
В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.
Для консервативных сил выполняются следующие тождества:
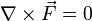— ротор консервативных сил равен 0;
— работа консервативных сил по произвольному замкнутому контуру равна 0;
— консервативная сила является градиентом некой скалярной функции U, называемой силовой. Эта функция равна потенциальной энергии взятой с обратным знаком.
В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости. Примерами неконсервативных сил являются сила трения и сила сопротивления среды.
В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной
Потенциальная энергия 
— скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.
Единицей измерения энергии в СИ является Джоуль.
Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.
Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.
Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.
Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
Ep = mgh,
где Ep — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
Закон сохранения энергии.
Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от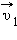 
до 
то силы совершили определенную работу A.
Работа всех приложенных сил равна работе равнодействующей силы (см. рис. 1.19.1).
|
Рисунок 1.19.1.
Работа равнодействующей силы.  . A = F 1 s cos α1 + F 2 s cos α2 = F 1s s + F 2s s = F рs s = F р s cos α.
|
Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы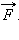 
В этом случае векторы силы 
перемещения 
скорости 
и ускорения 
направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
|
Отсюда следует, что
|
Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
|
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
|
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью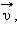 
равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
|
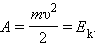
Если тело движется со скоростью 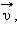то для его полной остановки необходимо совершить работу
|
Закон сохранения энергии: в системе тел, между которыми действуют только консервативные силы, полная механ энергия сохраняется, т.е. не изменяется во времени. Eк + Ep = E = const. Энергия превращается из одного вида в другой. Полная энергия тела- сумма потенциальной и кинетической энергии тела. EK2+EP2=EK1+EP2.
