Линейное перемещение, линейная скорость, линейное ускорение.
Перемеще́ние (в кинематике) — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Обладает свойством аддитивности. Длина отрезка — это модуль перемещения, измеряется в метрах (СИ).
Можно определить перемещение, как изменение радиус-вектора точки:.
Модуль перемещения совпадает с пройденным путём в том и только в том случае, если при движении направление перемещения не изменяется. При этом траекторией будет отрезок прямой. В любом другом случае, например, при криволинейном движении, из неравенства треугольника следует, что путь строго больше.
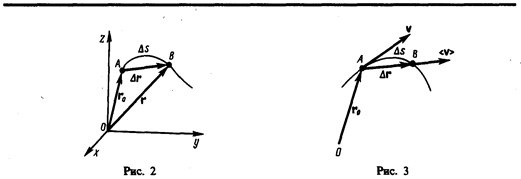
Вектор D r = r — r 0, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения |D r | равен пройденному пути D s.
Линейная скорость тела в механике
Скорость
Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.
Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r0 (рис. 3). В течение малого промежутка времени D t точка пройдет путь D s и получит элементарное (бесконечно малое) перемещение Dr.
Вектором средней скорости <v> называется отношение приращения Dr радиуса-вектора точки к промежутку времени D t:
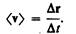(2.1)
Направление вектора средней скорости совпадает с направлением Dr. При неограниченном уменьшении D t средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:
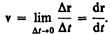
Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 3). По мере уменьшения D t путь D s все больше будет приближаться к |Dr|, поэтому модуль мгновенной скорости
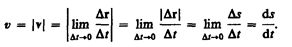
Таким образом, модуль мгновенной скорости равен первой производной пути по времени:
(2.2)
При неравномерном движении — модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной á v ñ — средней скоростью неравномерного движения:
Из рис. 3 вытекает, что á v ñ> |ávñ|, так как D s > |Dr|, и только в случае прямолинейного движения
Если выражение d s = v d t (см. формулу (2.2)) проинтегрировать по времени в пределах от t до t + D t, то найдем длину пути, пройденного точкой за время D t:
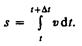(2.3)
В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (2.3) примет вид
Длина пути, пройденного точкой за промежуток времени от t 1 до t 2, дается интегралом
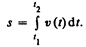
Ускорение и его составляющие
В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.
Рассмотрим плоское движение, т.е. движение, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор v задает скорость точки А в момент времени t. За время D t движущаяся точка перешла в положение В и приобрела скорость, отличную от v как по модулю, так и направлению и равную v1 = v + Dv. Перенесем вектор v1 в точку А и найдем Dv (рис. 4).
Средним ускорением неравномерного движения в интервале от t до t + D t называется векторная величина, равная отношению изменения скорости Dv к интервалу времени D t
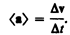
Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет предел среднего ускорения:
Таким образом, ускорение a есть векторная величина, равная первой производной скорости по времени.
Разложим вектор Dv на две составляющие. Для этого из точки А (рис. 4) по направлению скорости v отложим вектор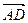 
, по модулю равный v1. Очевидно, что вектор 
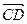, равный 
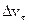, определяет изменение скорости за время D t по модулю: 
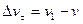. Вторая же составляющая 
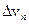вектора Dv характеризует изменение скорости за время D t по направлению.
Тангенциальное и нормальное ускорение.
Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости. Обозначается обычно или (, итд в соответствии с тем, какая буква выбрана для обозначения ускорения вообще в данном тексте).
Иногда под тангенциальным ускорением понимают проекцию вектора тангенциального ускорения — как он определен выше — на единичный вектор касательной к траектории, что совпадает с проекцией (полного) вектора ускорения на единичный вектор касательной то есть соответствующий коэффициент разложения по сопутствующему базису. В этом случае используется не векторное обозначение, а «скалярное» — как обычно для проекции или координаты вектора — 
.
Величину тангенциального ускорения - в смысле проекции вектора ускорения на единичный касательный вектор траектории - можно выразить так:
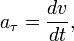
где 
- путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент.
Если использовать для единичного касательного вектора обозначение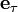 
, то можно записать тангенциальное ускорение в векторном виде:
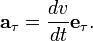
Вывод
Выражение для тангенциального ускорения можно найти, продифференцировав по времени вектор скорости, представленный в виде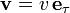 
через единичный вектор касательной 
:
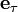где первое слагаемое — тангенциальное ускорение, а второе — нормальное ускорение.
Здесь использовано обозначение 
для единичного вектора нормали к траектории и 
- для текущей длины траектории (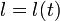
); в последнем переходе также использовано очевидное
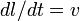
и, из геометрических соображений,
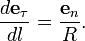
Центростремительное ускорение(нормальное) — часть полного ускорения точки, обусловленного кривизной траектории и скоростью движения по ней материальной точки. Такое ускорение направлено к центру кривизны траектории, чем и обусловлен термин. Формально и по существу термин центростремительное ускорение в целом совпадает с термином нормальное ускорение, различаясь скорее лишь стилистически (иногда исторически).
Особенно часто о центростремительном ускорении говорят, когда речь идет о равномерном движении по окружности или при движении, более или менее приближенном к этому частному случаю.
Элементарная формула
или
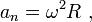
где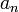 
— нормальное (центростремительное) ускорение, 
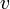— (мгновенная) линейная скорость движения по траектории, 
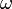— (мгновенная) угловая скорость этого движения относительно центра кривизны траектории, 
— радиус кривизны траектории в данной точке. (Cвязь между первой формулой и второй очевидна, учитывая).
Выражения выше включают абсолютные величины. Их легко записать в векторном виде, домножив на — единичный вектор от центра кривизны траектории к данной ее точки:
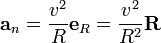
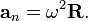
Эти формулы равно применимы к случаю движения с постоянной (по абсолютной величине) скоростью, так и к произвольному случаю. Однако во втором надо иметь в виду, что центростремительное ускорение не есть полный вектор ускорения, а лишь его составляющая, перпендикулярная траектории (или, что то же, перпендикулярная вектору мгновенной скорости); в полный же вектор ускорения тогда входит еще и тангенциальная составляющая (тангенциальное ускорение)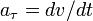 
, по направлению совпадающее с касательной к траектории (или, что то же, с мгновенной скоростью).
Вывод
То, что разложение вектора ускорения на компоненты — одну вдоль касательного к траектории вектора (тангенциальное ускорение) и другую ортогональную ему (нормальное ускорение) — может быть удобным и полезным, довольно очевидно само по себе. Это усугубляется тем, что при движении с постоянной по величине скоростью тангенциальная составляющая будет равной нулю, то есть в этом важном частном случае остается только нормальная составляющая. Кроме того, как можно увидеть ниже, каждая из этих составляющих имеет ярко выраженные собственные свойства и структуру, и нормальное ускорение содержит в структуре своей формулы достаточно важное и нетривиальное геометрическое наполнение. Не говоря уже о важном частном случае движения по окружности (который, к тому же, практически без изменения может быть обобщен и на общий случай).
Формальный вывод
Разложение ускорения на тангенциальную и нормальную компоненты (вторая из которых и есть центростремительное или нормальное ускорение) можно найти, продифференцировав по времени вектор скорости, представленнный в виде 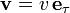через единичный вектор касательной 
.
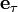Где первое слагаемое — тангенциальное ускорение, а второе — нормальное ускорение.
Здесь использовано обозначение 
для единичного вектора нормали к траектории и — 
для
текущей длины траектории (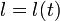); в последнем переходе также использовано очевидное
.
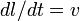Далее можно просто формально назвать член
— нормальным (центростремительным) ускорением. При этом его смысл, смысл входящих в него объектов, а также доказательство того факта, что он действительно ортогонален касательному вектору (то есть что — действительно вектор нормали) — будет следовать из геометрических соображений (впрочем, то, что производная любого вектора постоянной длины по времени перпендикулярна самому этому вектору, — достаточно простой факт; в данном случае мы применяем это утверждение для).
