Основы теории
Расчет гидравлических сопротивлений при движении реальных жидкостей и газов по трубам является одной из основных задач гидрогазодинамики. Для определения движущей силы гидродинамических процессов - разности давлений между двумя точками или сечениями потока - необходимо знать потери напора h или давления ∆Р. Важность определения потерь связана с необходимостью расчета затрат энергии при перемещении жидкостей или газов с помощью насосов, компрессоров и другого оборудования. Потери в трубопроводах обусловливаются как наличием вязкостного внутреннего трения по длине трубы, так и местными сопротивлениями.
Сопротивление трения существует при движении реальной жидкости по
всей длине трубопровода. На него влияют режим течения жидкости (ламинарный, турбулентный), а также степень развития турбулентности при турбулентном режиме. В случае ламинарного движения жидкости по прямой трубе потеря напора на трение h может быть определена теоретически на основании уравнения Пуазейля.
Согласно уравнению Бернулли для горизонтального трубопровода (z1=z2) постоянного сечения напор, теряемый на трение, равен:
(5.1)
т.е. потеря напора по длине равна уменьшению удельной потенциальной энергии (гидростатического напора) потока и выражается перепадом пьезометрических уровней в начальном конечном сечениях участка трубопровода. Так как потер обусловлены вязкостью жидкости, теряемая энергия потока рассеивается и переходит в теплоту. Потеря напора на преодоление трения при движении
потока в круглой цилиндрической трубе описывается эмпирической формулой
Дарси - Вейсбаха:
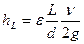(5.2)
или для потери давления ∆Р (с учетом того, что 
)
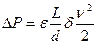(5.3)
где ε – безразмерный коэффициент гидравлического сопротивления (коэффициент трения); L и d – соответственно длина и диаметр трубы; ρ – плотность жидкости или газа; υ – средняя скорость потока.
Из формулы (5.3) и (5.2) следует, что потеря давления на трение пропорциональна скоростному или динамическому давлению 
которое является мерой кинетической энергии потока, отнесенной к единиц» объема жидкости. При этом коэффициент ε показывает, во сколько раз напор, потерянный на трение, отличается от скоростного напора.
Коэффициент трения в общем случае зависит от характера движения жидкости (т.е. от критерия Рейнольдса) и от степени шероховатости стенок трубопро-вода:
(5.4)
где 
- относительная гладкость трубы.
1.При ламинарном течении (Rе < 2320) коэффициент трения практически не зависит от шероховатости стенок трубопровода и определяется как
(5.5)
Для каналов некруглого сечения вместо диаметра d подставляют эквивалентный диаметр dэ:
(5.6)
где S – площадь поперечного сечения трубопровода; П – его «смоченный периметр».
При изотермическом ламинарном течении газов и жидкостей потери давления на трение могут быть рассчитаны по формуле Гагена –Пуазейля
(5.7)
где μ – динамический коэффициент вязкости
2.При турбулентном течении выражение для коэффициента трения не может быть выведено теоретически из-за сложности структуры турбулентного потока. Поэтому расчетные соотношения получают обобщением результатов опытов методом теории подобия.
Зона гидравлических гладких труб (рис.5.1,а). Как было указано выше,
коэффициент трения зависит от степени шероховатости стенки трубы. Шерохова-тость не оказывает влияния на коэффициент трения при ламинарном и переходном режимах. Даже после того как течение станет турбулентным, числа Rе еще не велики, влияние шероховатости незначительно. Это происходит потому, что вязкий подслой, толщина которого уменьшается с ростом Rе, перекрывает высгупы, создающие шероховатость Δ, и в этим режиме трубопроводы можно рассматривать как гидравлически гладкие.
Чаще всего этой зоне соответствует течете в стеклянных, медных и других гладких трубах. В этой зоне 
и его расчет ведут по формуле Блазиуса:
(5.8)
Формула (5.8) справедлива при Re <1000. Потери напора в этой зоне hL пропорциональны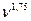 
Зона гидравлически шероховатых труб (стальных, чугунных, рис.5.1,б). С увеличением числа Rе толщина вязкого подслоя δ уменьшается. Он уже не перекрывает выступы стенок трубы, и коэффициент трения становится зависимым как от Rе, так и от Δ. Вокруг выступов возникают дополнительные вихри.
Эта область течения наблюдается при
(5.9)
Автомодельная область (рис.5.1,в). При дальнейшем увеличении числа
(Rе > 500d/Δ) возникает автомодельная по отношению к Rе область. Скорость у стенки возрастает настолько, что толщина вязкого подслоя становится намного меньше степени шероховатости (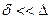
). При этом скорость, а следовательно, и потеря напора на трение возрастают под действием сил инерции, возникающих вследствие дополнительного вихреобразования вокруг выступов, создающих шероховатость, практически перестают зависеть от критерия Рейнольдса и определяются лишь степенью шероховатостью стенок труб 
. Автомодельную область называют также областью квадратичного закона сопротивления, так как согласно уравнению (5.3) при отсутствии влияния Rе на величину ε сопротивление трения становится пропорциональным квадрату скорости d. Коэффициент ε рассчитывают по формуле (5.9), которую, пренебрегая вторым слагаемым в квадратных скобках, приводят к виду
(5.10)
Графики зависимости ε от Re и шероховатости представлены на рис.5.2.
На коротких участках трубопровода резко изменяется конфигурация потока и возникают местные гидравлические сопротивления. Изменение конфигурации может быть вызвано наличием расширений, сужений, поворотов, установкой регулирующей арматуры (кранов, вентилей, клапанов) и др. Местные сопротивления вызывают вихреобразование, турбулизацию потока, что приводит к потерям энергии и напора, называемых местными потерями hм.
Рис.5.2
На рис.5.3 показано резкое сужение потока. Пьезометрическая линяя на этом рисунке характеризует изменение пьезометрического напора по длине участка.
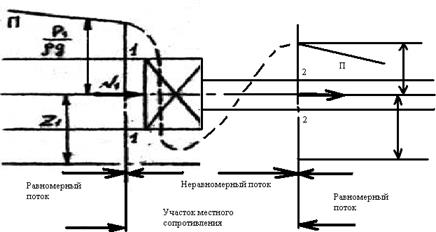
Рис.5.3
Для расчета местных потерь напора применяется формула Вейсбаха, выражающая потери в долях скоростного напора:
(5.11)
где ξ – коэффициент местного сопротивления.
Значения ξ определяется типом местного сопротивления и числом Rе.
Обычно местные сопротивления наблюдаются в условиях автомодельности по
числу Rе, так как турбулизация потока возникает уже при низких числах Rе.
Экспериментальные значения ξ для основных типов местных сопротивлений
приведены в приложении 3.
Описание установки
Для определения потерь напора и коэффициентов гидравлических сопро- тивлений на лабораторной установке используется трубопровод 7 (рис.5.4) переменного сечения, причем для определения гидравлических потерь напора по длине и коэффициентов сопротивления трения используют участки трубопровода 1-2 и 5-8, а для определения коэффициентов местных сопротивлений (в колене, при резком расширении и сужении сечения трубы) - участок 2-12. Маркировка участков трубопровода произведена по имеющимся на нем фланцам, в которых установлены штуцера отбора, последовательно соединенные резиновыми трубками 6 с соответствующими пьезометрами 5. Пьезометры укреплены на панели установки и снабжены шкалами для измерения уровней подъема жидкостей в них.
Участок трубопровода 1-2 имеет длину L = 1,0 м, внутренний диаметр d = 0,01 м; участок 5-8 - длину L = 0,6 м, внутренний диаметр d = 0,021 м. Рабочая жидкость подается в трубопровод 7 из напорного резервуара 11, в который она нагнетается центробежным насосом 10 при открытом кране К1 из сварного бака 1.
С передней стороны напорный резервуар 12 закрыт прозрачной стенкой, которая позволяет наблюдать за уровнем жидкости. Этот уровень поддерживается постоянным с помощью сливной трубы, через которую избыточная жидкость сливается в бак 1. Постоянство напора в резервуаре 3 позволяет установить нужный режим движения жидкости в трубопроводе. Расход жидкости в трубопроводе 7 регулируется поворотом крана К2. Определение расхода жидкости производится с помощью мерного резервуара, установленного на выходе из трубопровода, при закрытом кране К3 по шкале уровня подъема жидкости 8 и тарировочному графику. При открытом кране КЗ жидкость через трубопровод и мерный резервуар сливается в бак 9.
Включение и выключение установки производится тумблером 2. В течение опыта кран К1 остается отрытым.
Рис.5.4
Порядок выполнения работы
1 Включить насос тумблером 2 и, регулируя подачу жидкости краном К1, наполнить напорный резервуар 3 до уровня сливной трубы 4 (в течение опыта насос остается включенным).
2.Установив краном К2 определенный режим движения жидкости по трубо-проводу 7, закрыть кран КЗ и заполнить мерный резервуар, измеряя время его заполнения τ. Определить объем жидкости V, используя измерительную шкалу 8 и тарировочный график.
3.Определить расход жидкости, перемещаемой по трубопроводу 7, по формуле 
.
4.При установившемся движении жидкости снять показания пьезометров 5 (h1 – h10).Результаты измерений записать в таблицу.
5.Выполнить измерения при других расходах, повторив пп.2...4.
6. Измерить температуру воды в резервуаре.
Обработка экспериментальных данных
1. Рассчитать средние скорости в трубопроводе 
для узкого и широкого сечений.
2. Определить опытные потеря напора на исследуемых участках трубопровода
3. Рассчитать опытные коэффициенты ε и ξ для найденных потерь напора по формулам (5.2) и (5.11) соответственно.
4. Определить кинематическую вязкость воды по приложению 2 в соответствии с ее измеренной температурой.
5. Рассчитать число Рейнольдса для узкого и широкого сечений трубы по формуле 
6.Определить зону гидравлического сопротивления, выбрать соответствующую ей формулу для расчета ε и произвести расчет.
7.По приложению 3 найти табличные значения используемых в работе коэффи-циентов местных сопротивлений.
8.Сравнить опытные коэффициенты ε и ξ с теоретическими, оценить ошибки и все результаты вычислений внести в таблицу.
9.Построить график зависимости опытных коэффициентов трения ε от числа Рейнольдса и обозначить зоны гидравлического сопротивления.
| Измеряемая величина | Опыт | |||
| 1 | 2 | 3 | 4 | |
| Показания водяного пьезометра, м.вод.ст | ||||
| h1 | ||||
| h2 | ||||
| Объём жидкости Q, м3 | ||||
| Время опыта τ, с | ||||
| Площадь живого сечения S, м2 | ||||
| Расчётные величины для определения потерь по длине трубопровода | ||||
| Расход жидкости V, м3/с | ||||
| Средняя скорость υ, м/с, на участке | ||||
| узком | ||||
| широком | ||||
| Опытный коэффициент трения ε | ||||
| Число Рейнольдса Rе | ||||
| Теоретический коэффициент трения εТ | ||||
| Теоретические потери напора по длине hT |
