Основы теории.
Уравнение Бернулли является одним из основных уравнений гидрогазодинамики. Оно получается при интегрировании дифференциальных уравнений движения идеальной жидкости Эйлера и используется при решении многих задач движения газов и жидкостей.
В лабораторной работе применяется одна принятая в литературе как
основная форма уравнения Бернулли для установившегося потока несжимаемой
жидкости, когда из массовых сил на жидкость действует только сила тяжести.
Для струйки реальной несжимаемой жидкости, проходящей между двумя сече-
ниями 1-1 и (рис.4.1) 2-2, уравнение Бернулли, имеет вид
(4.1)
Рис.4.1
Входящие в уравнение слагаемые можно интерпретировать с энергетичес- кой и геометрической точек зрения.
С энергетической точки зрения выражение (4.1) представляет собой частный случай закона сохранения энергии; сумма удельных (отнесенных к единице веса), кинетической и потенциальной энергий остается постоянной вдоль всей струйки.
Здесь z - удельная энергия положения в рассматриваемом сечении;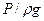 
- удельная энергия давления в том же сечении; 
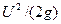- удельная кинетическая энергия в том же сечении; 
- удельная потенциальная энергия; 
- полная удельная энергия струйки жидкости; hп – потери удельной энергии в интервале между рассматриваемыми сечениями, связанные с работой сил вязкостного трения, действующих в реальной жидкости.
С геометрической точки зрения z – высота положения сечения,или расстояние от центра тяжести рассматриваемого живого сечения до плоскости сравнения 0-0, которая выбирается произвольно; 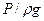- пьезометрическая высота, или высота столба жидкости плотности ρ, который у своего основания создает давление Р, равное давлению в данном сечении; 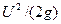- скоростной напор, или высота, с которой должно упасть тело единичной массы, чтобы в конце пути приобрести скорость U (обозначается h ск); - гидродинами-ческий или полный напор, равный сумме трех рассмотренных выше высот; hп – потери напора между сечениями 1-1 и 2-2, связанные с наличием сил вязкости в потоке.
Индексы 1 и 2 в уравнении (4.1) указывают соответствующее данному параметру сечение. Таким образом, давление Бернулли свидетельствует о том, что по длине струйки реальной жидкости гидродинамический напор (равно как и полная удельная энергия) уменьшается.
Перейдя к рассмотрению уравнения Бернулли для целого потока реальной жидкости, необходимо отметить, что локальные скорости потока, состоящего из множества элементарных струек, неодинаковы. Распределение этих скоростей подчиняется определенным законам. Скорости изменяются от нуля у стенки до максимального значения Umax в центре потока. Удельная кинетическая энергия потока равна сумме удельных кинетических энергий отдельных струек по всему сечению. Кинетическая энергия, вычисленная по средней скорости в данном сечении 
(где V - объемный расход, а S - площадь сечения), не равна кинетической энергии, вычисленной по сумме энергий всех элементарных струек. Для обеспечения равенства вводится коэффициент α, называемый коэффициентом Кориолиса. С учетом сказанного скоростной напор
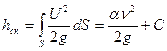(4.2)
Коэффициент Кориолиса зависит от того, как распределены скорости по сечению потока. При ламинарном течении в круглой трубе, например, α =2, а при развитом турбулентном течении α= 1,05... 1,15. С учетом отмеченных особен-ностей уравнение Бернулли для потока реальной жидкости имеет вид
(4.3)
В этом уравнении все члены имеют тот же смысл, что и члены уравнения Бернулли для струйки реальной жидкости.
Относительные изменения параметров уравнения Бернулли по длине трубы имеют свои названия. Так, изменение z по длине называется геометрическим уклоном 
.Величина
называется пьезометрическим уклоном и показывает изменение пьезометрического напора по длине, а величина
называется гидравлическим уклоном.
Для большинства практических расчетов можно принять α = 1. Тогда уравнение (4.3) приобретет вид (4.1) с той разницей, что вместо локальной скорости U использована средняя скорость υ.
Для построения диаграммы уравнения Бернулли от произвольной точки плоскости 0-0 откладываем вверх значения z для каждого сечения и получаем линию оси потока. Затем от оси откладываем вверх соответствующие пьезометрические высоты 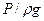и получаем пьезометрическую линию потока. Отложив далее вверх доя каждого сечения значения скоростного напора h ск, получим линию полного напора. Разность между полными напорами двух сечений дает величину потерь напора hп.
Описание установки.
Основной частью лабораторной установки (рис.4.2) является наклонно
закрепленный на передней панели трубопровод 7 переменного сечения. Вода по
ступает в трубопровод из напорного бака 2, куда она нагнетается центробежным насосом 10 из резервуара 9. Постоянный уровень в напорном баке поддерживается с помощью сливного устройства 1. Скорость воды в трубопроводе регулируется краном 8. Через него осуществляется слив воды в резервуар 9, служащий основанием установки.
По длине трубопровода 7 выделено пять характерных сечений, различающихся до форме и размерам. В каждом из них установлено по две трубки: левая 3 пьезометрическая (трубка Прандтля) и правая 4 с загнутым навстречу потока концом (трубка Пито). Трубки имеют шкалы для определения уровня подъема
в них вода. Вдоль трубок установлено два ряда подвижных кареток (верхний 5 -
и нижний 6) с протянутыми через них нитями. С помощью кареток фиксируются показания уровней воды в трубках. Для определения геометрической высоты
центров выделенных сечений трубопровода установлены линейки. При этом за
плоскость сравнения принята плоскость крышки резервуара 9. Геометрические
координаты сечений следующие: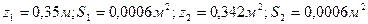 
Расстояние между сечениями 1-2 и 4-5 190 мм, а между сечениями 2-3 и 3-4 120 мм.
Включение и выключение центробежного насоса осуществляется тумблером, расположенным на передней панели установки.
Порядок выполнения работы
1.Перед началом работы перекрыть кран 5 для заполнения системы.
2.Включить вилку в сеть и поставить тумблер центробежного насоса в
верхнее положение. Насос должен оставаться включенным в течение всех опытов. Избыток воды сливается из напорного бака в сливное устройство 1, обеспечивая постоянный напор в трубопроводе 7.
3.Открыв кран 8, установить заданный расход воды в трубопроводе 7 и в течение опыта поддерживать этот расход постоянным.
4.Для пяти сечений трубопровода в таблице записать: геометрические напоры z (нивелирные высоты), по показаниям пьезометров – пьезометрические высоты 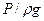и по показаниям трубок Пито – Прандтля – значения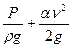 
5.3афиксировать с помощью подвижных кареток 5 и 6 положения нитей пьезометрической линии, лини полного напора и зарисовать их.
6. Измерить термометром температуру воды, циркулирующей в системе.
7. С помощью регулировочного крана 8 установить новый расход воды.
8. Повторить действия, указанные в пп.4...6. Результаты занести в таблицу.
9.Сравнить положение пьезометрической линии и линии полного напора с их положением в предыдущем опыте.
Опыт
| Номер сечения | z, м | Измерено, м | Вычислено | ||||||
|
|
| 
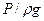
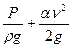
| hi | hск | υ, м/с | Re | α | ||
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| hп =∑hi = |
Опыт
| Номер сечения | z, м | Измерено, м | Вычислено | ||||||
|
|
|
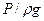
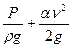
| hi | hск | υ, м/с | Re | α | ||
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| hп =∑hi = |
Обработка экспериментальных данных.
1.Определить и записать в таблицу для каждого из рассмотренных сечений значения составляющих полного напора
2.По уравнению (4.3) определить hi - потери напора между соседними сечениями трубопровода (четыре значения) и записать в таблицу.
3.Вычислить потери напора hп по всей длине трубопровода между сечениями 4-5. Эта величина должна равняться сумме потерь на отдельных участках:
4.По данным таблицы с учетом сделанных зарисовок пьезометрической
линии и линии полного напора построить диаграмму уравнения Бернулли для двух опытов.
5. По тарировочному графику, зная перепад пьезометрических высот между сечениями 1-5, определить объемный расход воды V, м3/с.
6. Рассчитать средние скорости для широкого и узкого сечений по формуле
7.По приложению 2 с учетом измеренной температуры воды найти кине-матическую вязкость и рассчитать значения критерия Рейнольдса по формуле
8.3ная среднюю скорость υ и скоростной напор, определить коэффициенты
α в каждом сечении.
9.Полученные данные для обоих опытов занести в таблицу.
10.Построить график зависимости коэффициента α от Re для всех полученных значений.
В выводах о работе необходимо объяснить геометрический и энергетический смысл членов уравнения Бернулли, вид перехода одного вида энергии в другой, причины изменения характера пьезометрической линии и линии гидро-динамического напора по всей длине трубопровода. Следует также объяснить физический смысл коэффициента Кориолиса и указать, как влияет на его значение режим течения жидкости.
