Порядок выполнения работы. Параметры жидкости, как в неподвижном, так и в равномерно вращающемся сосуде описываются уравнениями гидростатики

Основы теории

Параметры жидкости, как в неподвижном, так и в равномерно вращающемся сосуде описываются уравнениями гидростатики, так как частицы неподвижны относительно друг друга и стенок сосуда и жидкость ведет себя как твердое тело.

Для нахождения уравнения свободной поверхности жидкости воспользу­емся выражением полного дифференциала давления, полученного из уравнений гидростатики Эйлера:

 

(2.1)

 

Для поверхностей равного давления полный дифференциал давления ра­вен нулю. Тогда из уравнения (2.1) подучим

 

(2.2)

 

Если сосуд неподвижен, массовой силой является только сила тяжести, удельным значением которой является ускорение свободного падения g, про­екти- рующееся только на ось z.В этом случае x=y=0 и z=-g Тогда согласно уравнению (2.1) получим:

 

 

а проинтегрировав –

 

(2.3)

 

где Р₀- давление на поверхности жидкости.

Проинтегрировав при тех же условиях уравнение (2.2), получим z=const. Таким образом, в неподвижной жидкости распределение давления по высоте описывается линейной зависимостью, а поверхности равного давления пред­ставляют собой горизонтальные плоскости.

Если сосуд находится в состоянии равномерного вращения вокруг верти­кальной оси, на жидкость кроме силы тяжести действует еще центробежная сила. Она действует перпендикулярно оси вращения, поэтому проектируется только на оси x и y. Удельными значениями проекций центробежной силы на оси координат являются проекции ее ускорения

 

 

на ось x

на ось y

где ω - частота вращения сосуда.

Интегрирование уравнения (2.1) в этом случае дает закон распределения давления в жидкости:

 

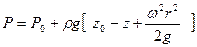(2.4)

 

Подставив значения Х,Y я Z в уравнение (2.2), после интегрирования с учетом того, что , получим:

 

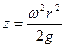(2.5)

 

Это уравнение описывает параболоид вращения с центром координат в его вершине. Расстояние от поверхности неподвижной жидкости до его вершины (рис.2.1) определяется по формуле

 

(2.6)

 

а координата его верхней кромки

 

(2.7)

 

т.е.

Рис.2.1

Как показало на рис.2.1, при вращении сосуда часть жидкости в центре сосуда, находящаяся ниже уровня неподвижного слоя, вытесняется вверх. Объ­ем вытесненной части равен объему параболоида вращении от его вершины до уровня

 

(2.8)

 

где - площадь произвольного кругового сечения параболоида, записанная с учетом уравнения (2.5).Рассмотренный объем вытесняется в зону, расположенную выше уровня неподвижного слоя, и представляет собой разность объемов цилиндра с радиусом R и высотой z_в – z_н и усеченного параболоида той же высоты:

 

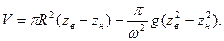(2.9)

 

Описание установки

Лабораторная установка (рнс.2.2) представляет собой цилиндрически со­суд 7 диаметром 160 мм, заполненный примерно до половины трансформатор­ным маслом. Сосуд приводится во вращение электродвигателем через червяч­ный редуктор, установленный в корпусе 8. Частота вращения сосуда изменяется в опытах с помощью регулятора 11, измеряетеся тахометром и может быть ус­тановлена в диапазоне 0...200 мин¹. Частота вращения измеряется по шкале 9, имеющейся на передней панели прибора.

 

Рис.2.2

 

Для определения горизонтальных и вертикальных координат свободной поверхности жидкости в сосуде имеется измерительная игла 6, связанная с кареткой 3, позволяющей перемещать иглу в горизонтальном направлении руко­яткой 4. В вертикальном направлении игла перемещается по пазу, имеющемуся в каретке, с помощью рукоятки 2. Положение иглы относительно выбранного центра отсчета определяется по горизонтальной 5 и вертикальной 1 шкалам. Горизонтальная шкала неподвижно укреплена на корпусе установки, а вертикальная - на держателе иглы. Точность измерения высоты положения иглы может быть повышена с помощью шкалы нониуса, нанесенной на корпус держателя иглы. Для освещения прибора используется электрическая лампочка, включение которой осуществляется тумблером 10. На схеме установки штрихами изображены положение свободной поверхности, описываемой параболоидом вращения, и ее координаты y и z.

Порядок выполнения работы.

1.Убедиться, что регулятор частоты вращения 11 находится в крайнем ле­вом положении. Включить тумблер 10 электрического освещения и измерить иглой высоту неподвижной поверхности жидкости h_н.

2.Регулятором 11 по шкале тахометра 9 установить заданную преподавате­лем частоту вращения и поддерживать ее постоянной в процессе работы путем плавной корректировки.

З.После того как в сосуде установится стабильная форма поверхности жидкости (через 2...3 мин), можно начать определение координат свободной поверхности жидкости. Для этого, поместив иглу в центр, опустит ее вниз до соприкосновения с поверхностью жидкости и определить по шкале 1 верти­кальную координату вершины параболоида h_н. Аналогично поступить при из­мерении других координат при соответствующих радиусах r. При каждом из­мерении иглу сначала поднять выше уровня жидкости, рукояткой 4 перемес­тить ее на расстояние r сначала влево и измерить координату h’, а затем вправо для измерения координаты h’’. Результаты измерений занести в таблицу.

4.3атем провести вторую серию опытов при другой заданной частоте вра­щения в той же последовательности.

5.По окончании работ снизить частоту вращения до нуля, выключить электро-двигатель и лампу и, вернуть каретку в исходное положение.