Проинтегрируем выражения для плотности активного потока энергии по площади поперечного сечения волновода:
, ВА (11)
Параграф № 11
Определение фазовой скорости Vф и скорости распространения энергии Vэ рассматриваемой волны. Рассчитаем и построим графики зависимостей Vф и Vэ от частоты.
За время 
волна распространяется на расстояние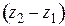 
, при этом фазы волны в моменты времен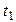и 
и 
в плоскостях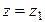 
и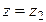 
сответственно совпадают.
здесь 
– фаза в момент времени t=0.
Рассчитаем фазовую скорость волны с учетом 
м.
, м/с
Для расчета скорость распространения энергии Vэ воспользуемся соотношением:
Vэ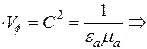 
Vэ 
, м/с.
Запишем выражение, характеризующее зависимость фазовой скорости от длины волны в волноводе.
Vэ 
, м/с.
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики зависимостей Vф и Vэ от частоты. Результаты показаны на Рис. 18.
Параграф № 12
Определить коэффициент затухания для заданной волны, считая, что стенки трубы выполнены из реального металла имеющего Сим/м, на основе граничных условий Леонтовича-Щукина.
Формула для расчета коэффициента затухания на основе граничных условий Леонтовича-Щукина имеет вид [1]:
,
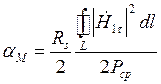где 
,
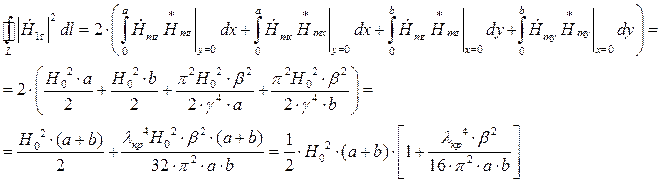
Раскроем частотную зависимость коэффициента затухания:
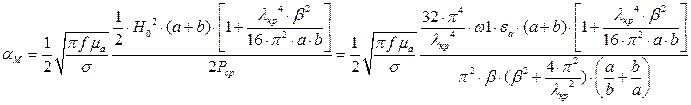
Выражение для Рср подставлено из параграфа 8 для случая, когда частота принадлежит найденному в параграфе 2 диапазону.
Сделав замену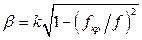 
и подставив 
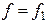в полученное выражение для коэффициента затухания, получим:
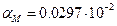, Нп/м
Параграф № 13
Рассчитать и построить график зависимости коэффициента затухания волны в волноводе от частоты.
, Нп/м
Указанная формула была запрограммированы в математическом пакете MathCAD 14, где был график зависимости 
. Результаты показаны на Рис. 19
График представлен в логарифмическом масштабе для того, чтобы показать наглядно различающиеся величины.
Параграф № 14
Определить тип волны, распространяющейся в волноводе. Изобразить структуру силовых линий электрического и магнитного полей этой волны и плотности поверхностного тока проводимости, протекающего по стенкам волновода.
Данная волна является волной типа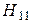 
, так как только вектор 
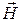имеет продольную составляющую и вдоль каждой стенки волновода укладывается одна полуволна по осям Х и У соответственно.
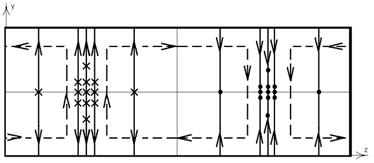
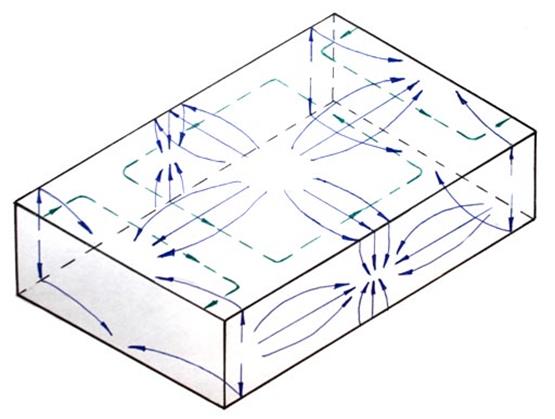
Структура силовых линий электрического и магнитного полей этой волны (Рис. 20) и плотности поверхностного тока проводимости, протекающего по стенкам волновода (Рис 21).
 |
Рис. 18
 |
Рис. 19
 | ||||
 | ||||
 |
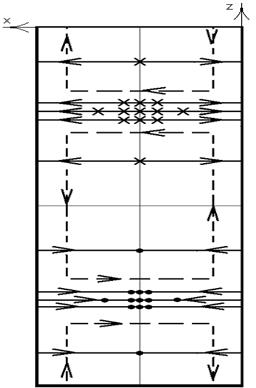Рис. 20
 |
 |
Рис. 21
Вывод:
Результатом работы стало исследование волны в прямоугольном волноводе. По заданным соотношениям были определены все составляющие обоих векторов электромагнитного поля. Исследованы зависимости амплитуд составляющих поля от координат в режиме бегущей волны и в режиме стоячей волны. На графиках показано экспоненциальное затухание волны с ростом координаты z в режиме стоячей волны и неизменность амплитуды ее колебаний при изменении координаты z в режиме бегущей волны (без учета потерь). В ходе исследования установлено, что рассматриваемая волна относится к типу Н11. Проверено выполнение граничных условий для касательных составляющих вектора 
и нормальной составляющей вектора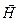 
на стенках волновода. Получены выражения для поверхностных токов и зарядов на стенках волновода. Найден вектор Пойтинга в комплексной форме и в форме мгновенного значения. Определено среднее за период значение плотности потока энергии, проходящей через поперечное сечение волновода. Определены и рассчитаны фазовая скорость и скорость распространения энергии волны в волноводе, зависимости фазовой скорости и скорости распространения энергии построены графически. Рассчитан коэффициент затухания волны при использовании волновода из реального металла с заданной проводимостью, зависимость коэффициента затухания от частоты построена графически. Структура силовых линий электрического и магнитного полей, а также структура силовых линий плотности поверхностного тока проводимости изображены на соответствующих рисунках.
Математические расчёты совпадают с построенными графическими зависимостями
Использованная литература:
[1]-Техническая электродинамика / Пименов Ю.В., Вольман В.И., Муравцов А.Д. Под ред. Ю.В. Пименова: Учебное пособие для вузов. – М.: Радио и связь, 2002.
[2]-Электромагнитные волны/ Вайнштейн. Л. А. – М.: Радио и связь, 1988.
