Комплексную амплитуду поверхностного тока можно найти по формуле:
(25)
Комплексную амплитуду плотности зарядов можно найти по формуле:
(26)
Найдем комплексные амплитуды плотностей поверхностных токов и зарядов на всех стенках трубы:
1) Для нижней стенки трубы 
нормаль совпадает с вектором 
: 
.
Касательными к этой стенке составляющими вектора 
являются составляющие вдоль осей x и z, то есть:
Подставим это выражение в формулу (25):
Нормальной к этой стенке составляющей вектора 
будет составляющая 
. Тогда комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
2) Для верхней стенки трубы 
нормаль противоположна вектору : 
.
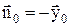Касательными к этой стенке составляющими вектора являются составляющие вдоль осей x и z, то есть:
Подставим это выражение в формулу (25):
Нормальной к этой стенке составляющей вектора будет составляющая . Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
3) Для правой стенки трубы 
нормаль совпадает с вектором 
: 
.
Касательными к этой стенке составляющими вектора являются составляющие вдоль осей y и z, то есть:
Подставим это выражение в формулу (25):
Нормальной к этой стенке составляющей вектора будет составляющая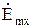 
. Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
4) Для левой стенки трубы 
нормаль противоположна вектору : 
.
Касательными к этой стенке составляющими вектора , как и в третьем случае, являются составляющие вдоль осей y и z, то есть:
Подставим это выражение в формулу (25):
Нормальной к этой стенке составляющей вектора будет составляющая 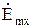. Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
Комплексные амплитуды поверхностных токов и зарядов на всех стенках трубы показаны на Рис. 14, Рис. 15, Рис. 16. Рис. 17
Нижняя стенка (y = 0) Рис. 14
Верхняя стенка (y = b) Рис. 15
Правая стенка (x =0) Рис. 15
Левая стенка (x =a) Рис. 16
Параграф № 8
Записать выражение для комплексного вектора Пойтинга для двух случаев: когда частота принадлежит найденному в п. 2 диапазону и когда она не принадлежит этому диапазону. Определить среднее за период значение плотности потока энергии и амплитуду плотности реактивного потока энергии.
Рассмотрим режим бегущей волны 
:
Запишем выражения для сопряженных составляющих вектора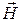 
:
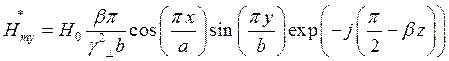
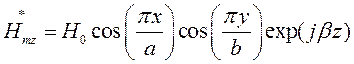
Найдём выражения для каждой из составляющих вектора Пойтинга, исходя из (27):
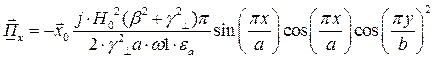
Тогда выражение для вектора Пойтинга примет вид:
Cоставляющие по оси х и по оси у чисто мнимые, а составляющая по оси z – действительная, значит вдоль оси z происходит перенос энергии. Следовательно:
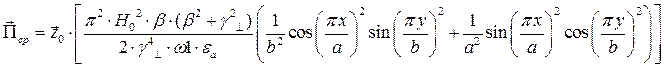
Рассмотрим режим стоячей волны 
:
Запишем выражения для сопряженных составляющих вектора :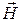
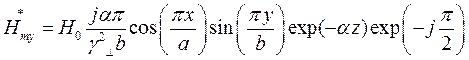
Найдём выражения для каждой из составляющих вектора Пойтинга, исходя из (27):
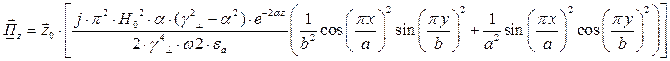
В этом случае вектор Пойтинга чисто мнимый и переноса энергии не происходит.
Параграф № 10
