5.
6.
1. Вычислить с заданной точностью значение числа 
, используя следующее разложение в ряд:
Сравните вычисленное значение со стандартным значением PI, возвращаемым классом Math. Для разных значений 
вычислите n - число членов суммы, требуемых для достижения заданной точности.
2. Вычислить с заданной точностью значение числа , используя следующее разложение в ряд:
Сравните вычисленное значение со стандартным значением PI, возвращаемым классом Math. Для разных значений вычислите n - число членов суммы, требуемых для достижения заданной точности.
3. Вычислить с заданной точностью значение числа , используя следующее разложение в ряд:
Предварительно следует записать рекуррентное соотношение для текущего члена суммы. Сравните вычисленное значение со стандартным значением PI, возвращаемым классом Math. Для разных значений вычислите n - число членов суммы, требуемых для достижения заданной точности.
4. Вычислить с заданной точностью значение числа e, используя следующее разложение в ряд:
Предварительно следует записать рекуррентное соотношение для текущего члена суммы. Сравните вычисленное значение e со стандартным значением E, возвращаемым классом Math. Для разных значений вычислите n - число членов суммы, требуемых для достижения заданной точности.
5. Дано вещественное число x. Вычислить с заданной точностью 
:
Указание: для ускорения вычислений используйте разложение в ряд только для дробной части числа x. Используйте умножение и константу e для вычисления 
, где n - это целая часть числа x.
6. Дано вещественное число x. Вычислить с заданной точностью sin(x):
Указание: для ускорения вычислений используйте разложение в ряд только для приведенного значения числа x. Помните, что sin(x) - это периодическая функция, так что всегда можно привести x к интервалу 
.
7. Дано вещественное число x, такое, что |x| <1. Вычислить с заданной точностью arcsin(x):
8. Дано вещественное число x. Вычислить с заданной точностью cos(x):
Указание: для ускорения вычислений используйте разложение в ряд только для приведенного значения числа x. Помните, что cos(x) - это периодическая функция, так что всегда можно привести x к интервалу .
9. Дано вещественное число x, такое, что |x| <1. Вычислить с заданной точностью arccos(x):
10. Дано вещественное число x >0. Вычислить с заданной точностью ln(x):
11. Дано вещественное число 0 < x < 2. Вычислить с заданной точностью ln(x):
12. Дано вещественное число x. Вычислить с заданной точностью tg(x):
где 
определяются следующим соотношением:
Указание: используйте разложение в ряд только для приведенного значения числа x. Помните, что tg(x) - это периодическая функция, так что всегда можно привести x к интервалу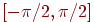 
.
13. Дано вещественное число x. Вычислить с заданной точностью arctg(x):
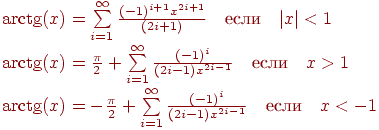
14. Дано вещественное число x. Вычислить с заданной точностью ctg(x):
где определяются следующим соотношением:
Указание: используйте разложение в ряд только для приведенного значения числа x. Помните, что сtg(x) - это периодическая функция, так что всегда можно привести x к интервалу .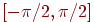
15. Дано вещественное число x. Вычислить с заданной точностью arcсtg(x):
16. Дано вещественное число x. Вычислить с заданной точностью sc(x):
где 
определяются следующим соотношением:
Указание: используйте разложение в ряд только для приведенного значения числа x. Помните, что sc(x) - это периодическая функция, так что всегда можно привести x к интервалу .
17. Дано вещественное число x. Вычислить с заданной точностью sh(x):
Указание: гиперболический синус sh(x) не является периодической функцией, поэтому никакого приведения x выполнять не следует.
18. Дано вещественное число x. Вычислить с заданной точностью ch(x):
Указание: гиперболический косинус ch(x) не является периодической функцией, поэтому никакого приведения x выполнять не следует.
19. Дано вещественное число x. Вычислить с заданной точностью Arcsh(x):
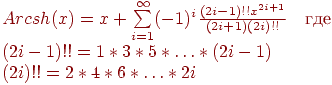
Практикум
Создайте в Visual Studio новое решение с именем Ch5_fio, где fio – это Ваша фамилия. Добавьте в созданное решение проект типа приложение Windows Forms с именем WindowsCircle и напишите программу для выполнения заданий (требуется выполнить по одному заданию из п.4,5,6 по выбору преподавателя).
Интерфейс пользователя
Для реализации диалога с пользователем используйте форму с тремя вкладками. Надпись в заголовке формы может быть такая: «Вычисление сумм и произведений». Придумайте соответствующие решаемым задачам названия для ярлычков вкладок. На каждой вкладке формы разместите поля для ввода и вывода данных, соответствующих одной из трех задач и условие задачи.
Функции отклика. Для запуска процедуры вычисления сумм или произведений на каждую вкладку добавьте управляющую кнопку (button). Код вычисления значения суммы добавляется в функции отклика на щелчок мыши по управляющей кнопке.
